11.30BST理解，AVL树操作，定义；快速幂，二分求矩阵幂（未完）

完全二叉树结点的度可能有1，满二叉树的度只能为0或2

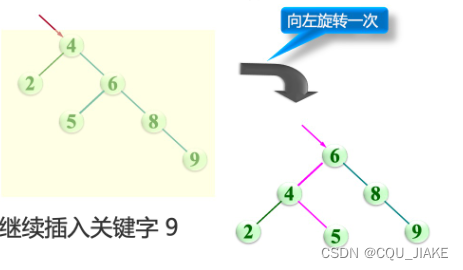
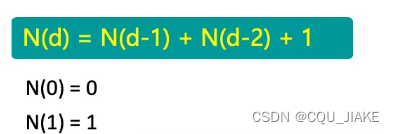BST构建

BST是左孩子都比根节点小，右孩子都比根节点大

二叉搜索树的插入，删除，调整

平衡树理解

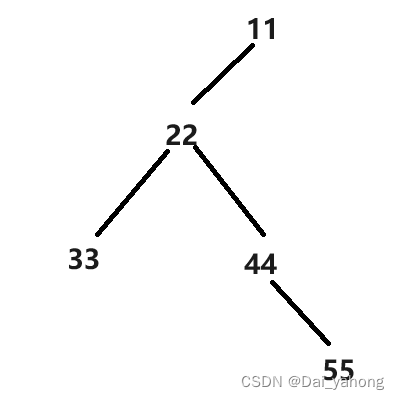
任何一个平衡二叉树，它的中序遍历都是一样的，都是有序的从小到大

之所以有调整，就是谁当根节点不同导致的。

作为根节点，就需要提供两个信息，一个是左孩子，一个是右孩子。

那么中序遍历的过程就是，先由根节点向左一直蔓延，直到到底，然后从左到右依次遍历，遍历到根节点，再从根节点向右遍历蔓延。想象一个有序序列，找到任意一个起点，这个起点就是所谓的树的根节点，那么中序遍历就是左根右，即从左到右，就是从起点（根节点）先一直向左，到底后再逐个输出，那就是中序序列。有这样的性质，就是因为左根右，序列中的每个结点左侧都是它的左孩子，它的右侧都是右孩子或者父母结点

即，左侧只会是左孩子，但右侧可能是右孩子或父母节点，但由于左孩子都小于根节点，所以一旦有右孩子，那么只能先是右孩子，即右孩子的优先级大于父母结点，因为右孩子一定小于父母节点。

AVL树

平衡因子是根节点的定义，即根节点的左右孩子高度差

如这里是4的平衡因子不满足条件，其左子树，右子树高度差大于1

求高度函数

typedef struct node {
    int data;
    node* lchild, * rchild;
}*tree;
int high(tree root) {
    if (root) {
        return max(high(root->lchild), high(root->rchild)) + 1;
    }
    return 0;
}

AVL树的构建

AVL树的调整

中序遍历都是一样的，不一样的就是根节点的确定，即起点的确定

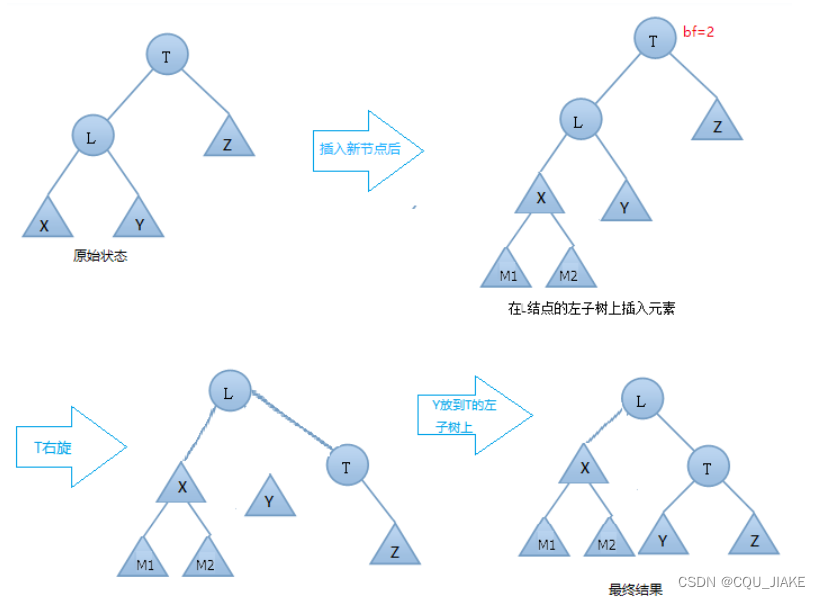
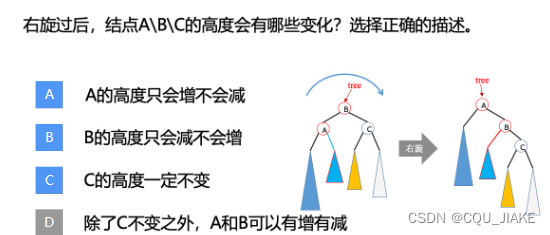
右旋

右旋的具体步骤：

• T向右旋转成为L的右结点
• L的右节点Y 放到 T的左孩子上

如何判断是否为AVL

AVL树高度

由于AVL树的左右子树都是AVL树，

自变量是N,AVL树的高度。那么由于AVL树左右平衡，根节点平衡，所以对于高度为d的AVL树，根节点占一层，那么左子树（默认左子树高一点）高度为d-1,(此时加起来为d)；右子树高度为d-2，因为要满足左右子树高度差不大于1而且结点要尽可能少，所以有

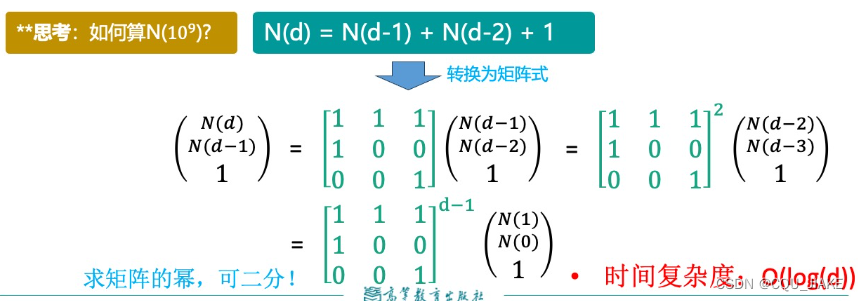
二分求矩阵的幂

快速幂

代码007普通

打赏 收藏 海报 链接