leetcode每日一题35

90. 子集 II

回溯嘛
子集啊排列组合啊棋盘啊都是回溯
 回溯三部曲走起
跟78.子集比，本题给出的数组里存在重复元素了
所以在取元素时，如果同一层里取过某个元素，那么在该层就不能取重复的该元素了
如给出的数组[1,2,2]
可以在某一次递归中第一个取2放进子集，但后面的递归就不允许第一个取2放进子集里了
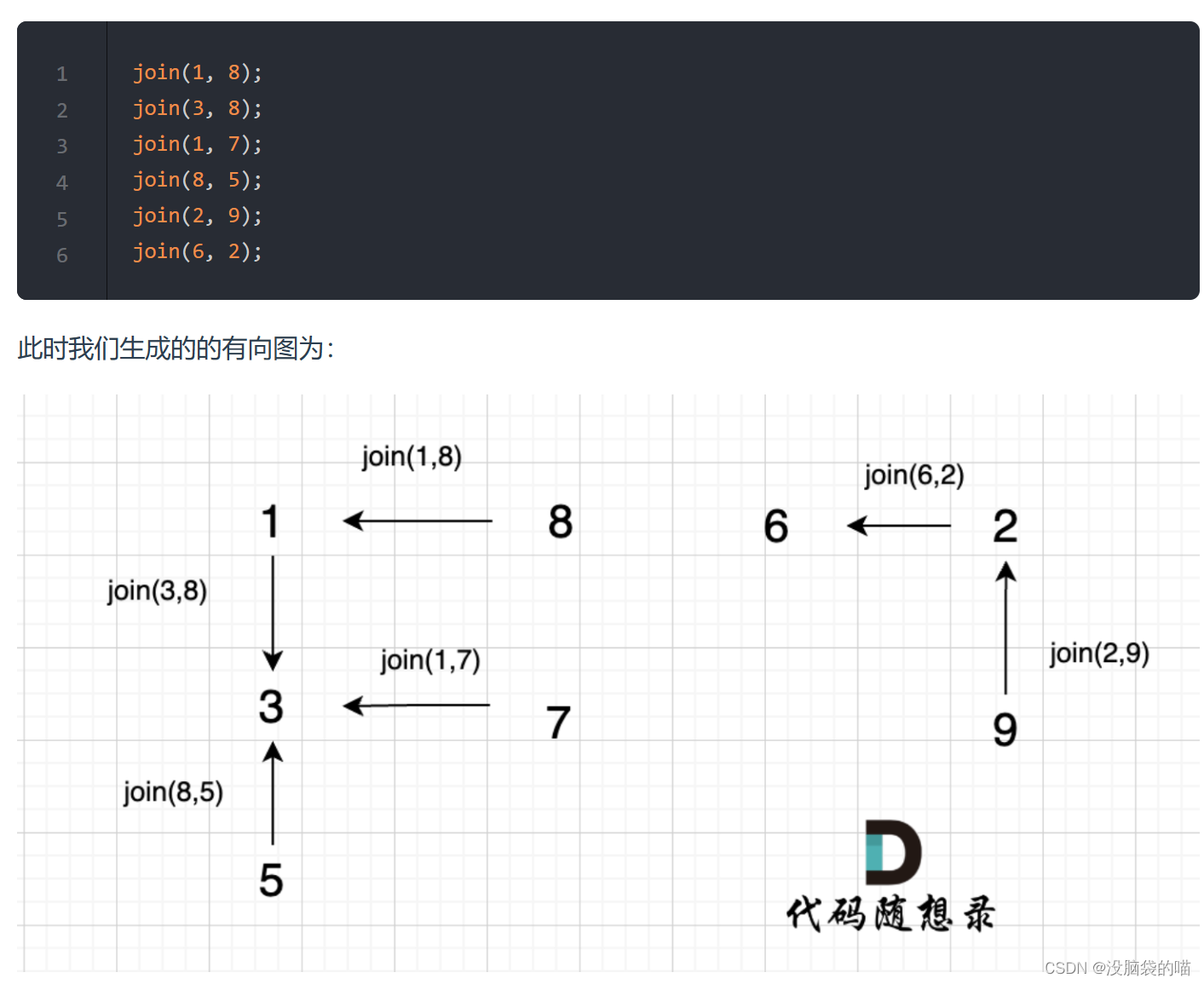
详情可以看代码随想录的图
代码随想录
所以要有一个数组used 记录该层里取过的数

递归函数参数
 回溯问题一般涉及两个全局变量：
保存本次递归中符合条件的结果 path
保存所有符合条件的结果的集合 result
以及回溯函数backtrackin g，因为是求子集问题，所以取过的元素不能重复取，所以回溯时，for循环要从startIndex开始，而不是从0开始

vector<int&gt; path;
vector<vector<int&gt;&gt; result;
void backtracking(vector<int&gt;&amp; nums, int startIndex, vector<bool>&amp; used)

递归终止条件
当此时的startIndex已经大于数组长度时，就没有没取过的数组元素了，本次递归就终止了

if(startIndex>=nums.size()){
	return;
}

单层搜索逻辑
单层的搜索逻辑是
先将取出来的数存入path，再递归调用自身，然后回溯，删掉刚才取出来的数

path.push_back(nums[i]);
backtracking(……);
path.pop_back();

本题中，要判断取的nums[i]有没有使用过
如果没有，那么在bac kt racking要传入used 数组，所以要递归前标记 nums[i]已经被使用过了而递归后，需要回溯，从path中删除 nums[i]，所以要恢复为nums[i]未被使用

if (i > 0 &amp;&amp; nums[i] == nums[i - 1] &amp;&amp; used[i - 1] == false) {
                continue;
}//判定nums[i]有没有使用过
path.push_back(nums[i]);
used[i]=true;
backtracking(nums, i+1,used);
used[i]=false;
path.pop_back();

所以，回溯算法模板为

void backtracking(参数) {
		收集子集result.push_back(path);
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

那么组合起来，本题的回溯函数为

vector<int> path;
vector<vector<int>> result;
void backtracking(vector<int>& nums, int startIndex, vector<bool>& used){
	result.push_back(path);//收集子集
	if(startIndex>=nums.size()){
		return;
	}
	for(int i =startIndex;i<nums.size();i++)
	{
		if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
	                continue;
		}//判定nums[i]有没有使用过
		path.push_back(nums[i]);
		used[i]=true;
		backtracking(nums, i+1,used);
		used[i]=false;
		path.pop_back();
	}
}
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        result.clear();
        path.clear();
        vector<bool> used(nums.size(), false);
        sort(nums.begin(), nums.end()); // 去重需要排序
        backtracking(nums, 0, used);
        return result;
    }

整理一下，得到最终代码：

class Solution {
private:
    vector<int> path;
    vector<vector<int>> result;
    void backtracking(vector<int>& nums, int startIndex, vector<bool>& used){
        result.push_back(path);//收集子集，要放在判定停止条件前，防止漏数
        if(startIndex>=nums.size()){
            return;
        }
        for(int i =startIndex;i<nums.size();i++)
        {
            if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
                        continue;
            }//判定nums[i]有没有使用过
            path.push_back(nums[i]);
            used[i]=true;
            backtracking(nums, i+1,used);
            used[i]=false;
            path.pop_back();
        }
    }
public:
    vector<vector<int>> subsetsWithDup(vector<int>& nums) {
        result.clear();
        path.clear();
        vector<bool> used(nums.size(), false);
        sort(nums.begin(), nums.end()); // 去重需要排序
        backtracking(nums, 0, used);
        return result;
    }
};