本文介绍: 这是因为在计算机系统中,我们是以字节为单位的,每个地址单元都对应着一个字节,一个字节为8 bit 位,但是在C语言中除了8 bit 的 char 之外,还有16 bit (2个字节)的 short 型,32 bit (4个字节)的 long 型(要看具体的编译器),另外,对于位数大于8位的处理器,例如16位或者32位的处理器,由于寄存器宽度大于一个字节,那么必然存在着一个如何将多个字节安排的问题。大端(存储)模式:是指数据的低位字节内容保存在内存的高地址处,而数据的高位字节内容,保存在内存的低地址处。
2.2请简述大端字节序和小端字节序的概念,设计一个小程序来判断当前机器的字节序。(10分)-百度笔试题
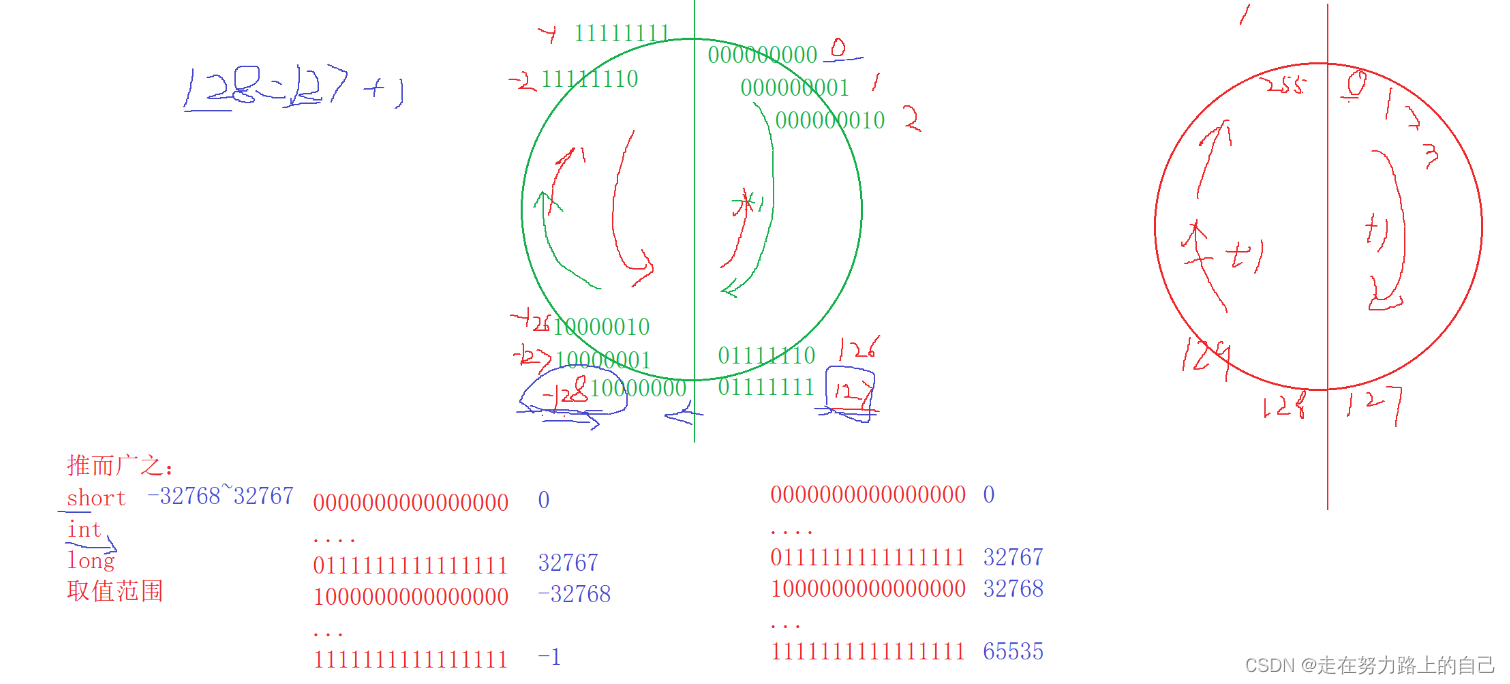
一、整数在内存中的存储
二、大小端字节序和字节序判断
2.1为什么有大小端?
2.2请简述大端字节序和小端字节序的概念,设计一个小程序来判断当前机器的字节序。(10分)-百度笔试题
方法一(char*强制类型转换):
方法二(联合体)
若想了解更多联合体的知识,请见拙作:
2.3unsign打印负数
2.4下列代码打印的结果
2.5下面代码的输出结果
三、浮点数在内存中的存储
3.1 浮点数存的过程
IEEE 754 对有效数字M和指数E,还有一些特别规定。
至于指数E,情况就比较复杂
3.2 浮点数取的过程
指数E从内存中取出还可以再分成三种情况:
E不全为0或不全为1
E全为0
E全为1
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。