最优化理论复习–线性规划性质

上一篇

最优化理论复习–凸集与凸函数

线性规划

图解法
当自变量的个数小于3个时才可以用比较简单的方式求解。

线性规划的性质

1. 可行域是凸集
2. 最优解在极点处取到

由表示定理得可行域中的点可以表示为

x

=

∑

λ

i

x

i

+

∑

μ

j

d

j

x = sum lambda_i x^i + sum mu_j d^j

x=∑λi​xi+∑μj​dj
带入目标函数中得

m

i

n

∑

(

c

x

i

)

λ

i

+

∑

(

c

d

j

)

μ

j

min sum (cx^i) lambda_i + sum (cd^j)mu_j

min∑(cxi)λi​+∑(cdj)μj​

存在最优解的条件是所有

c

d

j

cd^j

cdj非负，不然会无限小下去

最优化问题代数表示

m

i

n

c

x

min cx

min  cx
而

相关定义
这样（2.10）称为一个基本解（

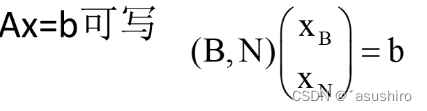
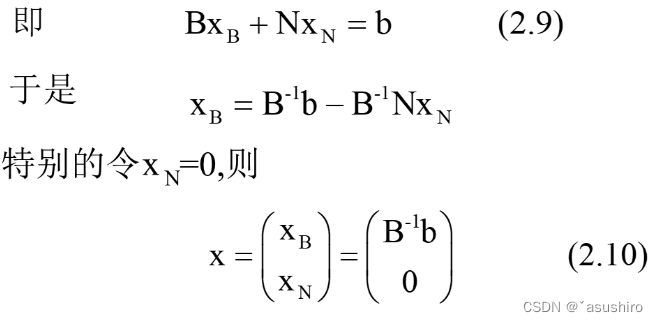
B

−

1

b

B^{-1}b

B−1b），B称为基矩阵(其中B要可逆)，

x

b

x_b

xb​称为基变量
所有基变量的全体称为一组基。

x

N

x_N

xN​为非基变量
如果基变量非零，非基变量为零则称为基本可行解，对应的B称为可行基矩阵
所有

x

B

x_B

xB​称为一组可行基。

如果

x

b

>

0

x_b > 0

xb​>0则称基本可行解,为非退化的，有一个0就是退化的。

基本可行解

⇒

极点

基本可行解 Rightarrow 极点

基本可行解⇒极点
由于这样的B矩阵的数量是有限的，所以解的个数也是有限的，所以能在有限步内求出最优解

下一篇

未完待续

代码007普通

打赏 收藏 海报 链接