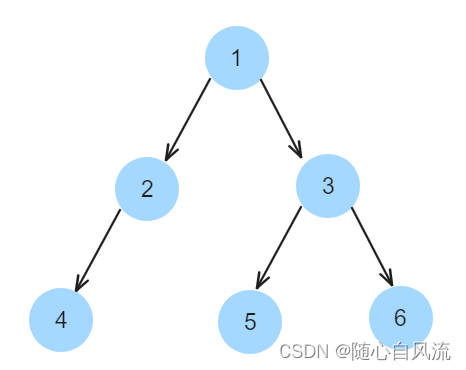
决策树详解
决策树是一种常用的机器学习算法,用于分类和回归任务。它通过一系列规则对数据进行分割,以达到最佳的分类效果。
决策树的核心概念
1. 节点(Node)
- 根节点(Root Node):不包含任何条件的顶层节点,代表整个数据集。
- 内部节点(Internal Node):包含决策条件的节点,用于对数据进行进一步的分割。
- 叶节点(Leaf Node):决策树的末端节点,代表分类或回归的结果。
2. 分割规则(Splitting Rule)
3. 纯度和信息增益
数学原理
1. 信息熵(Entropy)
2. 信息增益
-
I
G
(
S
,
A
)
=
H
(
S
)
−
∑
∈
T
∣
S
∣
∣
S
∣
H
(
S
t
)
IG(S, A) = H(S) – sum_{t in T} frac{|S_t|}{|S|} H(S_t)
IG(S,A)=H(S)−t∈T∑∣S∣∣St∣H(St)
其中
A
A
A 是特征,
T
T
A
A
A 的分割,
S
t
S_t
St 是分割后的子集。
3. 基尼不纯度(Gini Impurity)
应用和实现
- 决策树在构建时,从根节点开始,递归地选择使信息增益最大化(或基尼不纯度最小化)的特征进行分割,直到满足停止条件(如达到预设的深度、节点数据量过少等)。
- 最终得到的树结构可以用于预测新数据的类别或数值。
手写决策树及其数学概念解释
决策树是一种流行的机器学习方法,用于分类和回归任务。它通过创建一系列决策规则来预测数据的类别或值。以下是对决策树中纯度、信息增益、信息熵的概念和计算的解释。
示例数据集
假设我们有一个简单的数据集,包含两个特征(Feature 1和Feature 2)和一个目标类别(Class):
信息熵(Entropy)
H
(
S
)
=
−
∑
i
=
1
c
p
i
2
p
i
H(S) = –sum_{i=1}^{c} p_i log_2 p_i
H(S)=−i=1∑cpilog2pi
其中,
S
S
S 是数据集,
c
c
c 是类别的数量,
p
i
p_i
pi 是类别
i
i
i 在数据集中的比例。
初始信息熵
对于上述数据集,两个类别各占一半,所以信息熵为:
H
(
S
)
=
−
(
0.5
log
2
0.5
+
0.5
log
2
0.5
)
=
1
H(S) = –left(0.5 log_2 0.5 + 0.5 log_2 0.5right) = 1
H(S)=−(0.5log20.5+0.5log20.5)=1
信息增益(Information Gain)
信息增益是选择分割规则的依据,基于信息熵的减少量计算。信息增益定义为:
I
G
(
S
,
A
)
=
H
(
S
)
−
∑
t
∈
T
∣
S
t
∣
∣
S
∣
H
(
S
t
)
IG(S, A) = H(S) – sum_{t in T} frac{|S_t|}{|S|} H(S_t)
IG(S,A)=H(S)−t∈T∑∣S∣∣St∣H(St)
其中
A
A
A 是特征,
T
T
T 是基于特征
A
A
A 的分割,
S
t
S_t
St 是分割后的子集。
分割示例
-
信息增益为:
I
G
(
S
,
Feature 1
)
=
1
−
(
2
4
×
0
+
2
4
×
0
)
=
1
IG(S, text{Feature 1}) = 1 – left(frac{2}{4} times 0 + frac{2}{4} times 0right) = 1
IG(S,Feature 1)=1−(42×0+42×0)=1
决策树构建
- 开始:从根节点开始,包含所有数据。
- 分割选择:选择使信息增益最大化的特征进行分割。
- 创建分支:为每个唯一值创建一个分支。
- 递归:对每个分支重复上述过程。
- 停止条件:当达到某个条件(如纯度达到一定程度,达到最大深度等)时停止。
信息增益(Information Gain)详解
信息增益是决策树算法中用于选择特征分割点的关键指标,它基于信息熵的减少量来评估特征的重要性。
信息熵(Entropy)
信息熵是一种衡量数据集不确定性的度量。在决策树中,它用来评估数据集中的混乱程度。信息熵定义为:
H
(
S
)
=
−
∑
i
=
1
c
p
i
log
2
p
i
H(S) = –sum_{i=1}^{c} p_i log_2 p_i
H(S)=−i=1∑cpilog2pi
其中,
S
S
S 是数据集,
c
c
c 是类别的数量,
p
i
p_i
pi 是类别
i
i
i 在数据集中的比例。
示例:计算信息熵
假设我们有一个数据集,其中有9个样本属于类别A,5个样本属于类别B。信息熵计算如下:
H
(
S
)
=
−
(
9
14
log
2
9
14
+
5
14
log
2
5
14
)
≈
0.940
H(S) = -left(frac{9}{14} log_2 frac{9}{14} + frac{5}{14} log_2 frac{5}{14}right) approx 0.940
H(S)=−(149log2149+145log2145)≈0.940
信息增益(Information Gain)
信息增益衡量了在某个特征上进行分割后信息熵的减少。信息增益越高,意味着该特征对于分类的贡献越大。信息增益定义为:
I
G
(
S
,
A
)
=
H
(
S
)
−
∑
t
∈
T
∣
S
t
∣
∣
S
∣
H
(
S
t
)
IG(S, A) = H(S) – sum_{t in T} frac{|S_t|}{|S|} H(S_t)
IG(S,A)=H(S)−t∈T∑∣S∣∣St∣H(St)
其中
A
A
A 是特征,
T
T
T 是基于特征
A
A
A 的分割,
S
t
S_t
St 是分割后的子集。
示例:计算信息增益
假设我们根据某个特征(例如Feature 1)将上述数据集分为两个子集:
首先计算子集的信息熵:
H
(
S
1
)
=
−
(
6
8
log
2
6
8
+
2
8
log
2
2
8
)
≈
0.811
H(S_1) = -left(frac{6}{8} log_2 frac{6}{8} + frac{2}{8} log_2 frac{2}{8}right) approx 0.811
H(S1)=−(86log286+82log282)≈0.811
H
(
S
2
)
=
−
(
3
6
log
2
3
6
+
3
6
log
2
3
6
)
=
1
H(S_2) = -left(frac{3}{6} log_2 frac{3}{6} + frac{3}{6} log_2 frac{3}{6}right) = 1
H(S2)=−(63log263+63log263)=1
I
G
(
S
,
Feature 1
)
=
0.940
−
(
8
14
×
0.811
+
6
14
×
1
)
≈
0.048
IG(S, text{Feature 1}) = 0.940 – left(frac{8}{14} times 0.811 + frac{6}{14} times 1right) approx 0.048
IG(S,Feature 1)=0.940−(148×0.811+146×1)≈0.048
结论
信息增益帮助我们确定哪个特征在分割数据时更有效。在构建决策树时,我们通常选择具有最高信息增益的特征作为分割点,以此逐步构建树的结构,从而提高分类的准确性。
原文地址:https://blog.csdn.net/h52013141/article/details/134757553
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_45388.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!