本文介绍: 输入是给定一个图或者超图,记作G=(V,E,W),V表示点集,E表示边集,W表示每条边的权重。由于L拉普拉斯算子是一个半正定的矩阵,那么它可以被表示,其中是由特征值组成的对角矩阵。对应每个顶点,可能存在一个向量x,这个x是原始信号,那么就是原始信号在谱域的表达,如果想把谱域中的信号在变回去,只要与U相乘就可以了。基于以上,对于卷积的定义就能表示为把原始信号x和作为卷积核的信号y投影到谱域中做点积,然后在重新回来,这里利用卷积定理。然后再到这个式子,是因为gθ不再是自由参数了,而是受。
首先是卷积的谱方法。
输入是给定一个图或者超图,记作G=(V,E,W),V表示点集,E表示边集,W表示每条边的权重。
由于L拉普拉斯算子是一个半正定的矩阵,那么它可以被表示,其中
,
是由特征值组成的对角矩阵。
对应每个顶点,可能存在一个向量x,这个x是原始信号,那么就是原始信号在谱域的表达,如果想把谱域中的信号
在变回去,只要与U相乘就可以了。
基于以上,对于卷积的定义就能表示为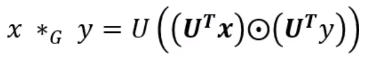 把原始信号x和作为卷积核的信号y投影到谱域中做点积,然后在重新回来,这里利用卷积定理。
把原始信号x和作为卷积核的信号y投影到谱域中做点积,然后在重新回来,这里利用卷积定理。
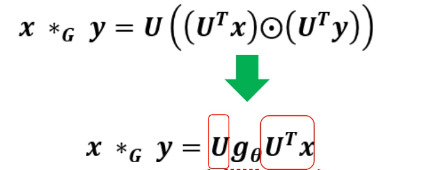
这个公式是怎么来的呢,主要是卷积核并不是在原始空间中,而是在谱域里面了,那么就不需要投影了,整个谱卷积就分三步:
空间方法
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。

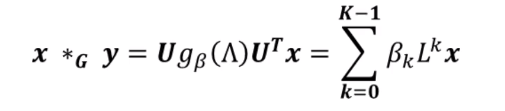
 谱
谱





