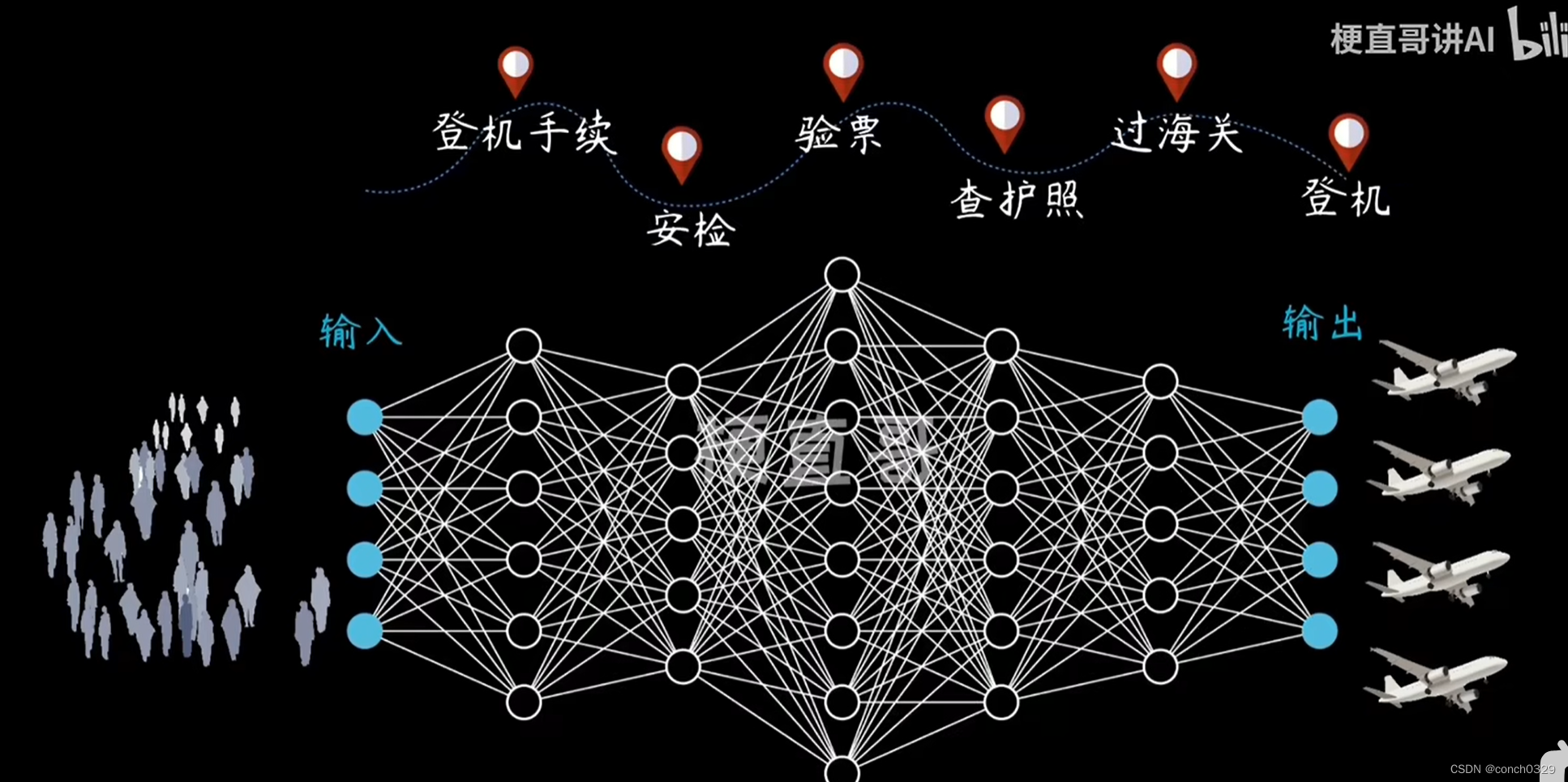
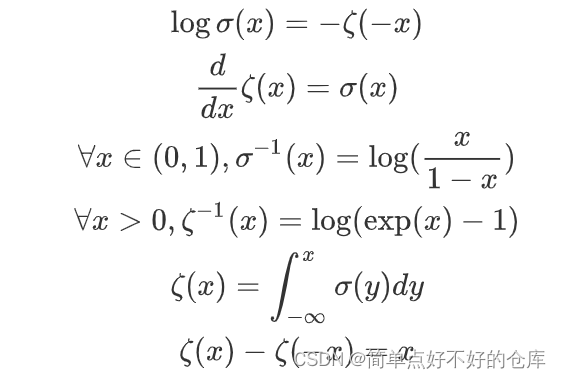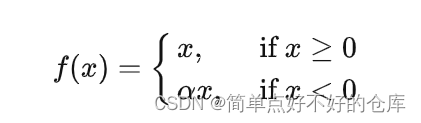本文介绍: sigmoid函数可以将输入映射到0-1之间,常用于机器学习和深度学习中的激活函数。因此,logistic函数可以用于将输入映射到0或1之间。常用的激活函数,其实也是特殊的logistic函数。特殊点记忆: 经过 [0 , 1]定义域:【负无穷,正无穷】
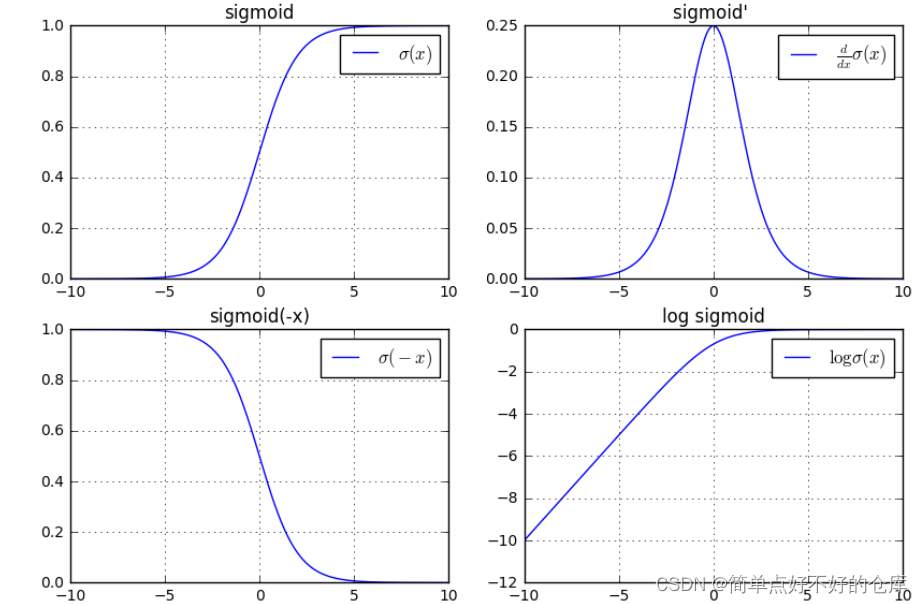
Sigmoid

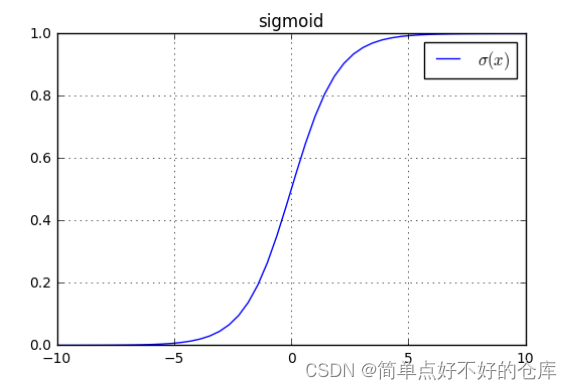
值域: 【0,1】
定义域:【负无穷,正无穷】
特殊点记忆: 经过 [0 , 0.5]
关键点[0,0.5]处的导数是 0.025
相关导数:
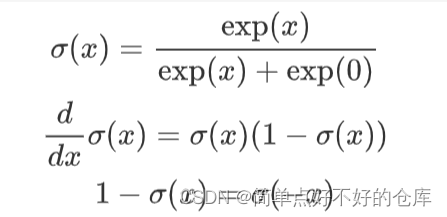
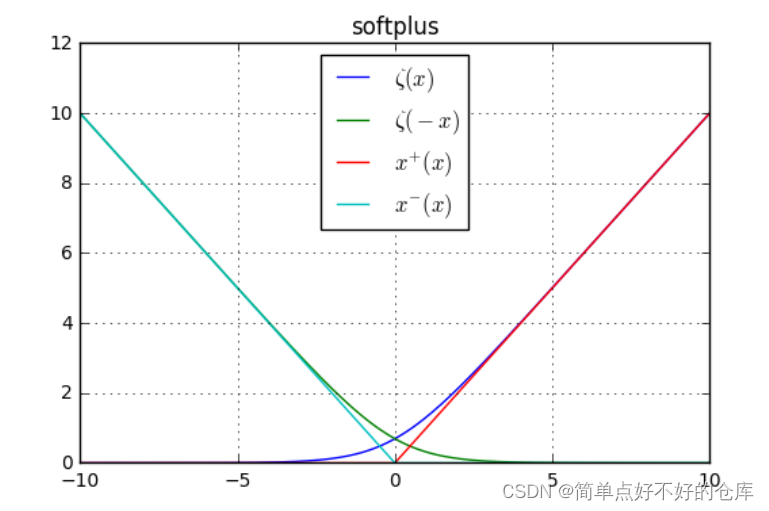
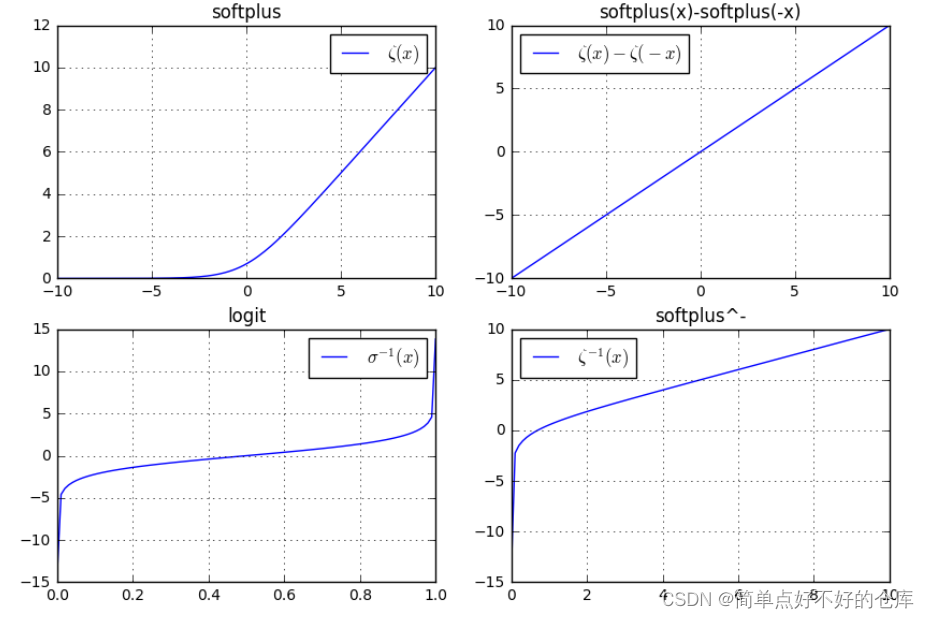
softplus函数

tanh
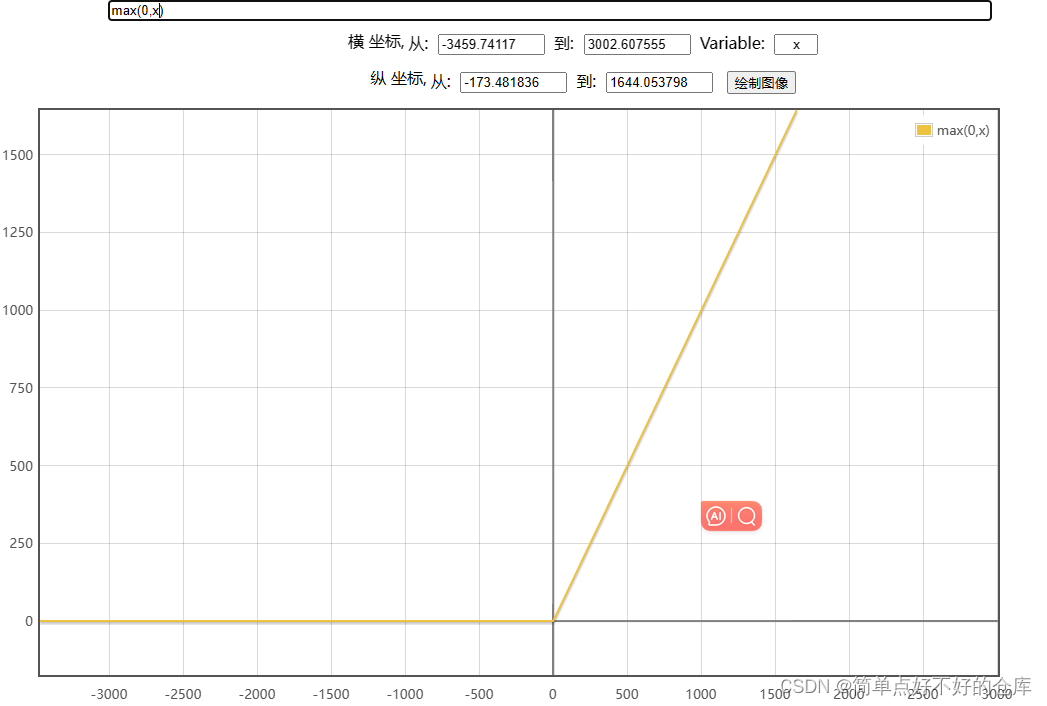
ReLu(x)
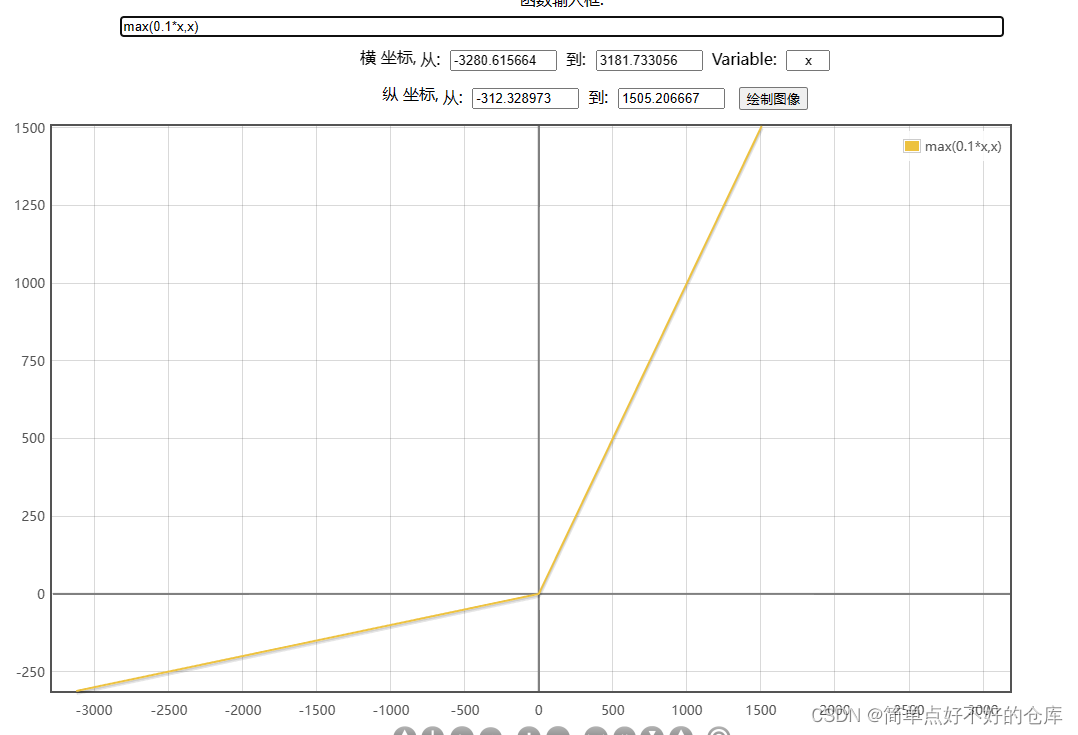
Leaky-Relu
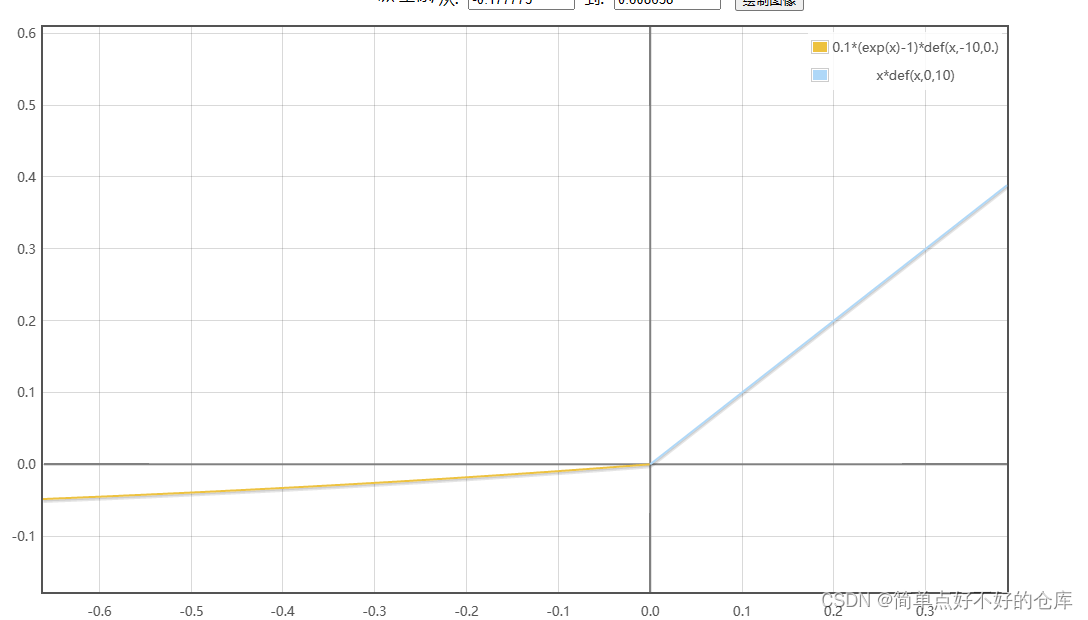
ELU
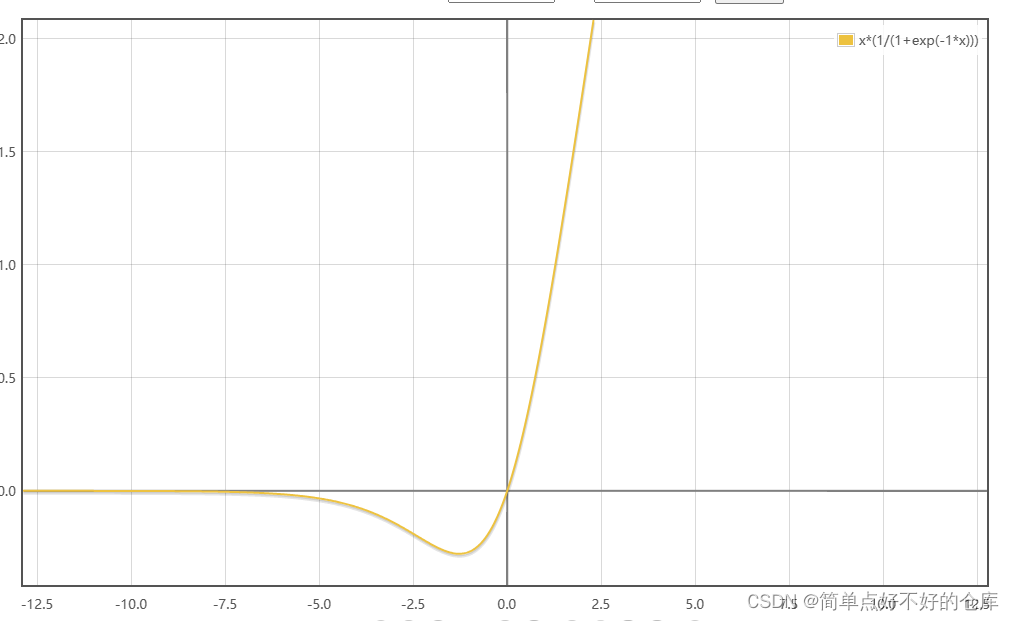
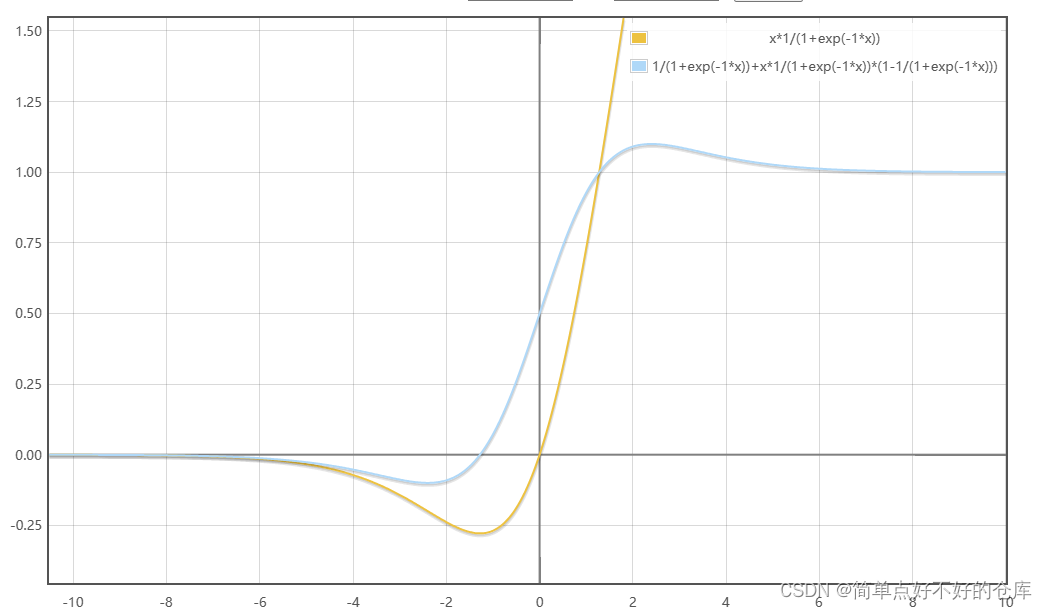
SiLu/ Swish
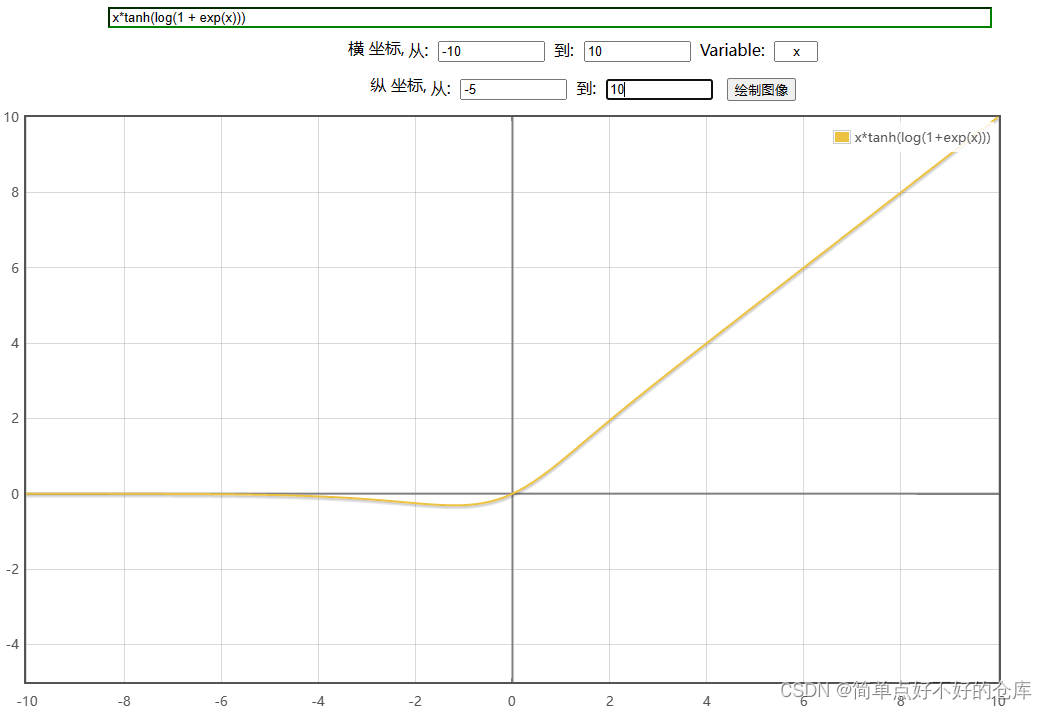
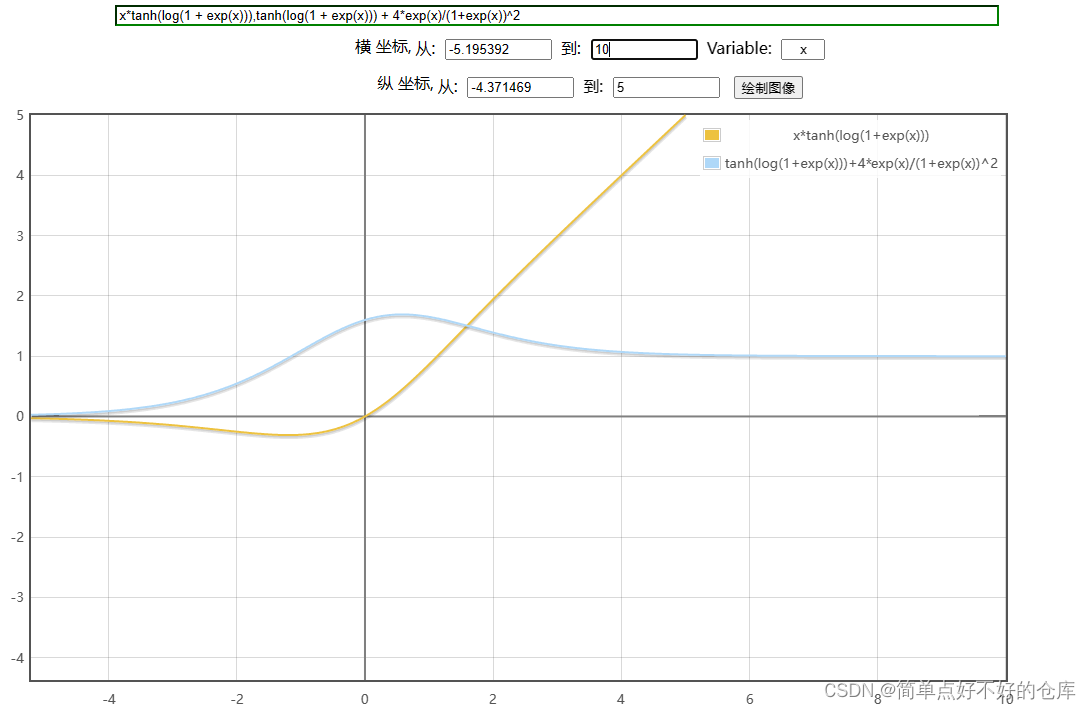
Mish
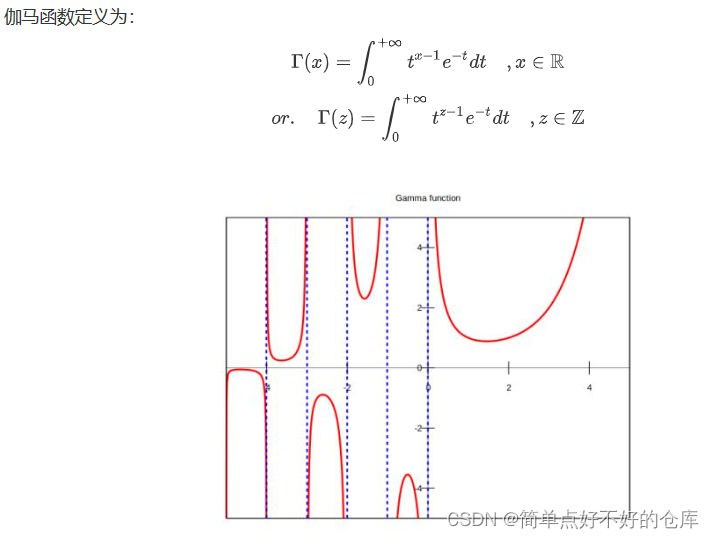
伽玛函数
beta函数
Ref
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。