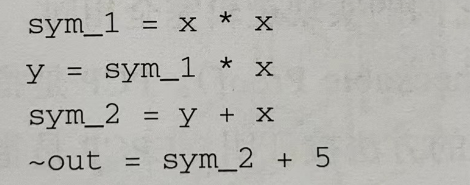我的隐私计算学习——零知识证明

本文介绍: 安全保护技术（五）

此篇是我笔记目录里的安全保护技术（五），前篇可见：

隐私计算安全保护技术（一）：我的隐私计算学习——混淆电路

隐私计算安全保护技术（二）：我的隐私计算学习——秘密共享

隐私计算安全保护技术（三）：我的隐私计算学习——门限签名

隐私计算安全保护技术（四）：我的隐私计算学习——同态加密

笔记内容来自多本书籍、学术资料、白皮书及ChatGPT等工具，经由自己阅读后整理而成。

（五）零知识 证明

笔记分享 | 一文了解零知识证明基础知识

零知识证明（Zer o-Knowledge Pro o f，ZKP）技术，指的是证明者能够在不向验证者提供任何有用信息的情况下，使验证者相信某个论断是正确的，允许证明者（Pr over）、验证者（Ver i f ie r）证明某项提议的真实，却不必泄露除了“提议是真实的”之外的任何信息，这项技术经常用于区块链应用。网上有很多关于零知识证明的例子辅助理解。

零知识证明一般可分为交互式零知识证明和非交互式零知识证明。交互式零知识证明存在种种缺点，如要求证明者时刻在线并等待挑战；验证者如需验证，需要与证明者进行多次交互。更复杂的是，如果这个时候还有其他人想要参与，那么如何向其他人证明？显然，交互式零知识证明应用场景存在一定的限制。于是非交互式零知识证明（Non-In t er active Zer o Knowledge，NIZK）闪亮登场，其中 zkSNARK 技术最为典型，它的命名几乎包含其所有技术特征：

Suc cin ct：最终生成的证明具有简洁性，也就是说最终生成的证明足够小，并且与计算量大小无关。
Non–int er active：没有或者只有很少的交互。对于 zkSNARK 来说，证明者向验证者发送一条信息之后几乎没有交互。此外，zkSNARK还常常拥有“公共验证者”的属性，意思是在没有再次交互的情况下任何人都可以验证。这种属性对于区块链来说是至关重要的。
Argum e n ts：证明者在不知道 Wi tnes s（私密的数据，只有证明者知道）的情况下，构造出证明是不可能的（这样的证明系统叫作一个 Argument）。
zero–knowledge：验证者无法获取证明者的任何隐私信息。

zkSNARK 的原理极其复杂，这里只是简单介绍一下其工作流程：

（1）将所要声明的内容的计算算法用算术电路来表示（所有的NP问题都可以有效地转换为算术电路）。

（2）将电路用 R1CS （Rank-1 Con s train t Sy stem，一阶约束系统）描述。

（3）将 R1CS 变换成 QAP（Qua dr a t ic Ari t hm e ti c Problem）形式。R1CS 与 QAP 形式上的区别是 QAP 使用多项式来代替点积运算，而它们的实现逻辑完全相同。

（4）QAP 还要变换成 LPCP （Lin e ar Prob a bi list i call y Che ck a ble Proof）。PCP 是指所有的 NP 问题都可以在多项式时间内通过概率验证的方法被证明。LPCP 是指任意一个多项式都可以通过随机验证多项式在几个点上取值来确定多项式的每一项系数是否满足特定的要求。

（5）还要通过一系列步骤将 LPCP 变换成 LIP (Lin e ar Int er active Proof)，再转变成 LNIP (Linear Non-Int er active Proof)，最后才能构建出一个 zkSNARK。

————————（2）中提到的 R1CS 是什么？—————————

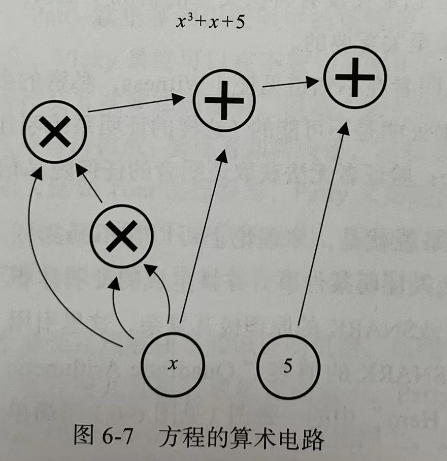
描述电路的语言很多，如 R1CS、QAP、Tin yRAM、b a cs 等，目前主流的零知识证明的开发框架仍然使用 R1CS 来描述电路。这里举一个例子来说明 R1CS 是如何描述电路的。假设 Pa tty 希望证明自己知道如下方程的解：x³+x+5=~out，其中 ~out 是大家都知道的一个数，这里假设 ~out 为 35，而 x=3 就是方程的解。该方程的算术电路如图所示。

———————— R1CS 之后的步骤？—————————

拍平

首先需要将算术电路拍平（Flattenin g）成多个 x=y 或者 x=y(op)z 形式的等式，上述算术电路可以转化成如下几个等式：

转化成三向量组

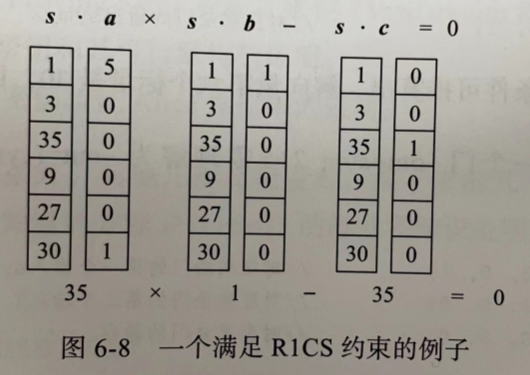
R1CS 是一个由三个向量(a,b,c)组成的序列，还有一个解向量 s，s 必须满足 s·a×s·b-s·c=0 这个约束，这里的解向量 s 就是见证（Witness）。

然后要将每个逻辑门（即“拍平”后的每一个声明语句）转化成一个三向量组(a, b, c)，转化的方法取决于声明是什么运算（+、-、×、/）和声明的参数是变量还是数字。在这个例子中，除了“拍平”后的 5 个变量（‘x’、‘~out’、 ‘sym_1’、‘y’、 ‘sym_2’）外，==还需要在第一个分量位置引人一个冗余变量 ~one 来表示数字 1。就这个系统而言，一个向量所对应的 6 个分量是:（‘~one’、‘x’、‘~out’、‘sym_1’、 ‘y’、 ‘sym_2’)。变量和分量也可以是其他顺序，只要对应起来即可。

Patty要计算解向量 s。可以看出，如果解向量 s 的第二个标量是3，第四个标量是9，无论其他标量是多少，都满足 s·a×s·b-s·c=0 这个约束。第一个分量位置默认使用1，因此解向量 s=[1,3,?,9,?,?]。

类似地，第二个乘法门 y=sym_1×x 的三向量组(a, b, c)为：

将向量组代入约束条件可推算出，解向量第五个标量是27，即 s= [1,3,?,9,27,?]。

第三个加法门 sym_2=y+x 略有不同，需理解为 sym_2=(y+x)×1 的三向量组(a,b,c)为：

将向量组代入约束条件可推算出，解向量第六个标量是30，即 s=[1,3,?,9,27,30]。

类似地，最后一个门 ~out=sym_2+5 需理解为 ~out=(sym_2+5)×1 的三向量组(a,b,c)为：

将向量组代入约束条件可推算出，解向量第三个标量是35,即 s=[1,3,35,9,27,30]。

获得完整的R1CS

汇总上面所得的向量组就可以得到完整的 R1CS：

得到完整的 R1CS 后，还要将其转化为 QAP 形式，这部分属于零知识证明开发框架的底层实现。应用 zkSNARK 技术实现一个非交互式零知识证明应用的开发步骤大致如下：

（1）使用 R1CS 形式编写计算的验证逻辑；

（2）生成证明密钥（Prov in g Key）和验证密钥(Veri fi cat ion Key)；

（3）Patty 使用证明密钥和其可行解构造证明；

（4）Vi cky 使用验证密钥验证 Ali ce 发过来的证明。

接下来介绍使用 lib sn ar k 框架实现 Patty 知道的方程 x³+x+5=35 的解的零知识证明。

开源框架 li bsnar k

li bsnark 是用于开发 zkSNARK 应用的C++代码库，相关代码在 GitHub 上开源：[ GitHub – scipr-lab/libsnark: C++ library for zkSNARKs ]。libsnark 框架提供了多个通用证明系统的实现，其中使用较多的是 Groth16。Groth16 计算分为以下 3 个部分：

Setup：针对电路生成证明密钥和验证密钥。

Prove：在给定见证（Witness）和声明（Statement）的情况下生成证明。

Verify：通过验证密钥验证证明是否正确。

libsnark 框架中有一个很重要的概念，原型板protoboard，用来快速搭建算术电路，把所有变量、组件和约束串联起来。还有另外两个概念，public input 和 private witness，它们分别对应框架里的 primary 和 auxiliary 变量。那么如何区分这些变量呢？这里需要借助 protoboard 的 set_input_sizes(n) 函数来声明与其连接的 public、primary 变量的个数 n。
out.allocate(pb, "out");
x.allocate(pb, "x");
sym_1.allocate(pb, "sym_1");
y.allocate(pb, "y");
sym_2.allocate(pb, "sym_2");
// 表明与pb连接的前1个变量(out)是公有的，其余都是私有的。
pb.set_input_sizes(1);
所有变量相连后还需要确定的是这些变量之间的约束关系，add_r1cs_constrain 函数。
// Add R1CS constraints to protoboard 添加约束
// x*x = sym_1
pb.add_r1cs_constraint(r1cs_constraint<FieldT&gt;(x, x, sym_1));
// sym_1 * x = y
pb.add_r1cs_constraint(r1cs_constraint<FieldT&gt;(sym_1, x, y));
// y + x = sym_2
pb.add_r1cs_constraint(r1cs_constraint<FieldT&gt;(y + x, 1, sym_2));
// sym_2 + 5 = ~out
pb.add_r1cs_constraint(r1cs_constraint<FieldT&gt;(sym_2 + 5, 1, out));
电路构建完毕，约束添加完成之后就可以生成密钥了。
// 使用生成算法生成公共参数（证明密钥和验证密钥），即trust setup,证明密钥和验证密钥分别通过keypair.pk和keypair.vk获得
const r1cs_constraint_system<FieldT&gt; constraint_system = pb.get_constraint_system();
const r1cs_ppzksnark_keypair<default_r1cs_ppzksnark_pp> keypair = r1cs_ppzksnark_generator<default_r1cs_ppzksnark_pp>(constraint_system);
// 证明者需要生成证明，为public input和witness提供具体数值。
pb.val(x) = 3;
pb.val(out) = 35;
pb.val(sym_1) = 9;
pb.val(y) = 27;
pb.val(sym_2) = 30;
生成证明之后要把 public input 以及 witness 的数值传给 r1cs_pp zk snark_pr over 函数，以生成证明，并分别通过 pb.primary_input 和 pb.auxiliary_input 访问获得 public input 以及 witness。生成的证明用 proof 变量保存。
const r1cs_ppzksnark_proof<default_r1cs_ppzksnark_pp> proof = r1cs_ppzksnark_prover<default_r1cs_ppzksnark_pp>(keypair.pk, pb.primary_input(), pb.auxiliary_input());
最后，验证者使用 r1cs_ppzksnark_verifier_str ong_IC 函数校验证明，如果verified为True，则证明验证成功。
bool verified = r1cs_ppzksnark_verifier_strong_IC<default_r1cs_ppzksnark_pp>(keypair.vk, pb.primary_input(), proof);
———————— 可复用的电路 Gad get ？—————————

上述步骤就是构造零知识证明的过程，可以看到，需要自己构造算术电路，添加约束，生成密钥等。如果能将一些常用的算术电路预制到库中，将会给编程带来很大的方便。libsnark 框架中的 gad get lib1 和 gad get lib2 就提供了这样的现成库。在原型板中使用 Gad get 非常简单，这里以一个用来比较大小的 Gad get 为例进行演示：

在实际应用中，零知识证明的 trusted setup、prove、verify 三个阶段会由不同的角色分别开展，注意，每个阶段都需要构造原型板。最终实现的效果就是证明者（Prover）给验证者（Verifier）一段简短的 proof 和 public input，验证者可以自行校验某命题是否成立。还有一种特殊的零知识证明场景是，交易过程的交易金额也属于隐私信息，希望能得到保护。也就是说，要在参与方不知道交易金额的情况下验证这笔交易是否收支平衡。这就需要用到另外一种技术——同态承诺（Homomorphic Commitment）。要了解同态承诺，首先了解什么是密码学的“承诺”。

承诺，指的是对一个既定的确定性的事实（隐私数据）进行陈述，保证未来的某个时间验证方可以验证承诺的真假。承诺一般包含承诺方和验证方两个角色，通常分为 3 个阶段：

初始化阶段：承诺方根据算法选择相应的参数进行初始化，并根据算法公开相关参数。
生成阶段：承诺方选择一个暂不公开的敏感数据 v，计算出对应的承诺 C 并公开。
披露阶段：也称为承诺打开-验证（Open-Verify）阶段，承诺方公布隐私数据 v 的明文和其他必要参数，验证方重复承诺 C 生成的计算过程，比较新生成的承诺与之前接收到的承诺 C 是否一致，一致则表示验证成功，否则失败。

承诺具备以下两个特性：

隐匿性：做出的承诺是密文形式，在打开承诺之前，验证方无法知晓承诺方的隐私数据内容。
绑定性：一旦承诺生成并公开，承诺方不能将已承诺的隐私数据换成（或解释成）另一个不同的数据。

———————— 哈希承诺？—————————

基于以上特性，很容易就想到，我们可以通过哈希算法生成哈希承诺。哈希承诺适用于对隐私数据机密性要求不高的应用场景，而对于机密性要求高的场景，哈希承诺因其不具备随机性，提供的安全性比较有限。因为对于同一个敏感数据 v，H(v) 的值总是固定的，这就有被暴力穷举攻破的风险了。另外，哈希承诺不具备同态特性，多个相关的承诺值之间无法进行密文运算和交叉验证，对于构造复杂密码学协议和多方安全计算方案的作用比较有限。

———————— Pede rsen 同态承诺？—————————

首先简单说明一下理解同态承诺如何工作所必须了解的 ECC 属性（Ell ip tic Curve Cryptography，椭圆曲线密码学，ECC）。

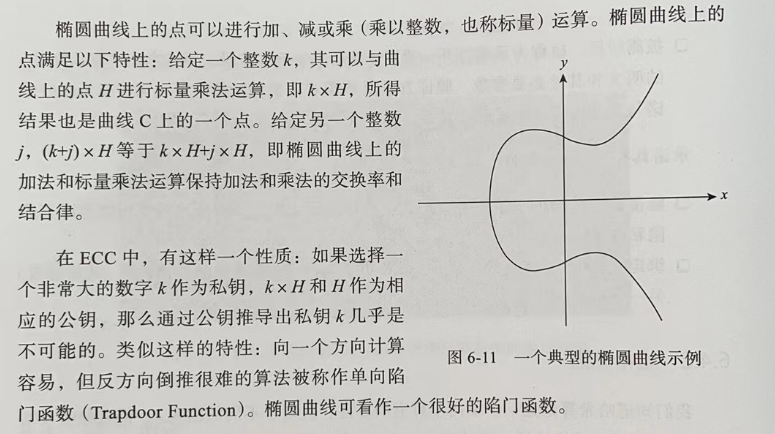
Pederson 同态承诺（简称 Pede rsen 承诺）是由 Torben Pry ds Pedersen 于1992年在“Non-Interac tive and Informat ion-Theore tic Secure Verifiable Sec ret Sharing”一文中提出的一种承诺。目前，Pedersen 承诺主要搭配椭圆曲线密码学使用，具有基于离散对数困难问题的强绑定性以及同态加法特性。Pederson 同态承诺的核心公式表达为：

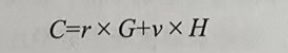
上述公式中，C 为生成的承诺值，G、H 为特定椭圆曲线上的生成点，r 代表盲因子（Blinding Factor），v 则代表着隐私信息。由于 G、H 为特定椭圆曲线上的生成点，所以 r×G、v×H 可以看作相应曲线上的公钥（r、v可以视为私钥）。Pedersen 承诺还具备加法同态特性，这是椭圆曲线点运算的性质决定的。假设有两个要承诺的信息 v₁、v₂，随机数 r₁、r₂，生成对应的两个承诺为:

则有如下特性：

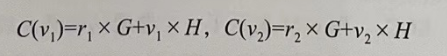
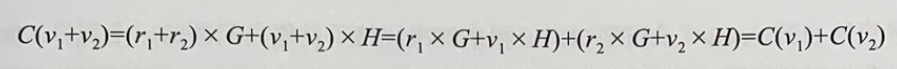
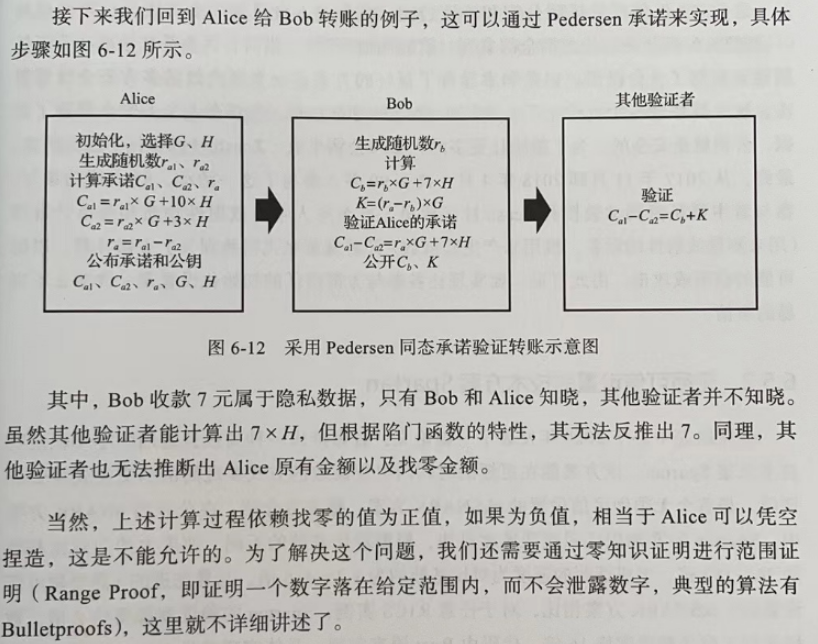
接下来理解一个例子，基于 Pederson 同态承诺的转账：

扩展——Spartan

微软研究中心于2020年发表了一篇论文，宣布推出一种高效且通用的零知识证明技术方案 Spartan。该方案能在更短的时间内以更高效的方式实现简洁非交互式零知识证明，是首个无须做可信设置的zkSNARK方案。据官方介绍，在公开的 SNARK 方案中，Spartan 的零知识证明验证速度最快，根据对比基数的不同，速度大约为对比基数的36~152倍，生成证明的速度为对比基数的为1.2~416倍。与最先进的（需要做可信设置的）zkSNARK方案相比，对于任意 RICS 实例，Spartan 的验证器都要快2倍，数据并行工作负载速度快16倍。代码由 Rust 语言实现，具体实现参见[ https://github.com/microsoft/Spartan ]。

总结：

上面提到的 zkSNARK 算法必须能够实现各参与方都信任的初始化设置，因为零知识证明 zkSNARK 算法依赖于可信的公共参数，即在算法的初始化阶段，需要一些原始随机数来生成 zkSNARK 的证明公钥和验证公钥。如果原始随机数被泄露，拥有原始随机数的人可以随意伪造证明，摧毁整个系统的正确性。总而言之，非交互式零知识证明颇受欢迎，但其生成和验证任何 zkSNARK 证明都需要事先生成一个公共参考字符串（CRS），这是它一个不可忽视的缺点。任何了解如何生成 CRS 的人都可以伪造证明，因此可靠性低。目前，在 trusted setup 设置阶段中使用多方安全技术是比较主流的方案，而无须可信设置的技术方案更是值得关注。