Python高级数据结构——树（Tree）

Python中的树（Tree）：高级数据结构解析

树是一种非常重要且常用的数据结构，它的层次结构使得在其中存储和检索数据变得高效。在本文中，我们将深入讲解Python中的树，包括树的基本概念、表示方法、常见类型、遍历算法以及实际应用。我们将通过代码示例演示树的操作和应用。

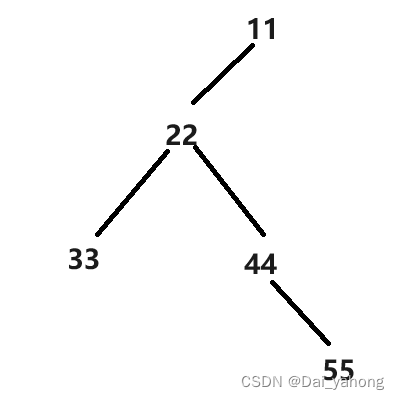
基本概念

树是由节点和边组成的层次结构。树的基本概念包括：

1. 节点（Node）： 树中的基本元素，包含一个数据元素以及指向它的子节点的引用。
2. 根节点（Root）： 树的顶端节点，是整个树的起始点。
3. 叶子节点（Leaf）： 没有子节点的节点，位于树的末端。
4. 父节点（Parent）： 有子节点的节点。
5. 子节点（Child）： 由父节点指向的节点。
6. 深度（Depth）： 节点所在的层数，根节点深度为0。
7. 高度（Height）： 树的最大深度。
   根据节点的子节点数量，树可以分为二叉树、三叉树等。

树的表示方法

在Python中，树可以使用多种方式表示，其中两种常见的表示方法是节点类和字典。

节点类表示

使用类表示树的节点，每个节点包含数据、左子节点和右子节点。

class TreeNode:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

# 示例
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)

字典表示

使用字典表示树的层次结构，每个节点的键是节点的数据，值是其子节点的字典。

tree_dict = {
    1: {
        2: {
            4: {},
            5: {},
        },
        3: {},
    }
}

常见类型的树

二叉树

二叉树是每个节点最多有两个子节点的树，包括二叉搜索树、平衡二叉树等。

class BinaryTreeNode:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

二叉搜索树

二叉搜索树（Binary Search Tree，BST）是一种有序的二叉树，对于每个节点，其左子树的所有节点值都小于该节点值，右子树的所有节点值都大于该节点值。

class BSTNode:
    def __init__(self, key):
        self.key = key
        self.left = None
        self.right = None

# 示例
root = BSTNode(8)
root.left = BSTNode(3)
root.right = BSTNode(10)
root.left.left = BSTNode(1)
root.left.right = BSTNode(6)

平衡二叉树

平衡二叉树是一种特殊的二叉搜索树，其左右子树的高度差不超过1。

字典树（Trie）

字典树是一种多叉树结构，用于存储动态集合或关联数组，通常用于字符串的检索。

class TrieNode:
    def __init__(self):
        self.children = {}
        self.is_end_of_word = False

# 示例
root = TrieNode()
root.children['a'] = TrieNode()
root.children['b'] = TrieNode()
root.children['a'].children['n'] = TrieNode()
root.children['a'].children['n'].is_end_of_word = True

树的遍历算法

树的遍历是按照一定规则依次访问树的所有节点，主要有前序遍历、中序遍历和后序遍历。

前序遍历

前序遍历按照根节点、左子树、右子树的顺序进行遍历。

def pre_order_traversal(node):
    if node:
        print(node.data, end=" ")
        pre_order_traversal(node.left)
        pre_order_traversal(node.right)

# 示例
pre_order_traversal(root)

中序遍历

中序遍历按照左子树、根节点、右子树的顺序进行遍历。

def in_order_traversal(node):
    if node:
        in_order_traversal(node.left)
        print(node.data, end=" ")
        in_order_traversal(node.right)

# 示例
in_order_traversal(root)

后序遍历

后序遍历按照左子树、右子树、根节点的顺序进行遍历。

def post_order_traversal(node):
    if node:
        post_order_traversal(node.left)
        post_order_traversal(node.right)
        print(node.data, end=" ")

# 示例
post_order_traversal(root)

实际应用

树的应用非常广泛，其中一些常见的应用包括：

1. 文件系统： 文件和目录的层次结构可以表示为树。
2. 数据库索引： 数据库中的索引结构通常采用B树或B+树。
3. 表达式树： 将数学表达式表示为树结构，方便计算和优化。
4. 解析树： 用于解析语法结构，如编译器中的语法树。
   通过理解树的基本概念、表示方法、常见类型和遍历算法，您将能够更好地应用树结构在实际问题中。在Python中，使用节点类或字典来表示树的结构，同时使用递归实现树的遍历算法，是处理树结构的常用方式。

我的博客即将同步至腾讯云开发者社区，邀请大家一同入驻：链接

代码007普通

打赏 收藏 海报 链接