群同态
ρ
:
G
1
(
,
⋅
)
→
G
2
(
,
∘
)
g
↦
ρ
(
g
)
rho:G_1( ,cdot)to G_2( ,circ)\ qquad gmapsto rho(g)
ρ:G1( ,⋅)→G2( ,∘) g↦ρ(g)
∀
g
1
,
g
2
∈
G
∀g1,g2∈G, 有
ρ
(
g
1
⋅
g
2
)
=
ρ
(
g
1
)
∘
ρ
(
g
2
)
rho(g_1cdot g_2)=rho(g_1)circ rho(g_2)
ρ(g1⋅g2)=ρ(g1)∘ρ(g2)成立, 则称
ρ
ρ为群同态(映射).

群同态基本定理
设
ρ
ρ为一个
G
1
G_1
G1到
G
2
G_2
G2的群同态, 则
Ker
ρ
Kerρ是
G
G
G
/
Ker
ρ
≅
Im
ρ
.
G/text{Ker}rhocong text{Im}rho.
第二同构定理
H
<
G
H<G
H<G,
N
⊴
G
N⊴G, 则
H
N
<
G
HN<G
HN<G,
H
∩
N
⊴
H
H∩N⊴H, 且
ρ
:
H
/
H
∩
N
⟶
H
N
/
N
h
(
H
∩
N
)
⟼
h
N
begin{aligned} rho: H/Hcap N&longrightarrow HN/N\ h(Hcap N)&longmapsto hN end{aligned}
ρ:H/H∩Nh(H∩N)⟶HN/N⟼hN
是一个同构.
ρ
~
:
H
⟶
H
N
/
N
h
⟼
h
N
begin{aligned} tilderho: H&longrightarrow HN/N\ h&longmapsto hN end{aligned}
ρ~:Hh⟶HN/N⟼hN
ρ
~
ρ~为满同态, 且
Ker
ρ
~
=
H
∩
N
Kerρ~=H∩N.
先证明
H
N
<
G
HN<G
HN<G, 直接验证集合非空, 满足运算封闭以及有逆元即可.
只需证明H
N
=
N
H
HN=NH
HN=NH,
(
h
)
−
1
=
−
1
h
−
1
∈
N
H
=
H
N
(hn)^{-1}=n^{-1}h^{-1}in NH=HN
(hn)−1=n−1h−1∈NH=HN, 于是
N
⊴
H
N
Nunlhd HN
N⊴HN, 即
H
N
/
N
HN/N
HN/N满足.
H
∩
N
⊴
H
H∩N⊴H,
⟺
∀
h
∈
H
,
h
(
H
∩
N
)
h
−
1
=
H
∩
N
iff forall hin H, h(Hcap N)h^{-1}=Hcap N
⟺∀h∈H,h(H∩N)h−1=H∩N, 因为:
(
h
H
h
−
1
)
∩
(
h
N
h
−
1
)
=
H
∩
N
(hHh^{-1})cap(hNh^{-1})=Hcap N
(hHh−1)∩(hNh−1)=H∩N
Ker
ρ
~
=
H
∩
N
Kerρ~=H∩N.
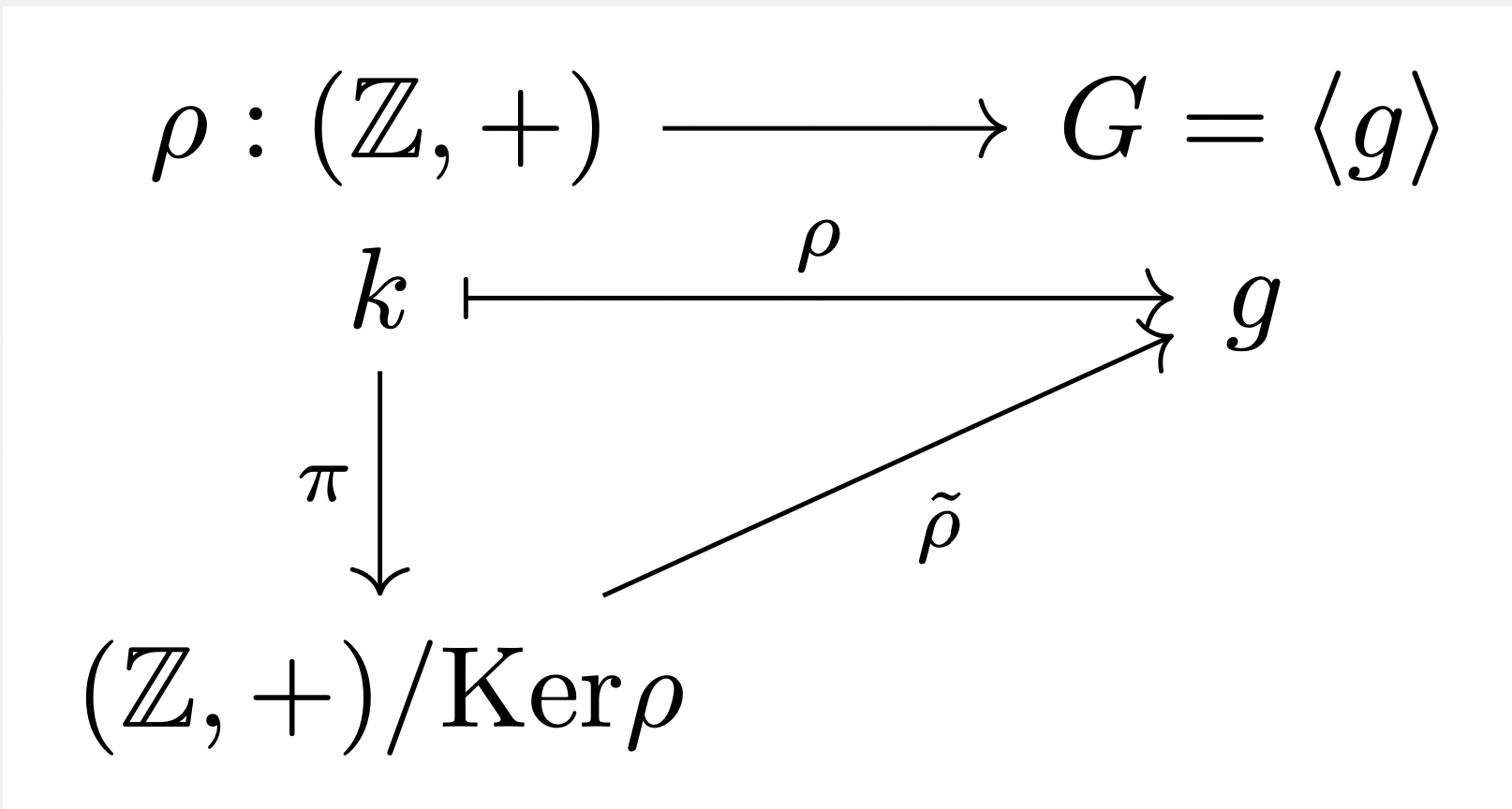
循环群结构定理
n
n
(
Z
/
n
Z
,
+
)
(Z/nZ,+).
有以下群满同态成立:
原文地址:https://blog.csdn.net/qq_41437512/article/details/134748377
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_46806.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!