论文：https://arxiv.org/pdf/1712.01026.pdf
代码：
发表：2018
在计算机视觉的许多领域中，生成对抗性网络已经取得了巨大的成功，其中WGANs系列被认为是最先进的，主要是由于其理论贡献和竞争的定性表现。然而，通过 Wasserstein-1 度量（W-met）来近似 k-Lipschitz约束是非常具有挑战性的。作者提出了一种新的 Wasserstein 散度（W-div），它是W-met的松弛版本，不需要k-Lipschitz约束。
是真数据
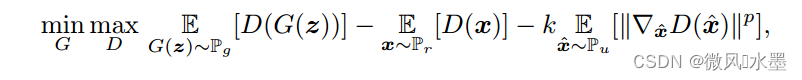
在 WGAN-gp 中，为了满足 1-Lipschitz 约束，训练出好效果，采用了真假数据的插值方法，来模拟全空间的均匀分布 。 WGAN-div 的作者说，这种做法是一种机械性的，很难靠有限的采样，模拟出这种全空间分布。
with a finite number of training iterations on limited input samples, it is very difficult to guarantee the k-Lipschitz constraint for the whole input domain.
作者固定p = 6，测试不同的k，结果为右下角：发现变化不大。FID基本在16附近。
作者固定k = 2，测试不同的p，结果为左下角：发现p=6时取得最优FID数值。
4种设置： ResNet, ResNet without BN, ConvNet, ConvNet without BN
实验结果：ResNet 要好于 ConvNet, 有BN 要好于无BN
参考：
1：Wasserstein Divergence for GANs (WGAN-div) 计算W散度 | 莫烦Python
2：WGAN-div：默默无闻的WGAN填坑者（附开源代码） – 知乎
原文地址:https://blog.csdn.net/lilai619/article/details/134811633
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
如若转载，请注明出处：http://www.7code.cn/show_48076.html
如若内容造成侵权/违法违规/事实不符，请联系代码007邮箱：suwngjj01@126.com进行投诉反馈，一经查实，立即删除！
