POJ 3233 Matrix Power Series 动态规划（矩阵的幂）

本文介绍: 给出一个矩阵A，输出矩阵B的每一项对M取余数的值。

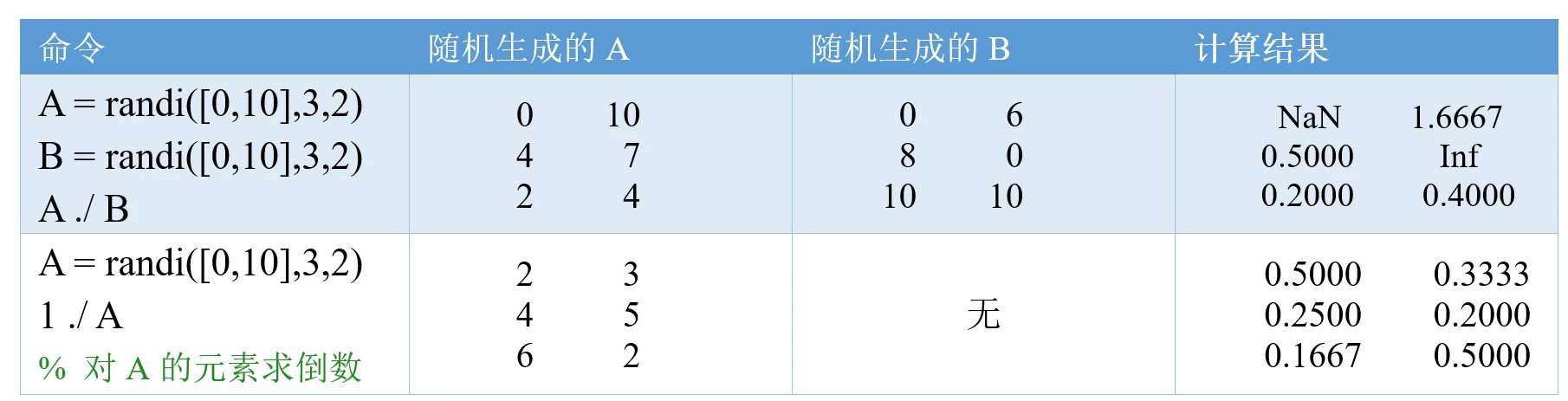
一、题目大意

给出一个矩阵A，

输出矩阵B的每一项对M取余数的值。

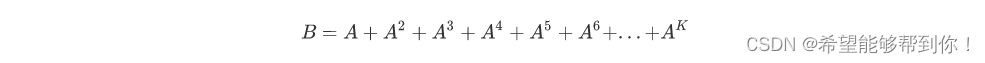
二、解题 思路

以二维矩阵为例，首先计算K=2的情况，我们设结果矩阵为B

有如下表达式

那么不难看出，需要的矩阵其实就是以下的两个矩阵相乘后的左上角的N*N个

然后我们再来考虑K=3的情况，我们设结果矩阵为C

我们来考虑如何把C表示成矩阵B和A相乘的状态。

不难看出C矩阵就是以下两个矩阵相乘后的N*N的左上角

也是如下矩阵的左上角

综上，我们发现计算B和C时，乘号右边的矩阵是相同的，只是我们需要保证前N排的后N列必须始终为A[0][0]..A[0][N-1],A[1][0]..A[1][N-1],…

保留那些值我们可以通过给右边的矩阵右下角放置零矩阵即可。

那么最终题目的答案可以表示成下的表达式。

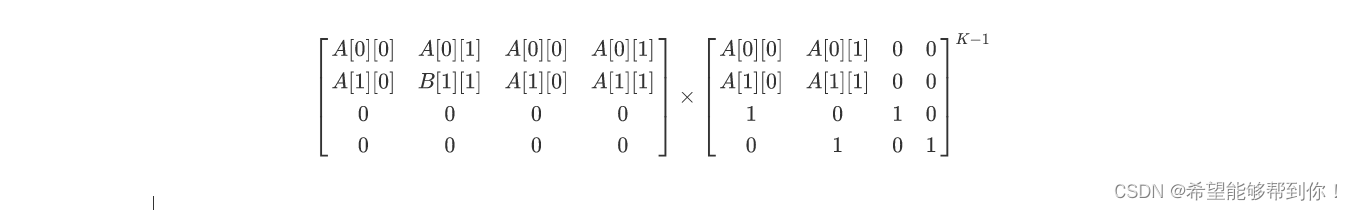
三、代码

#include &lt;iostream&gt;
#include <vector&gt;
using namespace std;
typedef vector<int&gt; vec;
typedef vector<vec&gt; mat;
int M;
mat mul(mat &amp;A, mat &amp;B)
{
    mat C = mat(A.size(), vec(B[0].size()));
    for (int i = 0; i < A.size(); i++)
    {
        for (int j = 0; j < B[0].size(); j++)
        {
            for (int k = 0; k < B.size(); k++)
            {
                C[i][j] = (C[i][j] + A[i][k] * B[k][j]) % M;
            }
        }
    }
    return C;
}
mat pow(mat &amp;A, int N)
{
    mat B = mat(A.size(), vec(A[0].size()));
    for (int i = 0; i < B.size(); i++)
    {
        B[i][i] = 1;
    }
    while (N &gt; 0)
    {
        if (N &amp; 1)
        {
            B = mul(B, A);
        }
        A = mul(A, A);
        N &gt;&gt;= 1;
    }
    return B;
}
void solve()
{
    int N, K;
    scanf("%d%d%d", &amp;N, &amp;K, &amp;M);
    mat A = mat(2 * N, vec(2 * N));
    for (int i = 0; i < N; i++)
    {
        for (int j = 0; j < N; j++)
        {
            scanf("%d", &amp;A[i][j]);
        }
    }
    for (int i = 0; i < N; i++)
    {
        A[i + N][i] = 1;
        A[i + N][i + N] = 1;
    }
    mat B = mat(2 * N, vec(2 * N));
    for (int i = 0; i < N; i++)
    {
        for (int j = 0; j < N; j++)
        {
            B[i][j] = A[i][j];
            B[i][j + N] = A[i][j];
        }
    }
    A = pow(A, K - 1);
    A = mul(B, A);
    for (int i = 0; i < N; i++)
    {
        for (int j = 0; j < N; j++)
        {
            printf("%d%c", A[i][j] % M, j + 1 == N ? 'n' : ' ');
        }
    }
}
int main()
{
    solve();
    return 0;
}