python笔记：dtaidistance

本文介绍: 最快的版本（比其他版本快30至300倍）直接使用C语言编写，但需要数组作为输入（使用双精度类型），并且（可选地）通过将max _dist 设置为欧几里得距离的上界来剪枝计算。这个其实和我们前面的war ping _path是一样的。距离函数具有线性空间复杂度但二次时间复杂度。可以将ds转化成上三角矩阵的值，节省空间。输入为一个列表的列表。

1 介绍

用于DTW的库
纯Py th on 实现和更快的C语言实现

2 DTW举例

2.1 绘制 war ping 路径

from dtaidistance import dtw
from dtaidistance import dtw_visualisation as dtwvis
import numpy as np
import matplotlib.pyplot as plt

s1 = np.array([0., 0, 1, 2, 1, 0, 1, 0, 0, 2, 1, 0, 0])
s2 = np.array([0., 1, 2, 3, 1, 0, 0, 0, 2, 1, 0, 0, 0])
path=dtw.warping_path(s1,s2)
dtwvis.plot_warping(s1,s2,path)

path
'''
[(0, 0),
 (1, 0),
 (2, 1),
 (3, 2),
 (3, 3),
 (4, 4),
 (5, 5),
 (6, 5),
 (7, 6),
 (8, 7),
 (9, 8),
 (10, 9),
 (11, 10),
 (11, 11),
 (12, 12)]
'''

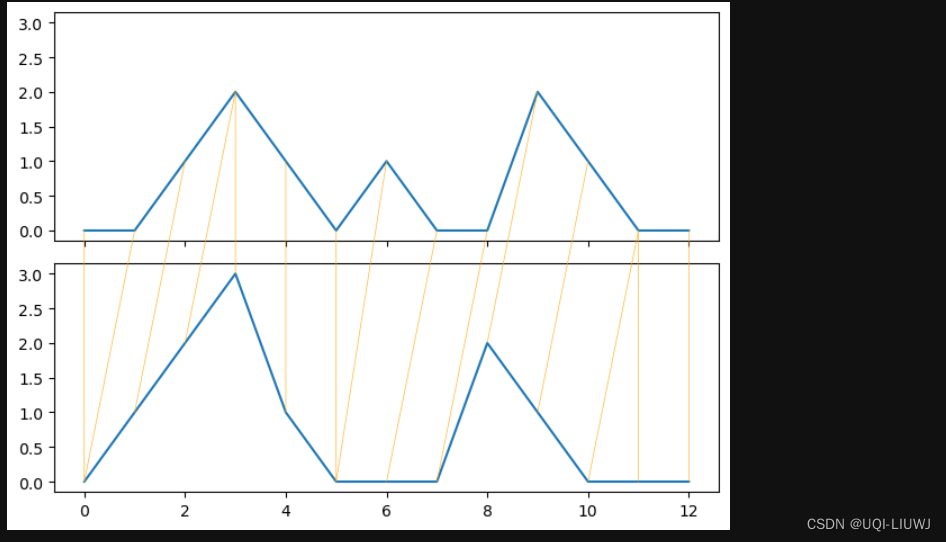
2.2 计算 dtw 距离

s1 = np.array([0., 0, 1, 2, 1, 0, 1, 0, 0, 2, 1, 0, 0])
s2 = np.array([0., 1, 2, 3, 1, 0, 0, 0, 2, 1, 0, 0, 0])
dtw.distance(s1,s2)
#1.4142135623730951

2.3 快速 版本 计算 dt w 距离

最快的版本（比其他版本快30至300倍）直接使用C语言编写，但需要数组作为输入（使用双精度类型），并且（可选地）通过将max _dist 设置为欧几里得距离的上界来剪枝计算

s1 = np.array([0., 0, 1, 2, 1, 0, 1, 0, 0, 2, 1, 0, 0])
s2 = np.array([0., 1, 2, 3, 1, 0, 0, 0, 2, 1, 0, 0, 0])
dtw.distance_fast(s1,s2)
#1.4142135623730951

s1 = np.array([0., 0, 1, 2, 1, 0, 1, 0, 0, 2, 1, 0, 0])
s2 = np.array([0., 1, 2, 3, 1, 0, 0, 0, 2, 1, 0, 0, 0])
dtw.distance_fast(s1,s2,use_pruning=True)
#1.4142135623730951

2.4 降低DTW 复杂度

距离函数具有线性空间复杂度但二次时间复杂度。

为了降低时间复杂度，有多种选择可用。
- 在DTW实现中最常用的方法是使用一个窗口，表示允许的最大偏移量
  - 这将复杂度降低到窗口大小和最长序列长度的乘积
  - window 参数：仅允许偏移量最多为此值远离两条对角线
- 其他一些选项用于提前停止动态规划算法正在探索的某些或所有路径
  - max_di st：避免计算将大于此值的部分路径。如果找不到小于或等于此值的解决方案，则返回无穷大
  - use_pr uni n g：一种剪枝部分路径的好方法是将最大距离设置为欧几里得上界
  - max_length_diff:果两个序列的长度差大于此值，则返回无穷大

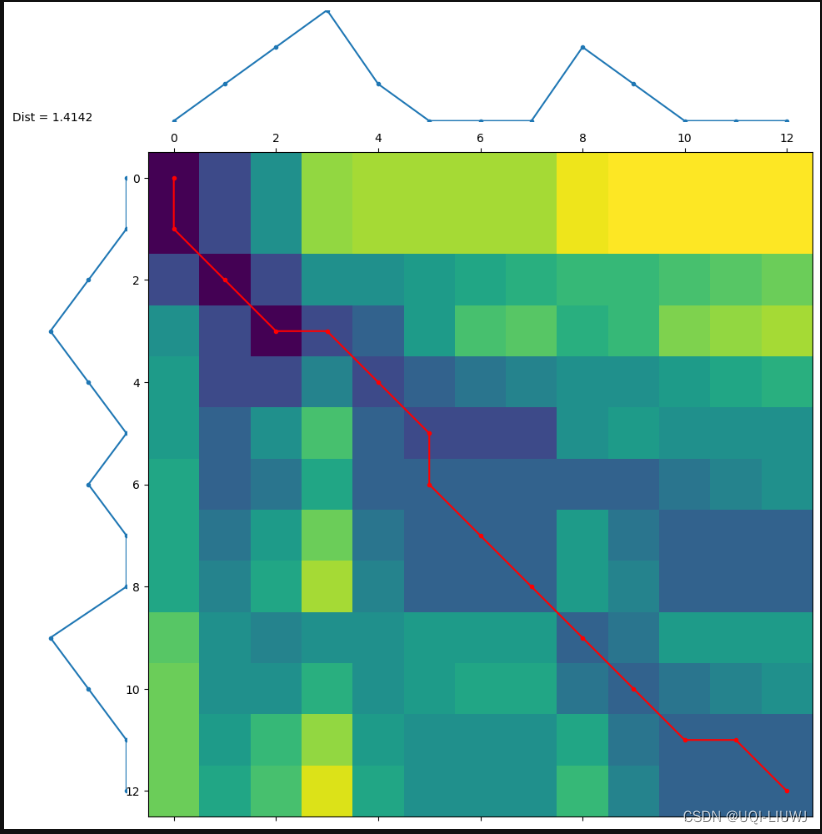
2.5 得到累计成本 矩阵并绘制之

s1 = np.array([0., 0, 1, 2, 1, 0, 1, 0, 0, 2, 1, 0, 0])
s2 = np.array([0., 1, 2, 3, 1, 0, 0, 0, 2, 1, 0, 0, 0])
distance,matrix=dtw.warping_paths(s1,s2)
distance
#1.4142135623730951

matrix.shape
#(14, 14)

2.5.1 求最佳路径

dtw.best_path(matrix)
'''
[(0, 0),
 (1, 0),
 (2, 1),
 (3, 2),
 (3, 3),
 (4, 4),
 (5, 5),
 (6, 5),
 (7, 6),
 (8, 7),
 (9, 8),
 (10, 9),
 (11, 10),
 (11, 11),
 (12, 12)]
'''

这个其实和我们前面的warpin g_pat h是一样的

dtw.warping_path(s1,s2)
'''
dtw.warping_path(s1,s2)
'''

2.5.2 可视化 结果

dtwvis.plot_warpingpaths(s1,s2,matrix,dtw.warping_path(s1,s2))

2.6 多个时间序列的DTW

要计算列表中所有序列之间的DTW距离度量，可以使用dtw.distance_matrix方法
用dtw.distance_matrix_fast方法可以加速计算，该方法试图在C语言环境中运行所有算法

from dtaidistance import dtw
import numpy as np
timeseries = [
    np.array([0, 0, 1, 2, 1, 0, 1, 0, 0], dtype=np.double),
    np.array([0.0, 1, 2, 0, 0, 0, 0, 0, 0, 0, 0]),
    np.array([0.0, 0, 1, 2, 1, 0, 0, 0])]
ds = dtw.distance_matrix(timeseries)
ds
'''
array([[0.        , 1.41421356, 1.        ],
       [1.41421356, 0.        , 1.        ],
       [1.        , 1.        , 0.        ]])
'''

输入为一个列表的列表

2.6.1 compact=True

可以将ds转化成上三角矩阵的值，节省空间

from dtaidistance import dtw
import numpy as np
timeseries = [
    np.array([0, 0, 1, 2, 1, 0, 1, 0, 0], dtype=np.double),
    np.array([0.0, 1, 2, 0, 0, 0, 0, 0, 0, 0, 0]),
    np.array([0.0, 0, 1, 2, 1, 0, 0, 0])]
ds = dtw.distance_matrix(timeseries,compact=True)
ds
#array('d', [1.4142135623730951, 1.0, 1.0])