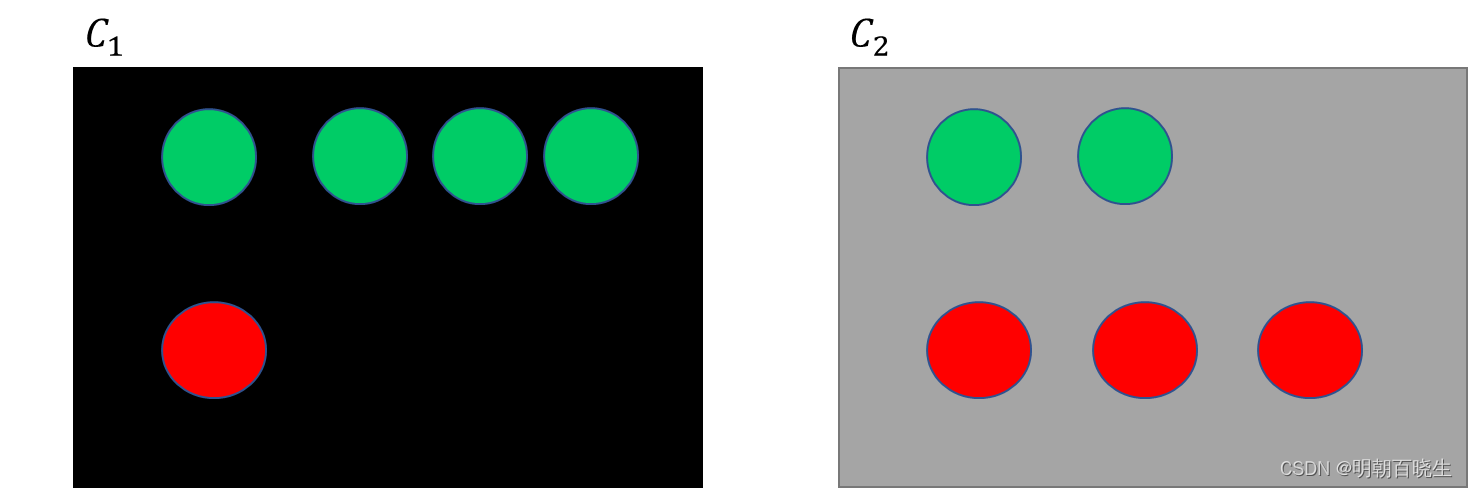
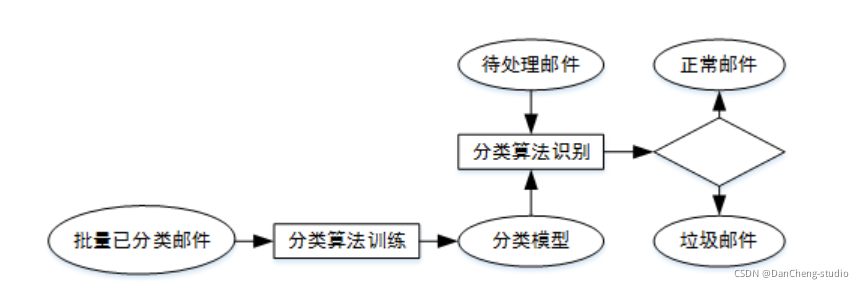
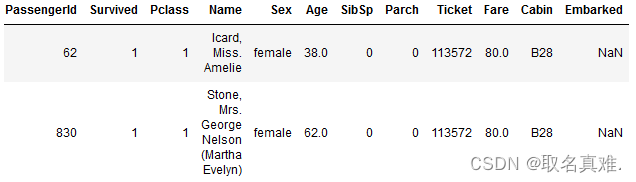
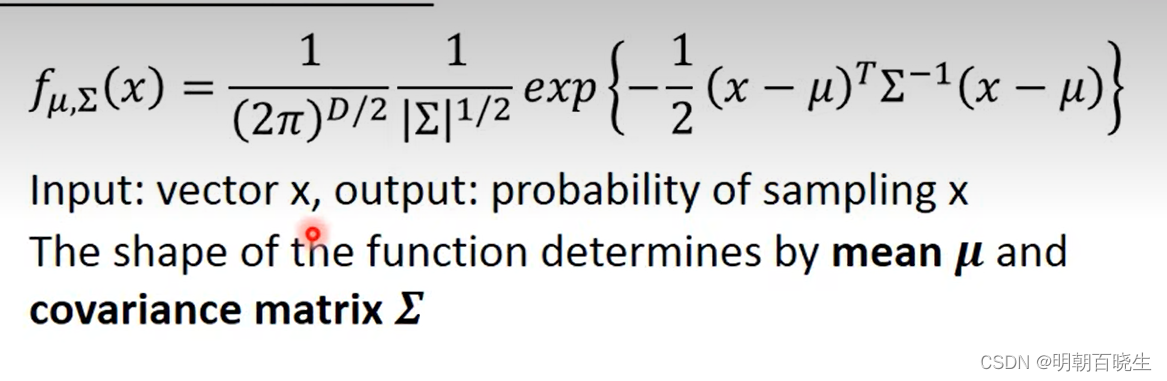[PyTorch][chapter 5][李宏毅深度学习][Classification]

互联网 11 月前 0 4

本文介绍: 为了降低过拟合，通常假设不同类别的方差一样,均值不同. 通过增加样本数降低方差。高斯分类器第一步要得到均值,和方差。均值,方差如何获取？这个值就是样本均值和样本的协方差，假设有79个点。这章节主要讲解常用的分类器原理.分类主要是要找到一个映射函数。主要应用场景：垃圾邮件分类,手写数字识别,金融信用评估.不同均值,方差的高斯分类器容易发生过拟合.假设不同类别服从不同的高斯分布。有两个盒子,里面分别放绿球和红球。: 条件概率,不同类别中出现 x的概率。: 不同类别出现的概率，先验概率。

这章节主要讲解常用的分类器原理.分类主要是要找到一个映射函数

$c=f(x)$ 比如垃圾邮件分类 :

c=0, 垃圾邮件 c=1 正常邮件

主要应用场景：垃圾邮件分类,手写数字识别,金融信用评估.

这里面简单了解一下，很少用

1： Ge n er a ti v e model

2: 高斯分类器

3: 高斯分类器跟其它模型关系

一 Ge n er a ti v e model

朴素贝叶斯分类器：

以二分类为例：

$c_1,c_2$ 不同类别

$p(c_1),p(c_2)$ : 不同类别出现的概率，先验概率

$p(x|c_1),p(x|c_2)$ : 条件概率,不同类别中出现 x的概率

$p(c_1 |x)=frac{p(x)p(x|c_1)}{p(x|c_1)p(c_1)+p(x|c_2)p(c_2)}$ (贝叶斯联合分布推导)

有两个盒子,里面分别放绿球和红球

现在有个绿色的球,它来自哪个盒子

$p(c_1|g)=frac{p(g|c_1)p(c_1)}{p(g)}$

其中 $p(g)=p(c_1)p(g|c_1)+p(c_2)p(g|c_2)$

$=frac{2}{3}frac{4}{5}+frac{1}{3}frac{2}{5}$

所以

$p(c_1|g)=frac{4}{5}$

$p(c_c|g)=1-frac{4}{5}=frac{1}{5}$

二高斯分类器

假设不同类别服从不同的高斯分布

输入 x ,输出对该类别的概率

$sum$ : 协方差矩阵

a = np.cov(x,y)

2.2 主要流程

2.3 maximum like li h o od 极大似然估计（计算 u, $sum$ ）

高斯分类器第一步要得到均值,和方差。均值,方差如何获取？

我们通过极大似然估计计算均值和协方差矩阵

我们有训练样本 $(x^1,c_1),(x^2,c_1),(x^3,c_1).....(x^N,c_1)$

我们要找到 $u,sum$ 使得下面概率最大

$L(u,sum)=f_{u,sum}(x^1)=f_{u,sum}(x^2)...f_{u,sum}(x^N)$

这个值就是样本均值和样本的协方差，假设有79个点

2.3 高斯分类器问题

不同均值,方差的高斯分类器容易发生过拟合.

为了降低过拟合，通常假设不同类别的方差一样,均值不同. 通过增加样本数降低方差。如下图两类样本.

$L(u_1,u_2,sum)=f_{u_1,sum}(x^1)f_{u_1,sum}(x^2)...f_{u_2,sum}(x^{80})...f_{u_2,sum}(x^{179})$

三高斯分类器跟其它模型关系

1：跟Si gm o id 关系

设 $z=ln frac{p(x|c_1)p(c_1)}{p(x|c_2)p(c_2)}$

则

$p(c_1|x)=frac{p(x|c_1)p(c_1)}{p(x|c_1)p(c_1)+p(x|c_2)p(c_2)}$

$=frac{1}{1+frac{p(x|c_2)p(c_2)}{p(x|c_1)p(c_1)}}$

$=frac{1}{1+e^{-z}}$

$=sigma (z)$

3.2 跟Linear 函数的关系

$z=lnfrac{p(x|c_1)}{p(x|c_2)}+lnfrac{p(c_1)}{p(c_2)}$

$=lnfrac{p(x|c_1)}{p(x|c_2)}+lnfrac{N_1}{N_2}$

当 $sum^2=sum^1=sum$ 时候,可以进一步简化

$z=(u_1-u_2)^T(sum)^{-}x-frac{1}{2}u_1^Tsum^{-}u_1+frac{1}{2}u_2^Tsum^{-}u_2+lnfrac{N_1}{N_2}$

非x 的项可以看作常数 b

x项前面可以看作w

z=wx+b

原文地址:https://blog.csdn.net/chen g x f2/ar ti cle/detail s/134785877

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。

如若转载，请注明出处：http://www.7code.cn/show_48726.html

如若内容造成侵权/违法违规/事实不符，请联系代码007邮箱：su w n gjj01@126.com进行投诉反馈，一经查实，立即删除！

声明：本站所有文章，如无特殊说明或标注，均为本站原创发布。任何个人或组织，在未征得本站同意时，禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益，可联系我们进行处理。

分类器均值方差

相关文章

opencv#30 线性滤波

互联网 10 月前 4

大创项目推荐题目：垃圾邮件(短信)分类算法实现机器学习深度学习开题

大创项目推荐题目：垃圾邮件(短信)分类算法实现机器学习深度学习开题

互联网 10 月前 4

四个模型建模及数据分析整理（基于Titanic数据集）

四个模型建模及数据分析整理（基于Titanic数据集）

互联网 10 月前 4

Python–使用布林线设计均值回归策略

Python–使用布林线设计均值回归策略

python 12 月前 2

微调Fine tune

互联网 12 月前 2

利用Python进行调查问卷的信度检验和效度检验，并对量表进行因子分析

利用Python进行调查问卷的信度检验和效度检验，并对量表进行因子分析

python 12 月前 5

JVM之GC垃圾回收

互联网 9 月前 3

行为型设计模式—中介者模式

互联网 9 月前 4

发表回复取消回复