数学建模之拟合及其代码

本文介绍: 发现新天地，欢迎访问Cr不是铬的。

发现新天地，欢迎访问Cr不是铬的个人网站

引言

与插值问题不同，在拟合问题中不需要曲线一定经过给定的点。拟合问题的目标是寻求一个函数（曲线），使得该曲线在某种准则下与所有的数据点最为接近，即曲线拟合的最好（最小化损失函数）

最小二乘法

在一维线性拟合中，采用的是最小二乘法来求得最优拟合。

file

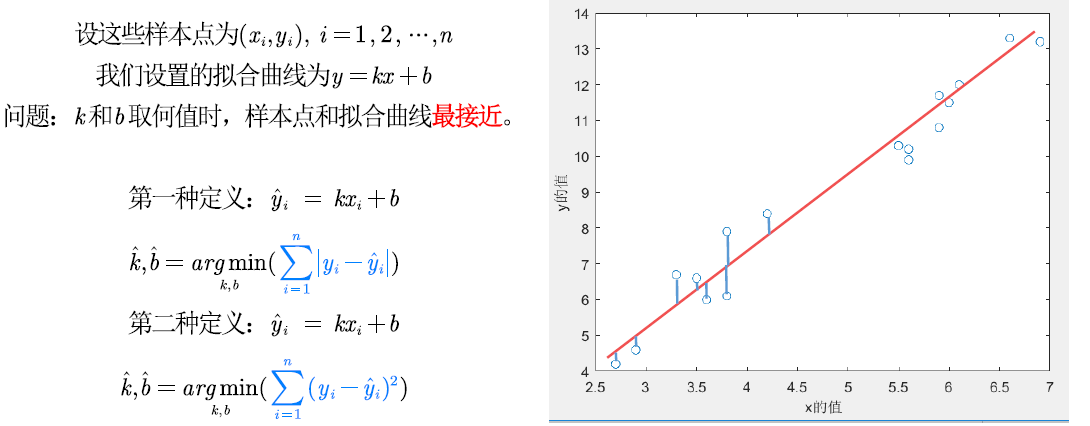
求解过程证明:

file

拟合好坏的评价

通过最小二乘法确定拟合方程后，怎么来评价拟合的好坏呢？

SST：总体平方和
SSE：误差平方和
SSR: 回归平方和

file

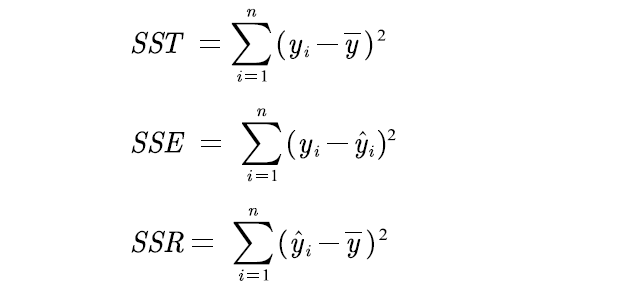
SST = SSE + SSR;

拟合优度:1 – SSE/SST.

R^2越接近1，说明误差平方和越接近0，误差越小说明拟合的越好

代码部分

最小二乘

%% 开始拟合
%行数
n = size(x,1);
%计算拟合参数
k = (n*sum(x.*y) - sum(y)*sum(x))/(n*sum(x.^2)-sum(x)*sum(x));
b = (sum(x.^2)*sum(y)-sum(x)*sum(x.*y))/(n*sum(x.^2)-sum(x)*sum(x));

hold on % 继续在之前的图形上来画图形
grid on % 显示网格线
% % 画出y=kx+b的函数图像 plot(x,y)
% % 传统的画法：模拟生成x和y的序列，比如要画出[0,5]上的图形
% xx = 2.5: 0.1 :7 ; % 间隔设置的越小画出来的图形越准确
% yy = k * xx + b;  % k和b都是已知值
% plot(xx,yy,'-')

file

匿名函数 用法

% 匿名函数的基本用法。
% handle = @(arglist) anonymous_function
% 其中handle为调用匿名函数时使用的名字。
% arglist为匿名函数的输入参数，可以是一个，也可以是多个，用逗号分隔。
% anonymous_function为匿名函数的表达式。
% 举个小例子
%  z=@(x,y) x^2+y^2; 
%  z(1,2) 
% % ans =  5
% fplot函数可用于画出匿名一元函数的图形。
% fplot(f,xinterval) 将匿名函数f在指定区间xinterval绘图。xinterval =  [xmin xmax] 表示定义域的范围

% f=@(x) k*x+b;
% fplot(f,[2.5,7]);

file

拟合优度

%% 求拟合度
y_hat = k*x+b; % y的拟合值
SSR = sum((y_hat-mean(y)).^2)  % 回归平方和
SSE = sum((y_hat-y).^2) % 误差平方和
SST = sum((y-mean(y)).^2) % 总体平方和
SST-SSE-SSR   % 5.6843e-14  =   5.6843*10^-14   matlab浮点数计算的一个误差
R_2 = SSR / SST

完整代码

%% 导入数据
load data
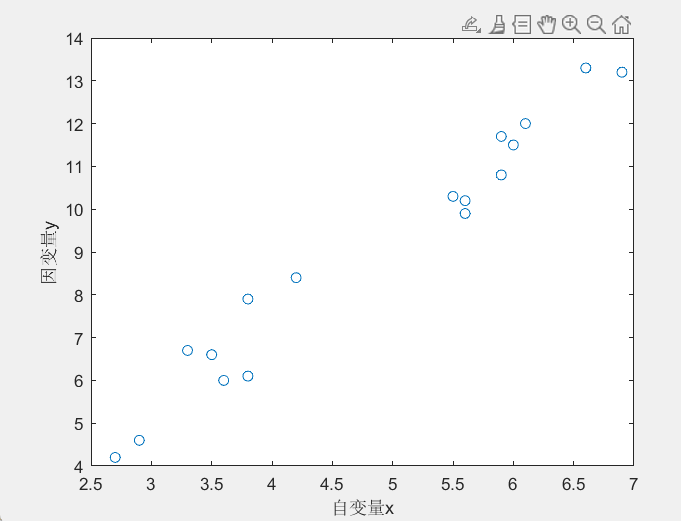
%绘制原始散点图
plot(x,y,'o')
%给x轴与y轴加上标签
xlabel('自变量x')
ylabel('因变量y')
%% 开始拟合
%行数
n = size(x,1);
%计算拟合参数
k = (n*sum(x.*y) - sum(y)*sum(x))/(n*sum(x.^2)-sum(x)*sum(x));
b = (sum(x.^2)*sum(y)-sum(x)*sum(x.*y))/(n*sum(x.^2)-sum(x)*sum(x));

hold on % 继续在之前的图形上来画图形
grid on % 显示网格线
% % 画出y=kx+b的函数图像 plot(x,y)
% % 传统的画法：模拟生成x和y的序列，比如要画出[0,5]上的图形
% xx = 2.5: 0.1 :7 ; % 间隔设置的越小画出来的图形越准确
% yy = k * xx + b;  % k和b都是已知值
% plot(xx,yy,'-')

% 匿名函数的基本用法。
% handle = @(arglist) anonymous_function
% 其中handle为调用匿名函数时使用的名字。
% arglist为匿名函数的输入参数，可以是一个，也可以是多个，用逗号分隔。
% anonymous_function为匿名函数的表达式。
% 举个小例子
%  z=@(x,y) x^2+y^2; 
%  z(1,2) 
% % ans =  5
% fplot函数可用于画出匿名一元函数的图形。
% fplot(f,xinterval) 将匿名函数f在指定区间xinterval绘图。xinterval =  [xmin xmax] 表示定义域的范围

% f=@(x) k*x+b;
% fplot(f,[2.5,7]);

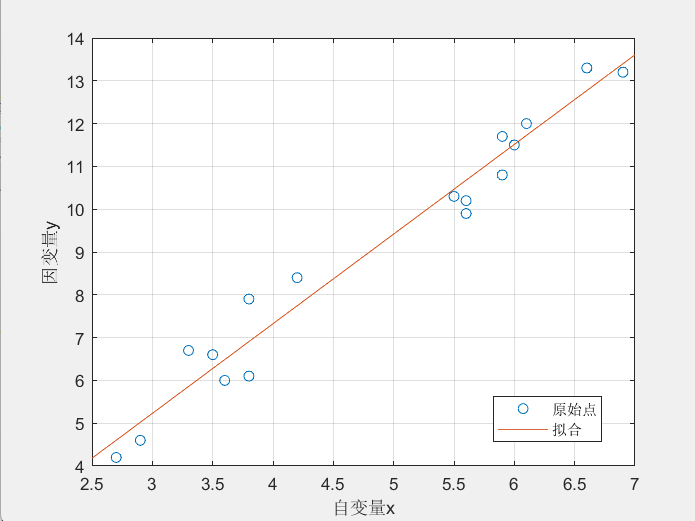
f = @(x) k*x + b;
fplot(f,[2.5,7.0])
legend('原始点','拟合')
%% 求拟合度
y_hat = k*x+b; % y的拟合值
SSR = sum((y_hat-mean(y)).^2)  % 回归平方和
SSE = sum((y_hat-y).^2) % 误差平方和
SST = sum((y-mean(y)).^2) % 总体平方和
SST-SSE-SSR   % 5.6843e-14  =   5.6843*10^-14   matlab浮点数计算的一个误差
R_2 = SSR / SST