神经网络 模型表示
模型表示一
为了构建神经网络模型，我们需要首先思考大脑中的神经网络是怎样的？每一个神经元都可以被认为是一个处理单元/神经核（processing unit/Nucleus），它含有许多输入/树突（input/Dendrite），并且有一个输出/轴突（output/Axon）。神经网络是大量神经元相互链接并通过电脉冲来交流的一个网络。
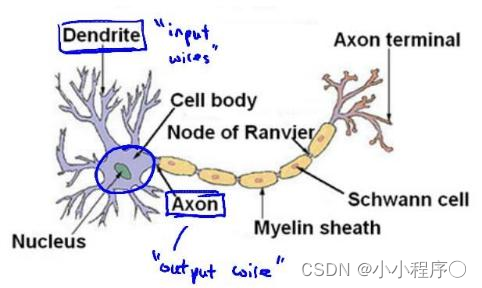
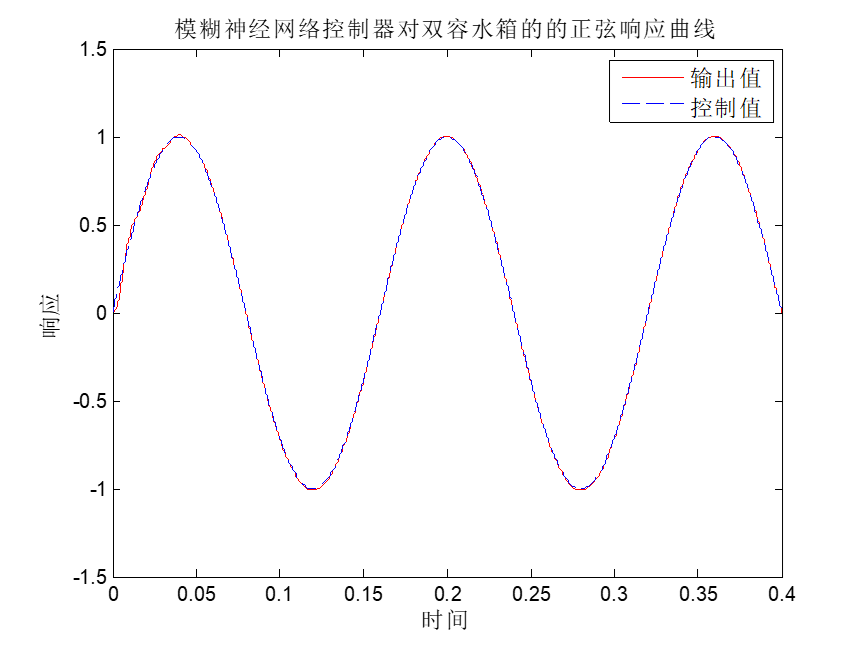
下面是一组神经元的示意图，神经元利用微弱的电流进行沟通。这些弱电流也称作动作电位，其实就是一些微弱的电流。所以如果神经元想要传递一个消息，它就会就通过它的轴突，发送一段微弱电流给其他神经元，这就是轴突。
这里是一条连接到输入神经，或者连接另一个神经元树突的神经，接下来这个神经元接收这条消息，做一些计算，它有可能会反过来将在轴突上的自己的消息传给其他神经元。这就是所有人类思考的模型：我们的神经元把自己的收到的消息进行计算，并向其他神经元传递消息。这也是我们的感觉和肌肉运转的原理。如果你想活动一块肌肉，就会触发一个神经元给你的肌肉发送脉冲，并引起你的肌肉收缩。如果一些感官：比如说眼睛想要给大脑传递一个消息，那么它就像这样发送电脉冲给大脑的。
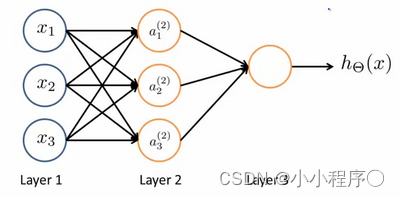
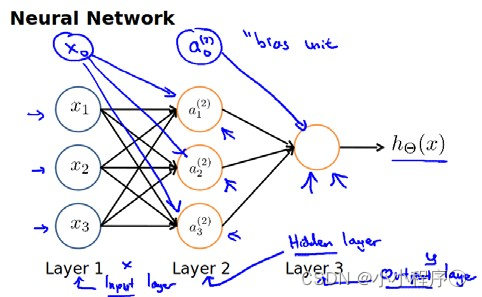
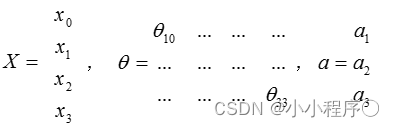
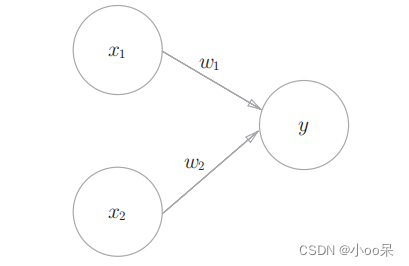
神经网络模型建立在很多神经元之上，每一个神经元又是一个个学习模型。这些神经元（也叫激活单元，activation unit）采纳一些特征作为输出，并且根据本身的模型提供一个输出。下图是一个以逻辑回归模型作为自身学习模型的神经元示例，在神经网络中，参数又可被成为权重（weight）。
其中
1
x1,
2
x2,
x
3
x_3
x3是输入单元（input units），我们将原始数据输入给它们。
1
a_1
a1,
2
a_2
a2,
a
3
a_3
a3是中间单元，它们负责将数据进行处理，然后呈递到下一层。
最后是输出单元，它负责计算
θ
(
x
)
hθ(x)。
神经网络模型是许多逻辑单元按照不同层级组织起来的网络，每一层的输出变量都是下一层的输入变量。下图为一个3层的神经网络，第一层成为输入层（Input Layer），最后一层称为输出层（Output Layer），中间一层成为隐藏层（Hidden Layers）。我们为每一层都增加一个偏差单位（bias unit）
a
(
j
)
j
j
j 层的第
θ
(
j
)
θ(j)代表从第
j
j
θ
(
1
)
θ(1)代表从第一层映射到第二层的权重的矩阵。其尺寸为：以第
j
+
1
j+1
j
j
j 层的激活单元数加一为列数的矩阵。例如：上图所示的神经网络中
θ
(
1
)
θ(1)的尺寸为 3*4。
a
1
(
2
)
=
(
Θ
10
(
1
)
x
0
+
Θ
11
(
1
)
x
1
+
Θ
12
(
1
)
x
2
+
Θ
13
(
1
)
x
3
)
a_{1}^{(2)}=g(Theta _{10}^{(1)}{{x}_{0}}+Theta _{11}^{(1)}{{x}_{1}}+Theta _{12}^{(1)}{{x}_{2}}+Theta _{13}^{(1)}{{x}_{3}})
a1(2)=g(Θ10(1)x0+Θ11(1)x1+Θ12(1)x2+Θ13(1)x3)
a
2
(
2
)
=
(
Θ
20
(
1
)
x
0
+
Θ
21
(
1
)
x
1
+
Θ
22
(
1
)
x
2
+
Θ
23
(
1
)
x
3
)
a_{2}^{(2)}=g(Theta _{20}^{(1)}{{x}_{0}}+Theta _{21}^{(1)}{{x}_{1}}+Theta _{22}^{(1)}{{x}_{2}}+Theta _{23}^{(1)}{{x}_{3}})
a2(2)=g(Θ20(1)x0+Θ21(1)x1+Θ22(1)x2+Θ23(1)x3)
a
3
(
2
)
=
g
(
Θ
30
(
1
)
x
0
+
Θ
31
(
1
)
x
1
+
Θ
32
(
1
)
x
2
+
Θ
33
(
1
)
x
3
)
a_{3}^{(2)}=g(Theta _{30}^{(1)}{{x}_{0}}+Theta _{31}^{(1)}{{x}_{1}}+Theta _{32}^{(1)}{{x}_{2}}+Theta _{33}^{(1)}{{x}_{3}})
a3(2)=g(Θ30(1)x0+Θ31(1)x1+Θ32(1)x2+Θ33(1)x3)
h
Θ
(
x
)
=
g
(
Θ
10
(
2
)
a
0
(
2
)
+
Θ
11
(
2
)
a
1
(
2
)
+
Θ
12
(
2
)
a
2
(
2
)
+
Θ
13
(
2
)
a
3
(
2
)
)
{{h}_{Theta }}(x)=g(Theta _{10}^{(2)}a_{0}^{(2)}+Theta _{11}^{(2)}a_{1}^{(2)}+Theta _{12}^{(2)}a_{2}^{(2)}+Theta _{13}^{(2)}a_{3}^{(2)})
hΘ(x)=g(Θ10(2)a0(2)+Θ11(2)a1(2)+Θ12(2)a2(2)+Θ13(2)a3(2))
上面进行的讨论中只是将特征矩阵中的一行（一个训练实例）喂给了神经网络，我们需要将整个训练集都喂给我们的神经网络算法来学习模型。
我们可以知道：每一个
a
a
a都是由上一层所有的
x
x
x和每一个
x
x
x所对应的决定的。
（我们把这样从左到右的算法称为前向传播算法( FORWARD PROPAGATION )）
把
x
x
x,
θ
θ,
a
a
我们可以得到
θ
⋅
X
=
a
θ⋅X=a 。
原文地址:https://blog.csdn.net/2201_75381449/article/details/134750791
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
如若转载，请注明出处：http://www.7code.cn/show_49553.html
如若内容造成侵权/违法违规/事实不符，请联系代码007邮箱：suwngjj01@126.com进行投诉反馈，一经查实，立即删除！
