本文介绍: 可以看到现在我们要可以用,拉格朗日乘数法,将 有等式约束条件的优化问题 转换为 无约束优化问题,把有条件转换为无条件对吧,但是我们的SVM支持向量机的目标函数中,的条件是不等式条件对吧,不是等式,所以更复杂一些.可以看到通过,拉格朗日乘数法来构造,拉格朗日函数L(x,lamada),然后让L(x,lamada)对未知数和lamada进行求导,得到一组方程式,就可以计算x和lamada的结果。然后我们对L(x,lamada)这个公式中的,对x的导数为0,对lamada导数也为0,求出x,lamada。

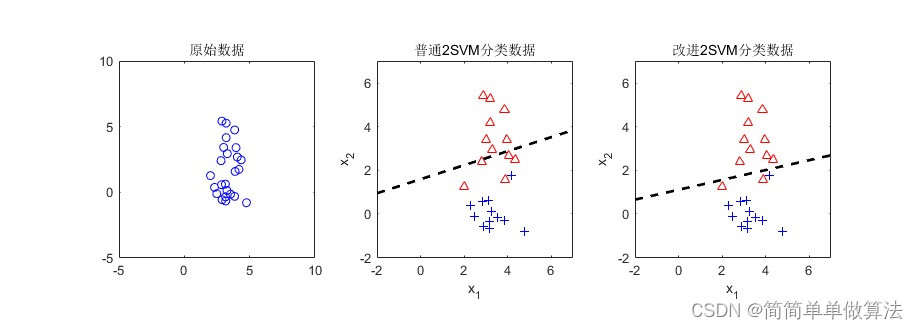
上一节我们已经演示了把SVM支持向量机的分割线,画出来,并且,我们也推导了SVM支持向量机的公式,但是支持向量机的公式,是带有条件的对吧,带有条件就算起来比较麻烦
可以看到现在我们要可以用,拉格朗日乘数法,将 有等式约束条件的优化问题 转换为 无约束优化问题,把有条件转换为无条件对吧,但是我们的SVM支持向量机的目标函数中,的条件是不等式条件对吧,不是等式,所以更复杂一些.

可以看到,下面这个就是minf(x) s.t h(x) = 0 这个就是拉格朗日乘数法,可以看到
这个意思就是说,在h(x) = 0的条件下,来求min f(x)对吧 最小值对吧.
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。