第五章 数理统计的基础知识
由于大量随机现象必然呈现出它的规律性,故理论上只要对随机现象进行足够多次的观察,研究对象的规律性就一定能清楚地呈现出来,但实际上人们常常无法对所研究的对象的全体(或总体)进行观察,而只能抽取其中的部分(或样本)进行观察或试验以获得有限的数据.
5.1 数理统计的基本概念
一、总体与总体分布
在数理统计中,把研究的问题所涉及的对象的全体所组成的集合称为总体(或母体).把构成总体的每一个成员(或元素)称为个体.总体中所包含的个体的数量称为总体的容量.容量为有限的称为有限总体;容量为无限的称为无限总体.总体与个体之间的关系,即集合与元素之间的关系
定义1:统计学中称随机变量(或向量)X为总体,并把随机变量(或向量)的分布称为总体分布
二、样本与样本分布
六、统计量
七、常用统计量
以下设X1,X2,…,Xn为总体X的一个样本.
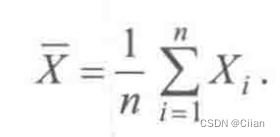
3.样本标准差

4.样本(k阶)原点矩
5.样本(k阶)中心矩
5.2 常用的统计分布
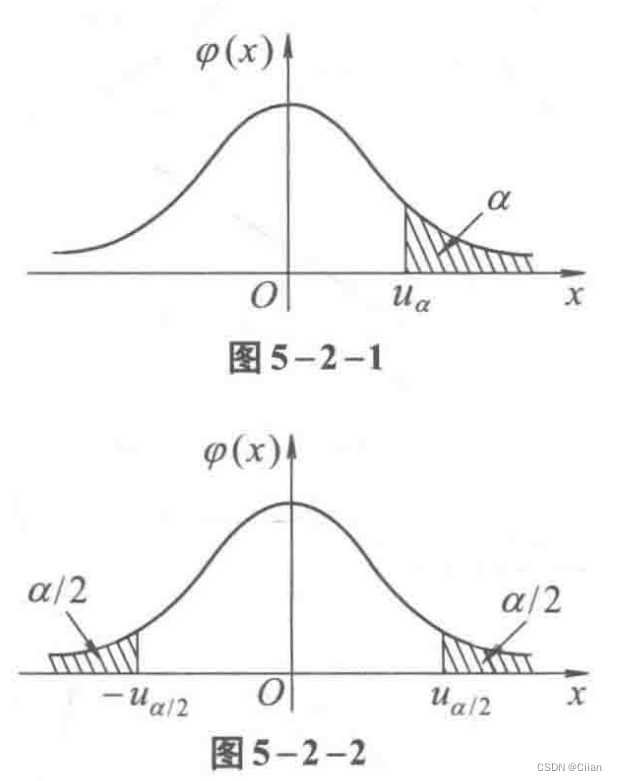
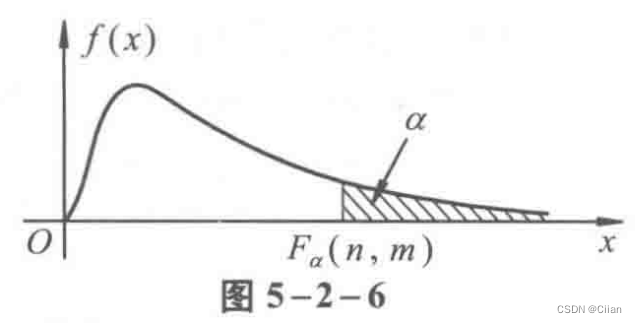
一、分位数
二、
x2分布
三、t分布
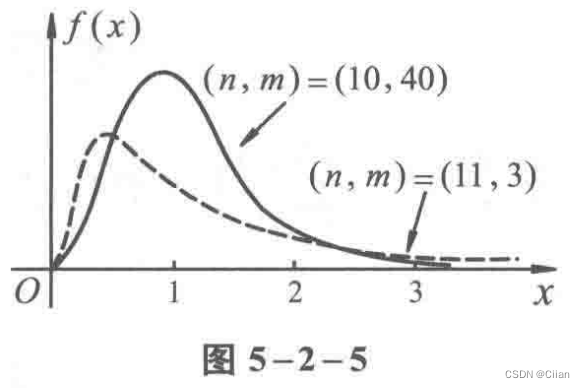
四、F分布
5.3抽样分布(第六章基础)
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。

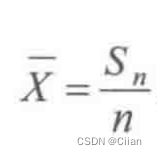
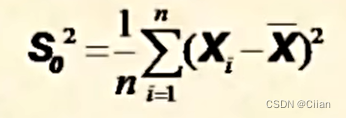
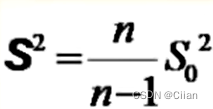
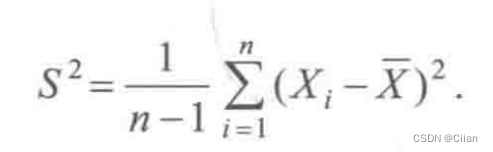
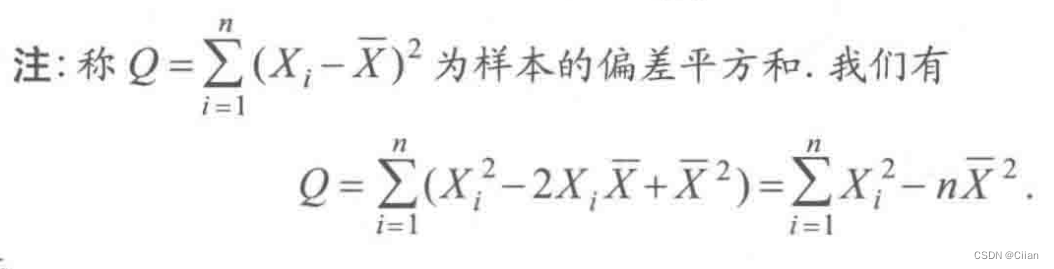
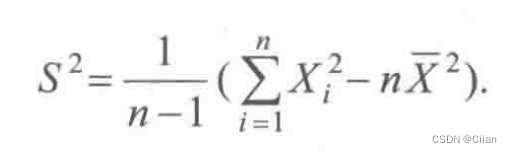
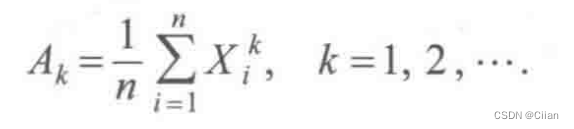
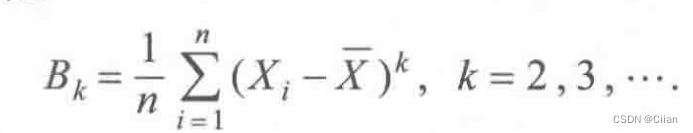
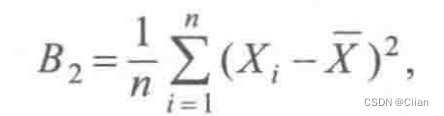


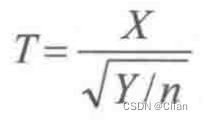
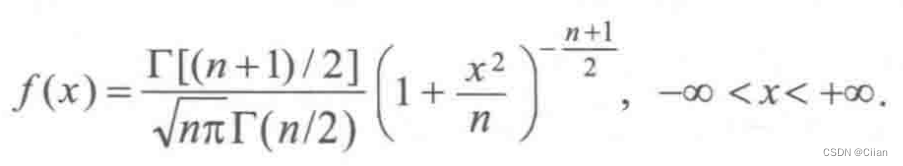 (偶
(偶
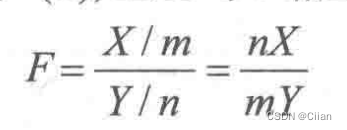
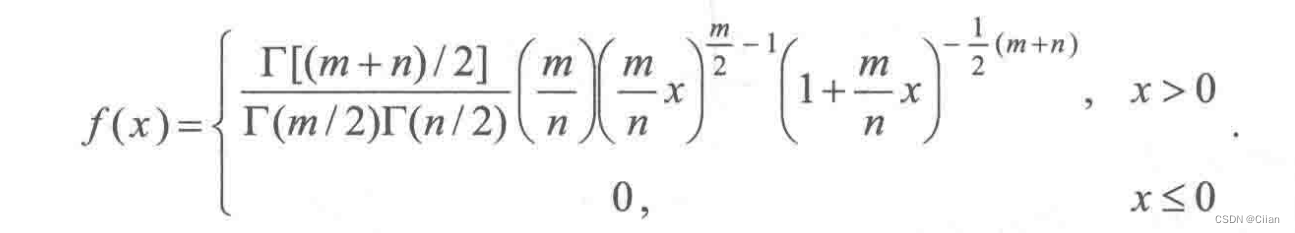
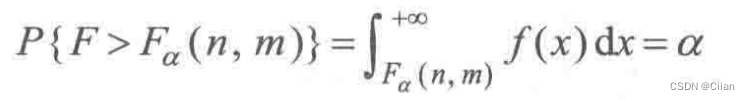

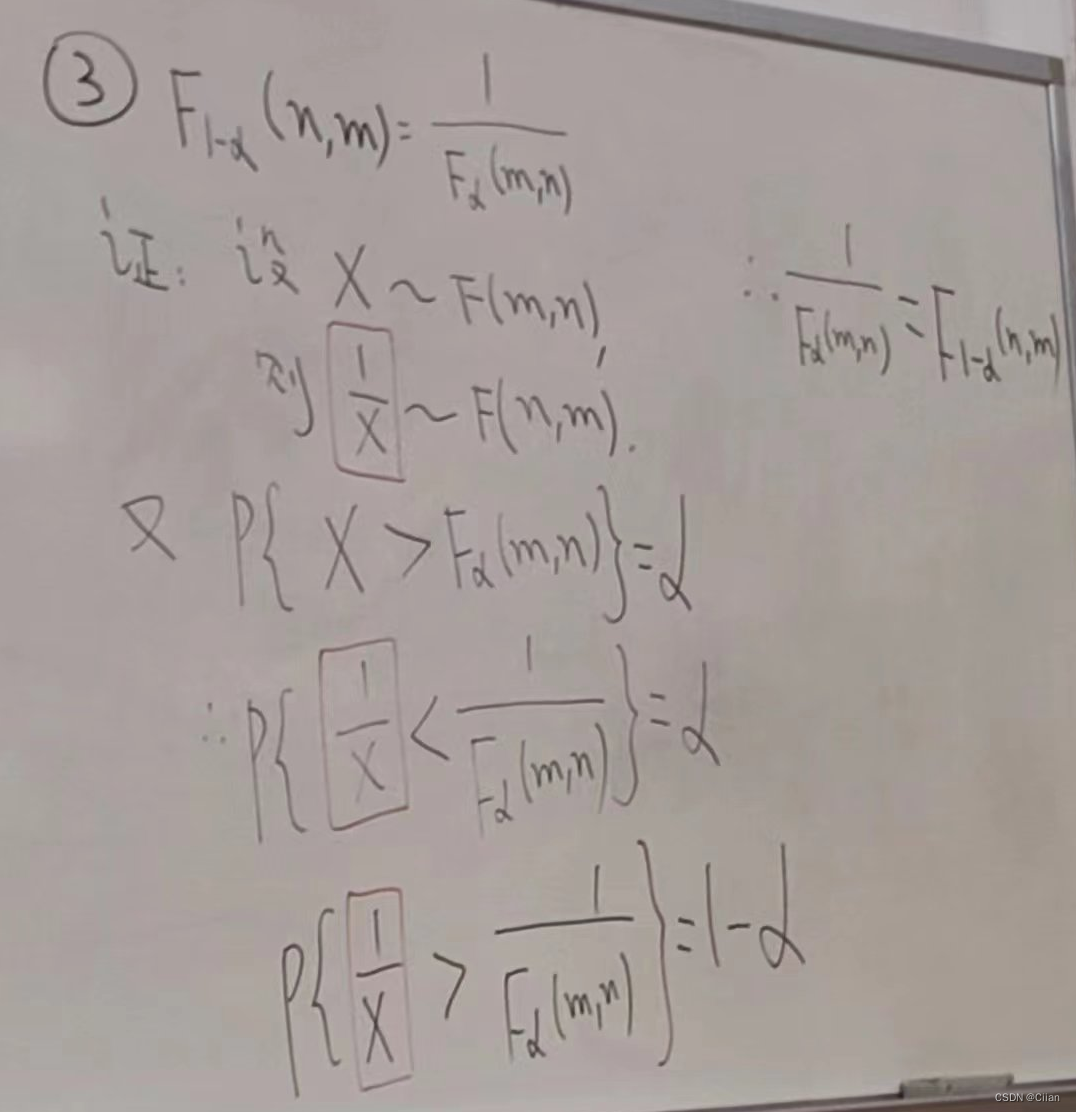
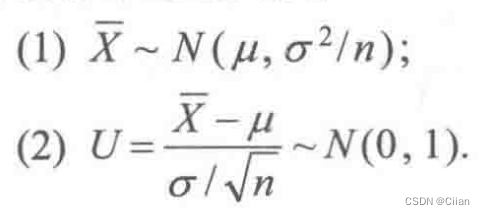
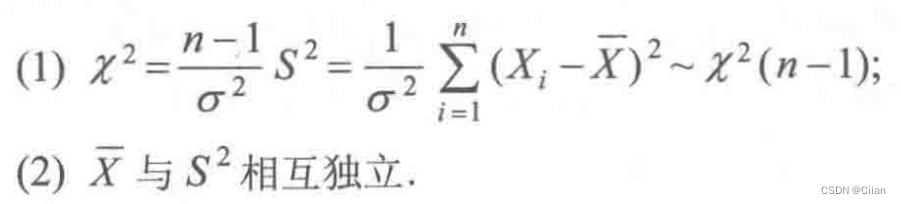
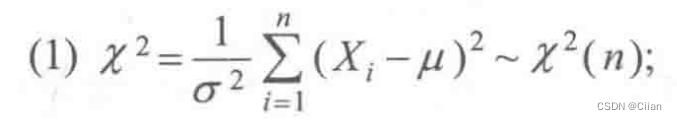
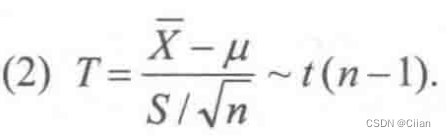

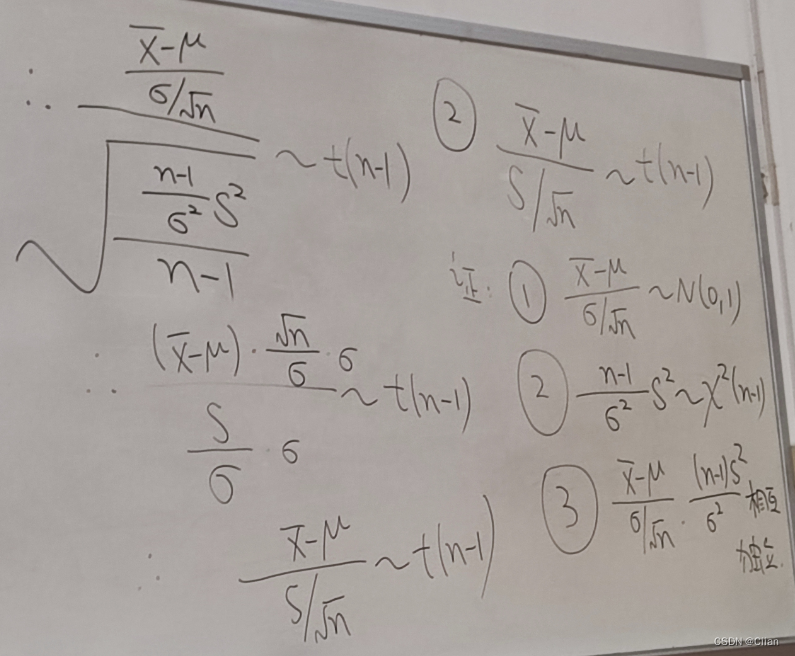



![[软件工具]文档页数统计工具软件pdf统计页数word统计页数ppt统计页数图文打印店快速报价工具](https://img-blog.csdnimg.cn/direct/09dfbaff3e9a47a9a551dd65fef5d482.jpeg)