本文介绍: 队列(queue)是一种遵循先入先出规则的线性数据结构。顾名思义,队列模拟了排队现象,即新来的人不断加入队列的尾部,而位于队列头部的人逐个离开。如下图所示,我们将队列的头部称为“队首”,尾部称为“队尾”,将把元素加入队尾的操作称为“入队”,删除队首元素的操作称为“出队”。
队列(queue)是一种遵循先入先出规则的线性数据结构。顾名思义,队列模拟了排队现象,即新来的人不断加入队列的尾部,而位于队列头部的人逐个离开。
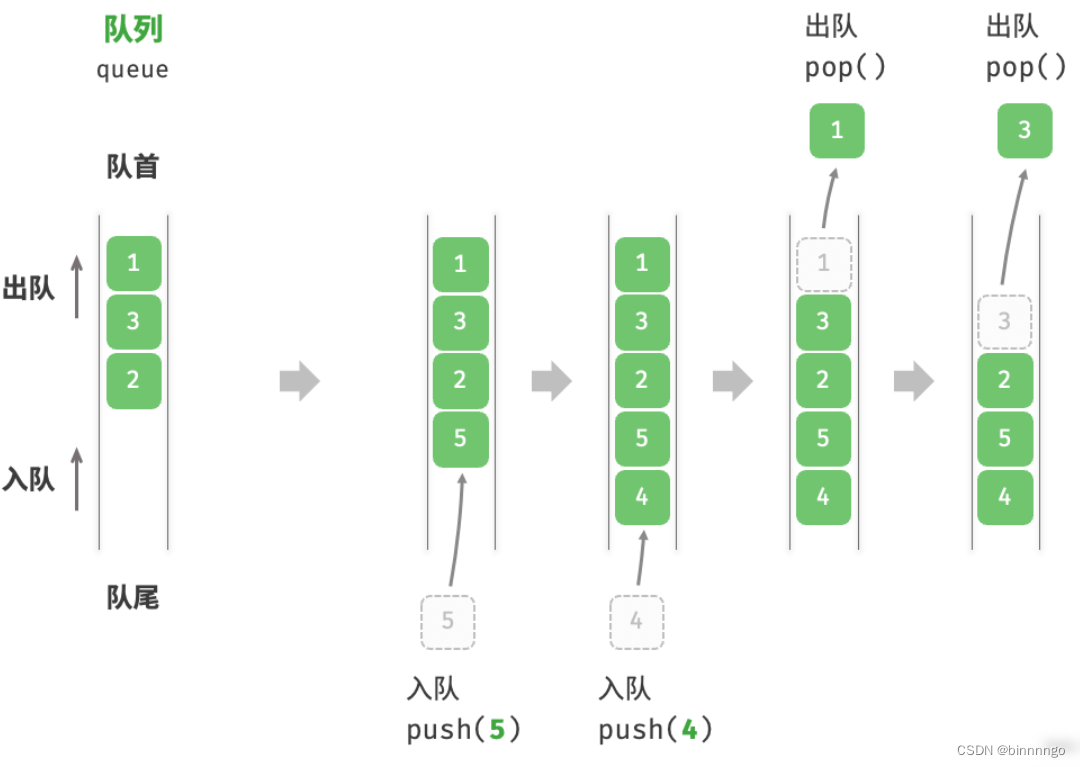
如下图所示,我们将队列的头部称为“队首”,尾部称为“队尾”,将把元素加入队尾的操作称为“入队”,删除队首元素的操作称为“出队”。
8.1 队列常用操作
队列的常见操作如下表所示。需要注意的是,不同编程语言的方法名称可能会有所不同。我们在此采用与栈相同的方法命名。

8.2 队列实现
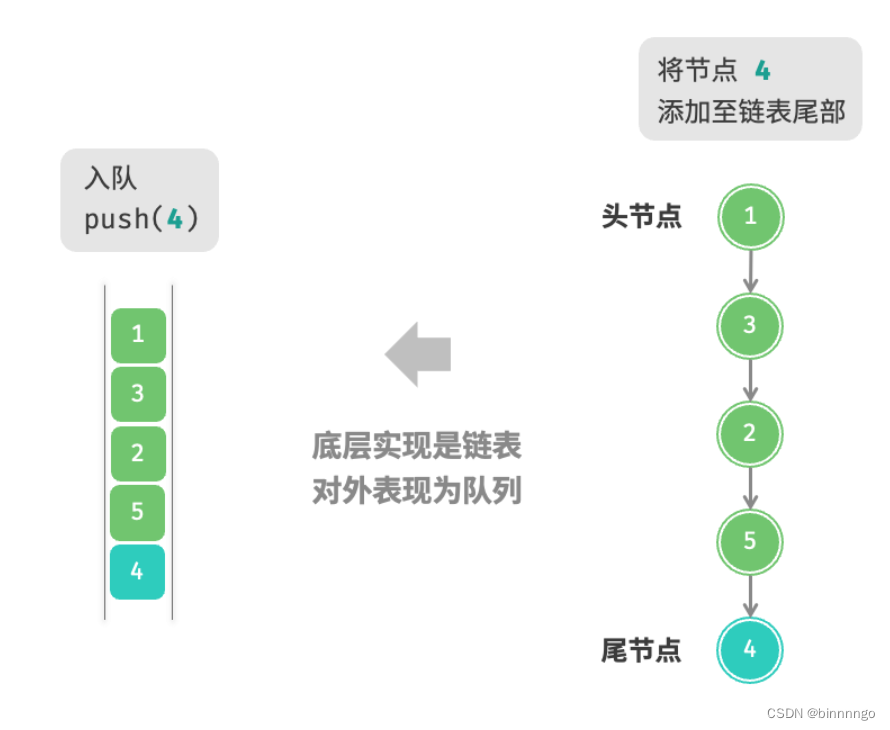
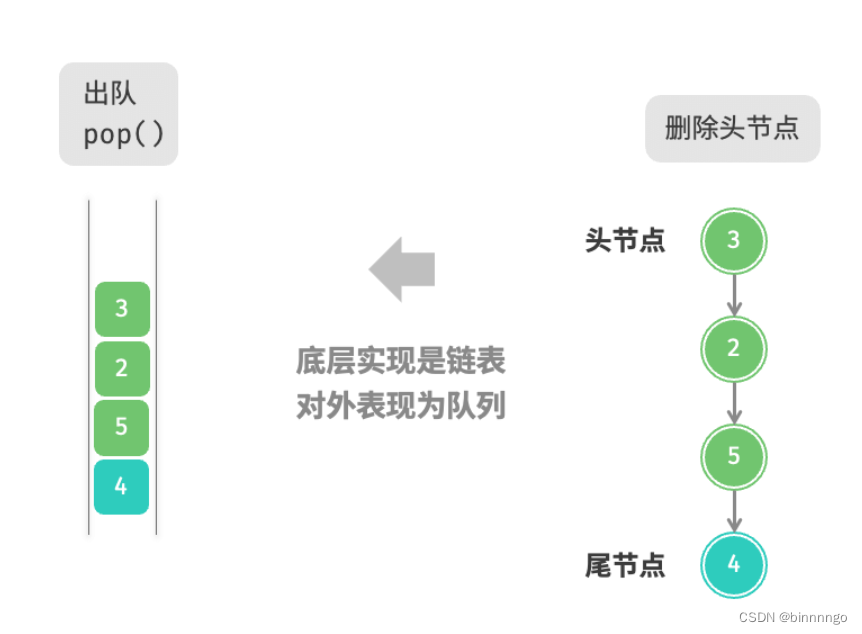
1. 基于链表的实现
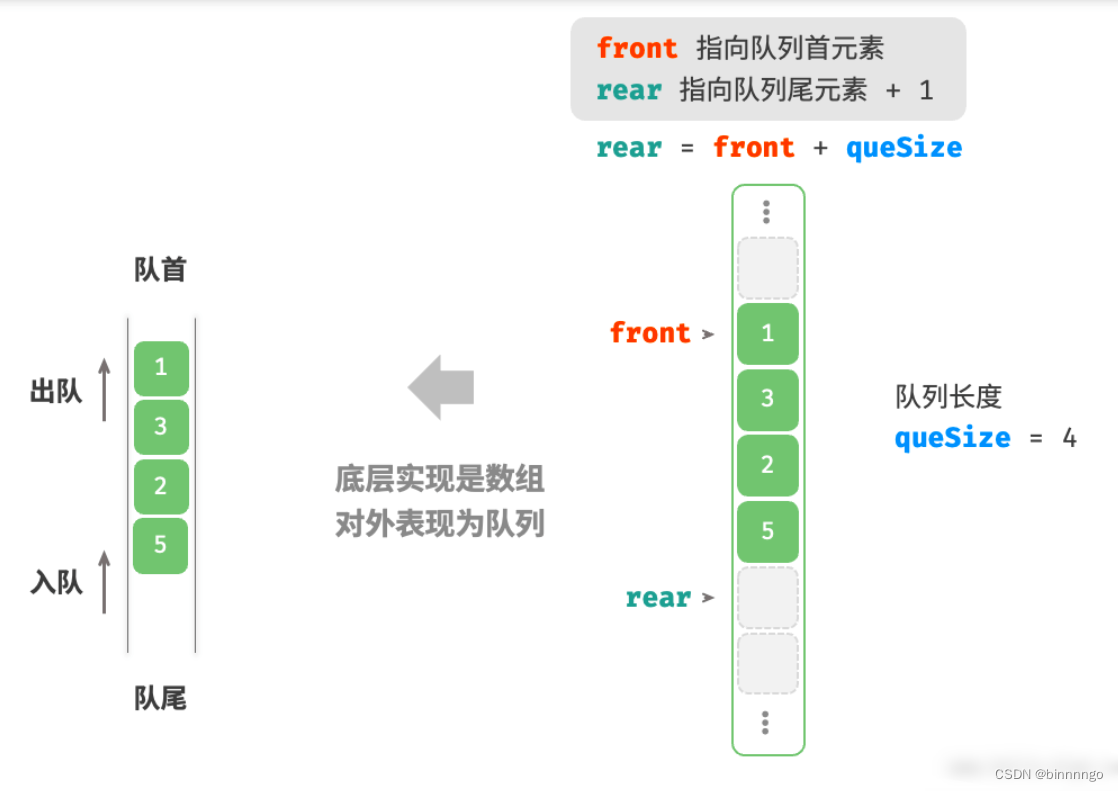
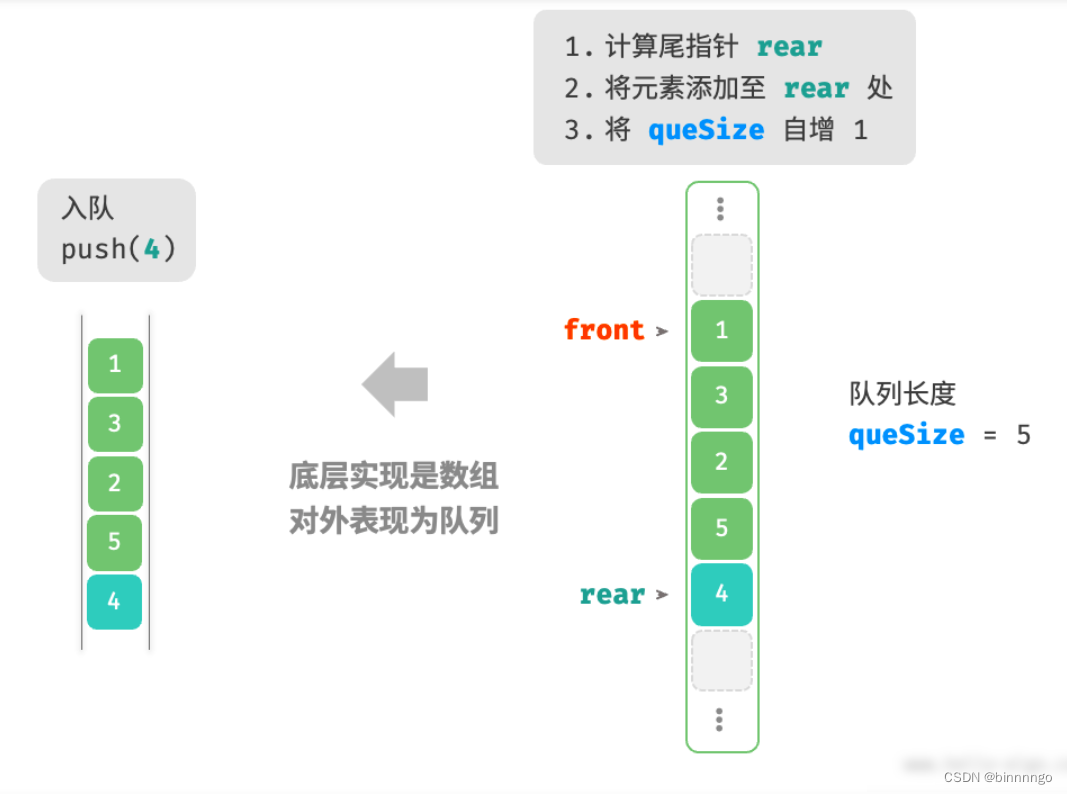
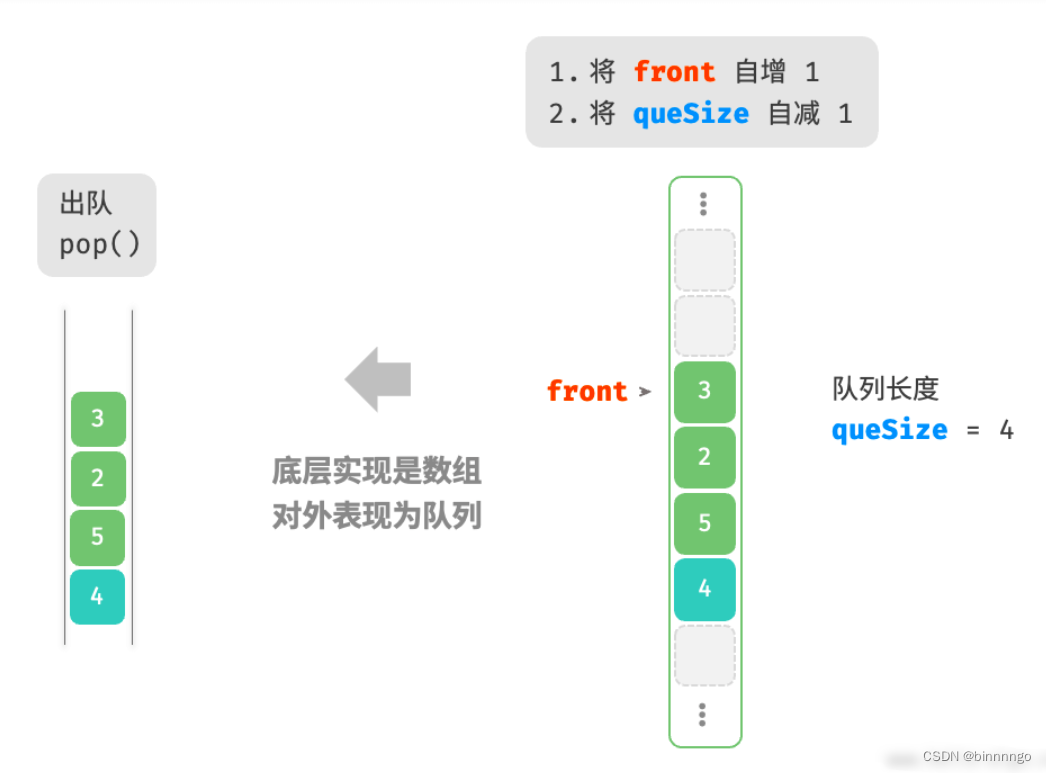
2. 基于数组的实现
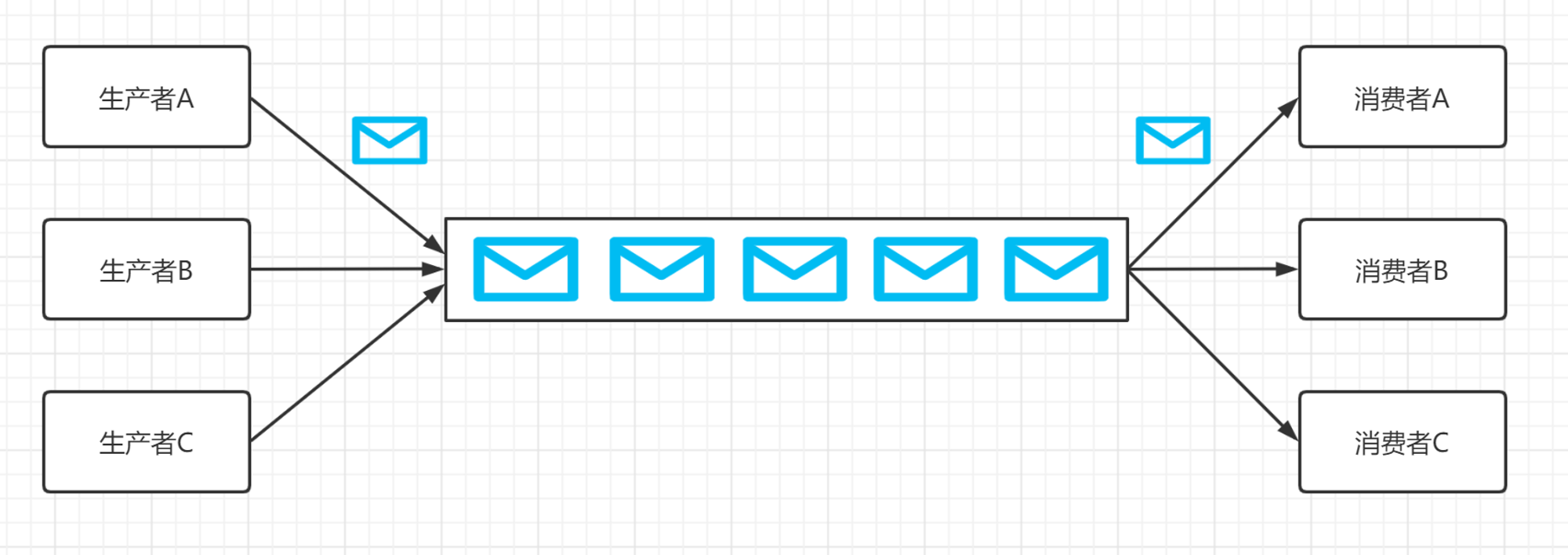
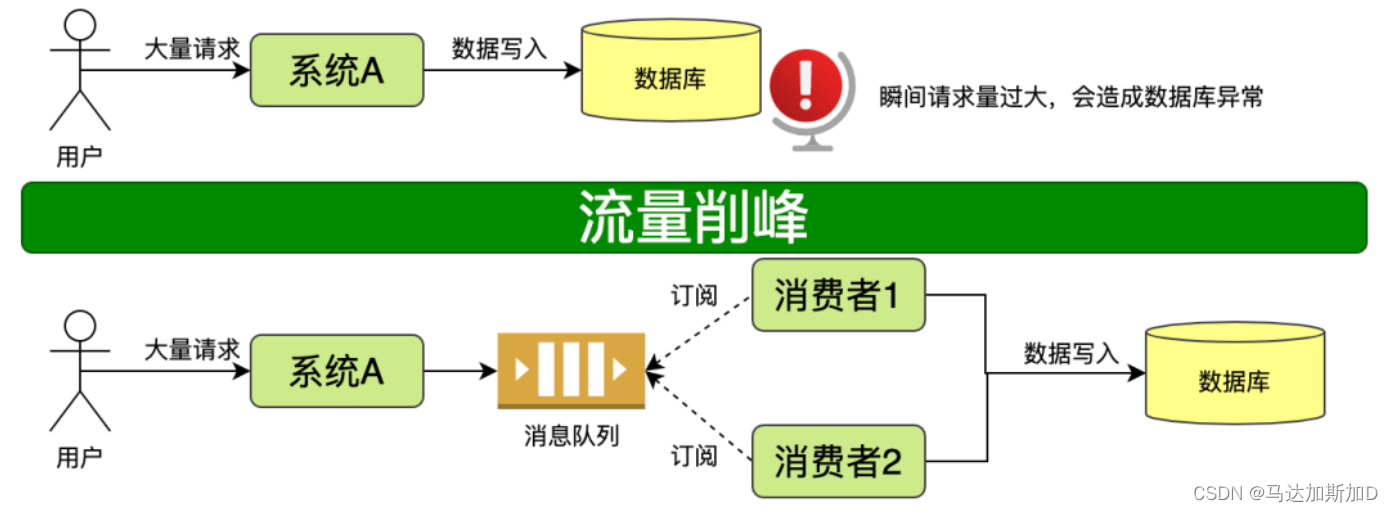
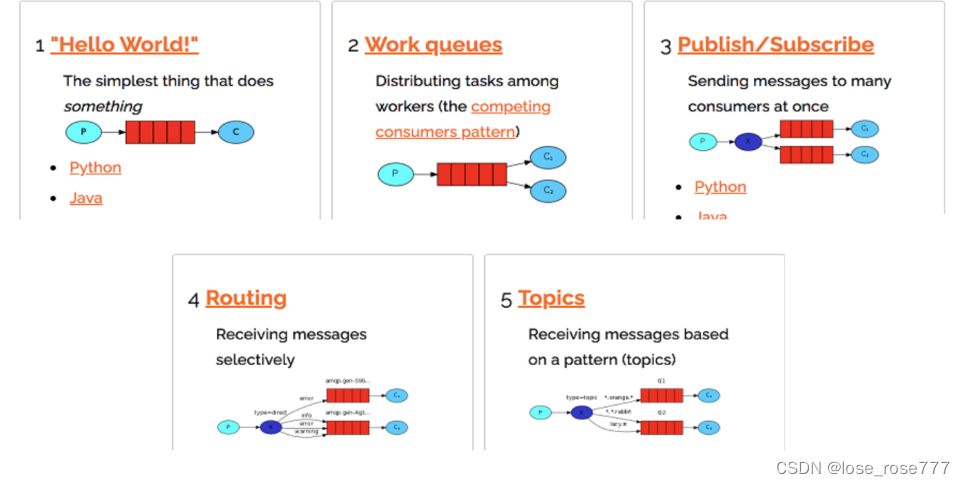
8.3 队列典型应用
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。