基础算法–搜索与图论（1）

本文介绍: 对于一个序列，对应图上每条边都是起点在终点前面易知，如果存在环的话，就一定不存在拓扑序列所以，有向无环图又被称为拓扑图入度为0的点可以作为起点，所以，拓扑排序步骤如下：把所有入度为0的点入队。

文章目录

DFS和BFS
- DFS搜索应用
- - n-皇后问题
树和图的存储
DFS遍历
BFS遍历
- 应用
- - 拓扑排序

DFS和BFS

DFS，深度优先搜索，
- 数据结构：stack
- 空间：Oh
- 不具有最短性
BFS，宽度优先搜索
- queue
- O2^h
- 具有最短性（当图的所有边权重都是相同的时，bfs搜到的一定是最短路，只有这时候才能用bfs求最短路，一般情况下都用最短路算法求最短路，最短路算法的时间复杂度比较高）

DFS搜索应用

n-皇后问题

将n个皇后放到n*n的棋盘上，使任意两个皇后不能在同一行，同一列，同一斜线上

解法一：

按照全排列方式解，一行一行的放，放的时候保证同一列，同一斜线都没有其他皇后（由于是按行放的，同一行一定没有其他皇后），放完标记这一列，这一斜线有皇后，直到把n行都放完，不断向前回溯，找新的放法

public class Main{
    static final int N = 20;
    static char[][]q = new char[N][N];
    static boolean[]col = new boolean[N];
    static boolean[]dg = new boolean[N];//斜线 y = x + b
    static boolean[]udg = new boolean[N];//反斜线 y = -x + b
    static int n;
    
    static void dfs(int u) {
        if(u == n) {
            for(int i = 0;i < n;i++) {
                for(int j = 0;j < n;j++) System.out.print(q[i][j]);
                System.out.println();
            }
            System.out.println();
        }else {
            for(int i = 0;i < n;i++) {
                if(!col[i] && !dg[u + i] && !udg[u - i + n]) {//这里udg  +n是为了防止索引为负数
                    q[u][i] = 'Q';
                    col[i] = dg[u+i] = udg[u - i + n] = true;
                    dfs(u + 1);
                    col[i] = dg[u+i] = udg[u - i + n] = false;
                    q[u][i] = '.';
                }
            }
        }
    }
    public static void main(String[]args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        for(int i = 0;i < n;i++) {
            Arrays.fill(q[i],'.');
        }
        dfs(0);
    }
}

解法二：

一个格子一个格子枚举，每个格子对应两个分支，放或不放，同时记录当前放的皇后个数，如果枚举完最后一行，且放的皇后有n个的话，收获一个结果

public class Main{
    static final int N = 20;
    static char[][]g = new char[N][N];
    static boolean[]row = new boolean[N];
    static boolean[]col = new boolean[N];
    static boolean[]dg = new boolean[N];
    static boolean[]udg = new boolean[N];
    static int n;
    
    /**
     * @param x 第几行
     * @param y 第几列
     * @param s 当前放了几个皇后
     */
    static void dfs(int x,int y,int s) {
        if(y == n) {
            y = 0;
            x++;
        }
        if(x == n) {
            if(s == n) {
                for(int i = 0;i < n;i++) {
                    for(int j = 0;j < n;j++) System.out.print(g[i][j]);
                    System.out.println();
                }
                System.out.println();
            }
        }else {
            //不放皇后
            dfs(x,y + 1,s);
            
            //放皇后
            if(!row[x] && !col[y] && !dg[x + y] && !udg[n + x - y]) {
                g[x][y] = 'Q';
                row[x] = col[y] = dg[x + y] = udg[x - y + n] = true;
                dfs(x,y + 1,s + 1);
                row[x] = col[y] = dg[x + y] = udg[x - y + n] = false;
                g[x][y] = '.';
            }
        }
    }
    
    public static void main(String[]args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        for(int i = 0;i < n;i++) {
            Arrays.fill(g[i],'.');
        }
        dfs(0,0,0);
    }
}

树和图的存储

**重边：**两个点之间有两条边

树是无环连通图

无向图就是一种特殊的有向图

模版：

//图的存储邻接表
int[]h = new int[N];
int[]e = new int[N];
int[]w = new int[N];//如果带权重
int[]ne = new int[N];
int idx;

void add(int a,int b,int c) {
    e[idx] = b;
    ne[idx] = h[a];
    w[idx] = c;
    h[a] = idx++;
}

//图的存储邻接矩阵
int[][]g = new int[N][N];

//存储a指向b
void add(int a,int b) {
    g[a][b] = 1;
}

DFS遍历

可以算出来每个子树的大小

//使用邻接表存储树
public class Main{
    static final int N = 100010;//节点数量
    static final int M = N * 2;//n个节点的树最多有n - 1条边，因为是无向图，需要*2
    static int[]h = new int[N];//指向第i个节点的第一条边
    static int[]e = new int[M];//第idx条边的终点
    static int[]ne = new int[M];//表示与第idx条边同起点的另一条边
    static boolean[]st = new boolean[N];//某节点是否被访问过
    static int idx;
    
    //添加a指向b
    static void add(int a,int b){
        e[idx] = b;
        ne[idx] = h[a];
        h[a] = idx++;
    }
    
    //dfs遍历
    static void dfs(int u) {
        st[u] = true;
        for(int i = h[u];i != -1;i = ne[i]) {
            int j = e[i];
            if(!st[j]) dfs(j);
        }
    }
    
    public static void main(String[]args) {
        Arrays.fill(h,-1);
    }
}

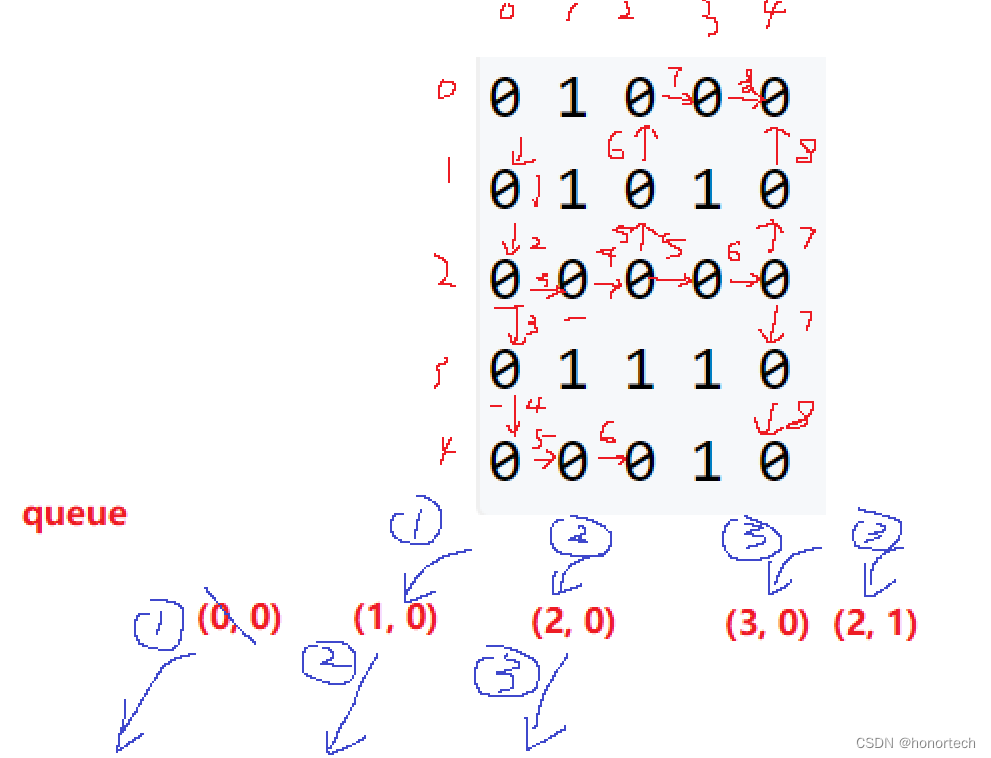
BFS遍历

while queue 不为空   {
	poll 队头t
	拓展 t 的所有邻点 x 
		if  x 未被遍历
			x offer进队列
			d【x】= d【t】+ 1;
}

public class Main{
    static final int N = 100010;
    static int[]h = new int[N];
    static int[]e = new int[N];
    static int[]ne = new int[N];
    static int idx;
    static int n;
    
    static int[]d = new int[N];//1号点到n号点的距离
    static int[]q = new int[N];
    public static void main(String[]args) {
        Arrays.fill(h,-1);
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        int m = sc.nextInt();
        for(int i = 0;i < m;i++) {
            int a = sc.nextInt();
            int b = sc.nextInt();
            add(a,b);
        }
        System.out.println(bfs());
    }
    public static int bfs() {
        Arrays.fill(d,-1);
        int hh = 0;
        int tt = -1;
        q[++tt] = 1;
        d[1] = 0;
        while(hh <= tt) {
            int t = q[hh++];
            for(int i = h[t];i != -1;i = ne[i]) {
                int j = e[i];
                if(d[j] == -1) {
                    d[j] = d[t] + 1;
                    q[++tt] = j;
                }
            }
        }
        return d[n];
    }
    public static void add(int a,int b) {
        e[idx] = b;
        ne[idx] = h[a];
        h[a] = idx++;
    }
}

应用

拓扑排序

一定是针对有向图的

定义：

对于一个序列，对应图上每条边都是起点在终点前面

易知，如果存在环的话，就一定不存在拓扑序列

所以，有向无环图又被称为拓扑图

入度为0的点可以作为起点，所以，拓扑排序步骤如下：
把所有入度为0的点入队
//类似与bfs过程
while queue不空 {
    t = poll队头;
    枚举所有t的出边 t -> j
        删掉 t -> j;
    	d[j]--;//j的入度减一
    	if(d[j] == 0) 将j入队
}
如果一个图没有环，我们一定可以找到入度为0的点，就可以写出拓扑序列

例如：

import java.util.*;
public class Main{
    static final int N = 100010;
    static int[]h = new int[N];
    static int[]e = new int[N];
    static int[]ne = new int[N];
    static int idx;
    static int n;
    static int[]q = new int[N];
    static int[]d = new int[N];//存入度
    public static void add(int a,int b) {
        e[idx] = b;
        ne[idx] = h[a];
        h[a] = idx++;
        d[b]++;
    }
    public static boolean topSort() {
        int hh = 0;
        int tt = -1;
        for(int i = 1;i <= n;i++) {
            if(d[i] == 0) q[++tt] = i;
        }
        while(tt >= hh) {
            int p = q[hh++];
            for(int i = h[p];i != -1;i = ne[i]) {
                int j = e[i];
                d[j]--;
                if(d[j] == 0) q[++tt] = j;
            }
        }
        return tt == n - 1;//如果全部元素如果都入过队，说明图中没有环
    }
    
    public static void main(String[]args) {
        Arrays.fill(h,-1);
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        int m = sc.nextInt();
        for(int i = 0;i < m;i++) {
            int x = sc.nextInt();
            int y = sc.nextInt();
            add(x,y);
        }
        if(topSort()) {
           for(int i = 0;i < n;i++) {
               System.out.print(q[i]+" ");
           }
        }else System.out.println("-1");
    }
}