机器学习-聚类算法详解

本文介绍: 与分类、回归任务不同，聚类任务事先并不知道任何样本标签，通过数据之间的内在关系把样本划分为若干类别，使得同类别之间的相似度高，不同类别之间的样本相似度低。K-means算法的基本思想是，通过迭代寻找K个簇（Clusterd）的一种划分方案，使得聚类结果对应的损失函数最小。K-means的核心目标是将数据集划分为K个簇，并给出的每个簇的中心点。其中Xi代表第i个样本，Ci是Xi所属的簇，U代表簇对应的中心点，M是样本的总数。

K-maens & DBSCAN
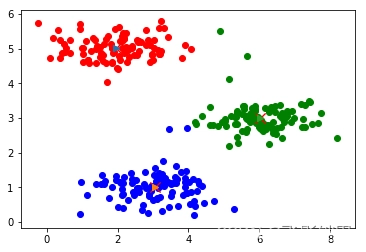
与分类、回归任务不同，聚类任务事先并不知道任何样本标签，通过数据之间的内在关系把样本划分为若干类别，使得同类别之间的相似度高，不同类别之间的样本相似度低。
K-means
基本思想
K-means算法的基本思想是，通过迭代寻找K个簇（Clusterd）的一种划分方案，使得聚类结果对应的损失函数最小。
其中，损失函数可以定义为各个样本距离所属簇中心点的误差平方和：

(

)

∑

∣

−

∣

J(c,mu) = sum_{i=1}^M|| x_i -mu_{c_i} || ^2

$J (c, μ) = i = 1 \sum M ∣∣ x_{i} - μ_{c_{i}} ∣ ∣^{2}$
其中Xi代表第i个样本，Ci是Xi所属的簇，U代表簇对应的中心点，M是样本的总数
具体步骤
K-means的核心目标是将数据集划分为K个簇，并给出的每个簇的中心点。具体步骤分为四步：

数据预处理。主要将数据标准化、异常点过滤
随机选取K个中心点
$mu_1^{(0)},mu_2^{(0)},…,mu_k^{(0)} μ1(0),μ2(0),…,μk(0)$
定义损失函数
$sum_{i=1}^M|| x_i -mu_{c_i} || ^2 J(c,μ)=i=1∑M∣∣xi−μci∣∣2$
令t=0，1，2。。。为迭代步数，重复以下步骤直到损失函数收敛：
- 对于每一个样本xi，将其分配到距离最近的中心
  $c_i^t <- argmin_k|| x_i – mu_k^t||^2 cit<−argmink∣∣xi−μkt∣∣2$
- 对于每一个类中心k，重新计算该类的中心
  $mu_k^{t+1} <- argmin_{mu} sum_{i:c^t_i=k}^b|| x_i – mu||^2 μkt+1<−argminμi:cit=k∑b∣∣xi−μ∣∣2 DBSCAN$

寻找核心点形成临时聚类簇。
扫描全部样本点，如果某个样本点R半径范围内点数目>=MinPoints，则将其纳入核心点列表，并将其密度直达的点形成对应的临时聚类簇。
合并临时聚类簇得到聚类簇。
对于每一个临时聚类簇，检查其中的点是否为核心点，如果是，将该点对应的临时聚类簇和当前临时聚类簇合并，得到新的临时聚类簇。
重复此操作，直到当前临时聚类簇中的每一个点要么不在核心点列表，要么其密度直达的点都已经在该临时聚类簇，该临时聚类簇升级成为聚类簇。
继续对剩余的临时聚类簇进行相同的合并操作，直到全部临时聚类簇被处理。
聚类算法的各自缺点：
K-means 问题：

第一个就是对簇的数量的选择，我们希望指定一个簇数K，以使每个点和其最近的簇的距离之和最小。但是在实际情况中，我们很难找到一个合适的K值，因为我们不知道应该将数据分为几类。
Kmeans 算法会把所有的数据点都进行分类，但是很多情况下，会有一些离群点，这些点应该被剔除的，但是 Kmeans 算法还是会把它们归为某一类。
k均值聚类假设对每个簇来说，所有的方向都同等重要。这也就意味着k均值聚类主要适用于球形分布的数据，对于其他分布的数据分类可能不好。
DBSCAN缺点：
如果样本集的密度不均匀、聚类间距差相差很大时，聚类质量较差，这时用DBSCAN聚类一般不适合。
如果样本集较大时，聚类收敛时间较长，此时可以对搜索最近邻时建立的KD树或者球树进行规模限制来改进。
调参相对于传统的K-Means之类的聚类算法稍复杂，主要需要对距离阈值ϵϵ，邻域样本数阈值MinPoints联合调参，不同的参数组合对最后的聚类效果有较大影响。
聚类算法的优点：
K-means：
高效可伸缩，计算复杂度接近于线性（N是数据量，K是聚类总数，t是迭代轮数）。
收敛速度快，原理相对通俗易懂，可解释性强。
BDSCAN：
可以对任意形状的稠密数据集进行聚类，相对的，K-Means之类的聚类算法一般只适用于凸数据集。
可以在聚类的同时发现异常点，对数据集中的异常点不敏感。
聚类结果没有偏倚，相对的，K-Means之类的聚类算法初始值对聚类结果有很大影响