【代码随想录】刷题笔记Day47

本文介绍: 动规8：打家劫舍I/II/III

前言

又过了个愉快的周末~大组会终于不用开了，理论上已经可以回家了！但是我多留学校几天吧，回家实在太无聊了，也没太多学习的氛围

198. 打家劫舍 – 力扣（LeetCode）

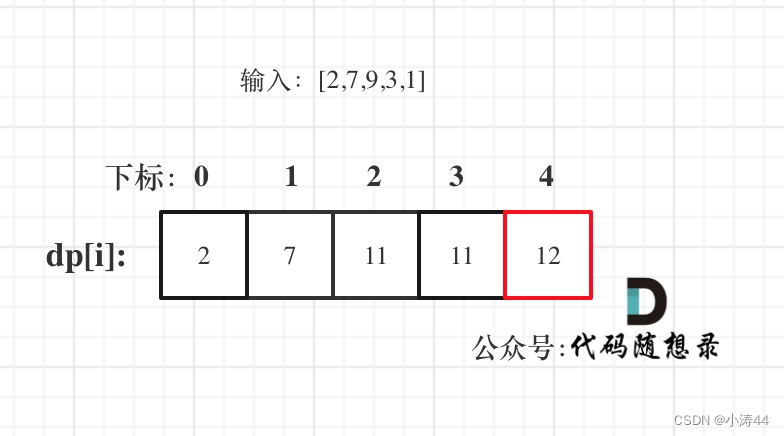
dp[i]含义
- 考虑下标i（包括i）以内的房屋，最多可以偷窃的金额为dp[i]
递推公式：包含偷和不偷
- dp[i] = max(dp[i – 2] + nums[i], dp[i – 1]);
初始化
- dp[0] = nums[0]，dp[1] = max(nums[0], nums[1]);
遍历顺序：类似斐波那契，从前往后推导

class Solution {
public:
    int rob(vector<int>& nums) {  
        if(nums.size() == 1) return nums[0];
        vector<int> dp(nums.size());
        dp[0] = nums[0];
        dp[1] = max(nums[0], nums[1]);
        for(int i = 2; i < nums.size(); i++){
            dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
        }
        return dp[nums.size() - 1];
    }
};

213. 打家劫舍 II – 力扣（LeetCode）

本题难点在于将环形问题拆解成线性问题，分为三种情况
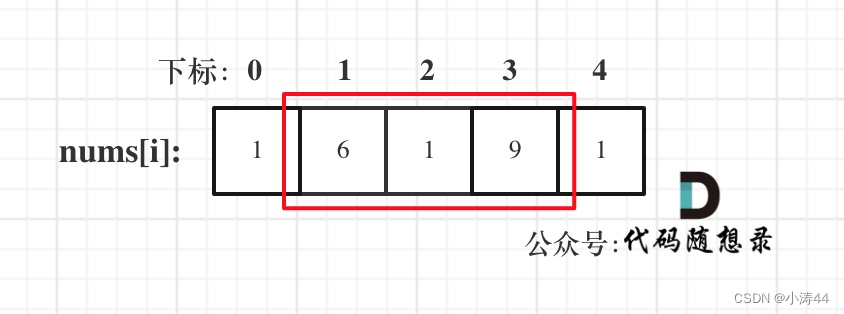
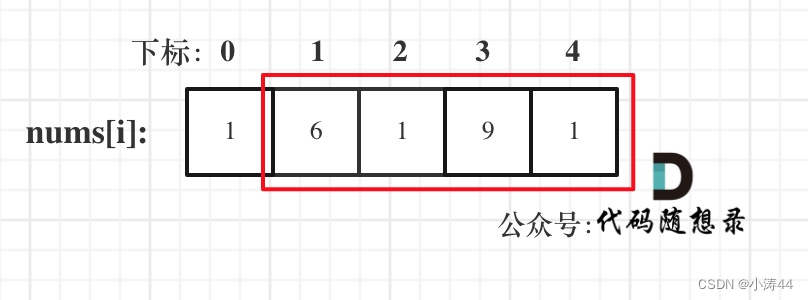
情况一：考虑不包含首尾元素
情况二：考虑包含首元素，不包含尾元素
情况三：考虑包含尾元素，不包含首元素
情况二、三是包含情况一的，所以把掐头去尾的数组传到上一题取最大值便可

// 方法一：传掐头去尾的数组
class Solution {
public:
    int rob(vector<int>& nums) {
        if (nums.size() == 0) return 0;
        if (nums.size() == 1) return nums[0];
        int result1 = robRange(nums, 0, nums.size() - 2); // 情况二
        int result2 = robRange(nums, 1, nums.size() - 1); // 情况三
        return max(result1, result2);
    }
    // 198.打家劫舍的逻辑
    int robRange(vector<int>& nums, int start, int end) {
        if (end == start) return nums[start];
        vector<int> dp(nums.size());
        dp[start] = nums[start];
        dp[start + 1] = max(nums[start], nums[start + 1]);
        for (int i = start + 2; i <= end; i++) {
            dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
        }
        return dp[end];
    }
};

还有一个很妙的方法，遍历一次，同时更新两个dp数组（掐头 + 去尾）

class Solution {
public:
    int rob(vector<int>& nums) {
        int n = nums.size();
        if(n == 1) return nums[0];
        vector<int> dp1(n), dp2(n);
        // 掐头，考虑1 ~ n-1，取n-1
        dp1[0] = 0;         
        dp1[1] = nums[1];
        // 去尾，考虑0 ~ n-2，取n-2
        dp2[0] = nums[0];
        dp2[1] = max(nums[0], nums[1]);
        for(int i = 2; i <= n - 1; i++){
            dp1[i] = max(dp1[i - 2] + nums[i], dp1[i - 1]);
            if(i <= n - 2){
                dp2[i] = max(dp2[i - 2] + nums[i], dp2[i - 1]);
            }
        }
        return max(dp1[n - 1], dp2[n - 2]);
    }
};

337. 打家劫舍 III – 力扣（LeetCode）

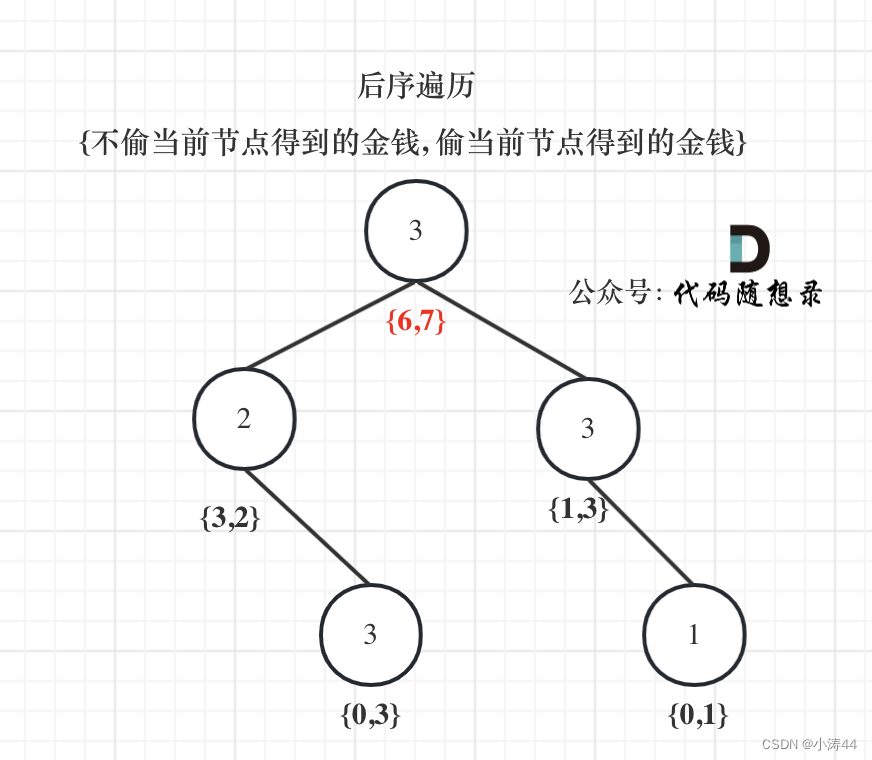
树形dp入门题目，记录每个节点偷和不偷的状态，递归后序遍历将最优解集中到根节点上
dp数组是一个长度为2的数组，在递归的过程中，系统栈会保存每一层递归的参数

class Solution {
public:
    int rob(TreeNode* root) {
        vector<int> result = robTree(root);
        return max(result[0], result[1]);
    }
    // 长度为2的数组，0：不偷，1：偷
    vector<int> robTree(TreeNode* root){
        if(root == nullptr) return {0, 0};
        vector<int> left = robTree(root->left);
        vector<int> right = robTree(root->right);
        // 不偷cur，那么可以偷也可以不偷左右节点，则取较大的情况
        int val0 = max(left[0], left[1]) + max(right[0], right[1]);
        // 偷cur，那么就不能偷左右节点。
        int val1 = root->val + left[0] + right[0];
        return {val0, val1};
    }
};