刷题的第二十九天,希望自己能够不断坚持下去,迎来蜕变。😀😀😀
刷题语言:C++
Day29 任务
● 01背包问题,你该了解这些!
● 01背包问题,你该了解这些! 滚动数组
● 416. 分割等和子集
1 动态规划:01背包问题,你该了解这些!

背包问题的理论基础重中之重是01背包
1.1 01 背包
01 背包:有n件物品和一个最多能背重量为w的背包。第i件物品的重量是weight[i],得到的价值是value[i]。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大

| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
二维dp数组01背包
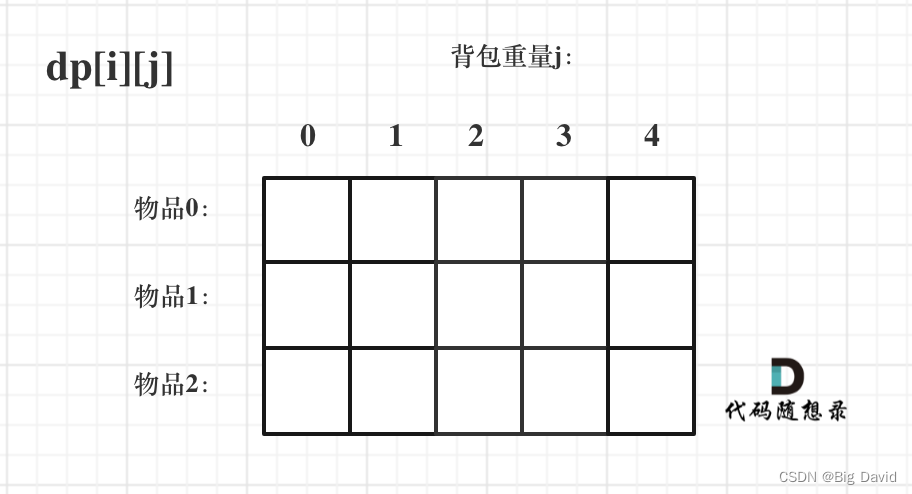
(1)确定dp数组以及下标的含义
dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
(2)确定递推公式
1.不放物品i:由dp[i – 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i – 1][j]。(其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以背包内的价值依然和前面相同。)
2.放物品i:由dp[i – 1][j – weight[i]]推出,dp[i – 1][j – weight[i]] 为背包容量为j – weight[i]的时候不放物品i的最大价值,那么dp[i – 1][j – weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
(3)dp数组如何初始化
首先从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。如图:
状态转移方程是由 i-1 推导出来,那么i为0的时候就一定要初始化
dp[0][j],即:i为0,存放编号0的物品的时候,各个容量的背包所能存放的最大价值。
那么很明显当 j < weight[0]的时候,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小。
当j >= weight[0]时,dp[0][j] 应该是value[0],因为背包容量放足够放编号0物品
for (int j = 0; j < weight[0]; j++) {
dp[0][j] = 0;
}
for (int j = weight[0]; j <= bagweight; j++) {
dp[0][j] = value[0];
}
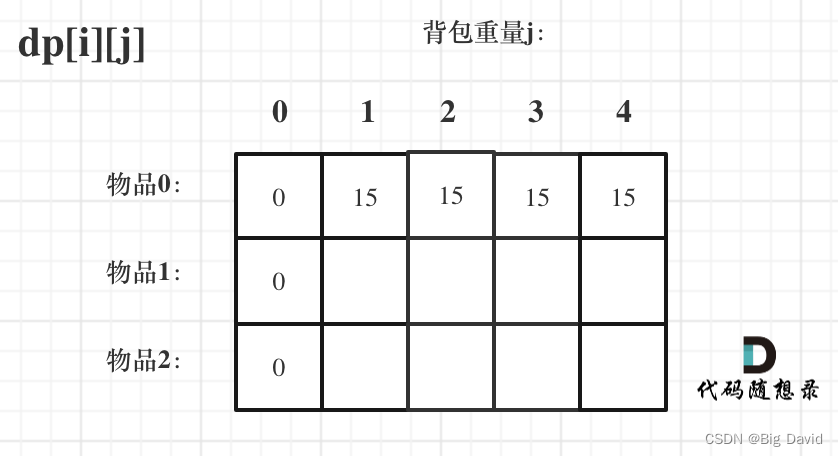
dp[0][j] 和 dp[i][0] 都已经初始化,其他下标的初始化什么数值都可以,因为都会被覆盖。
vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
for (int j = weight[0]; j <= bagweight; j++) {
dp[0][j] = value[0];
}
(4)遍历顺序
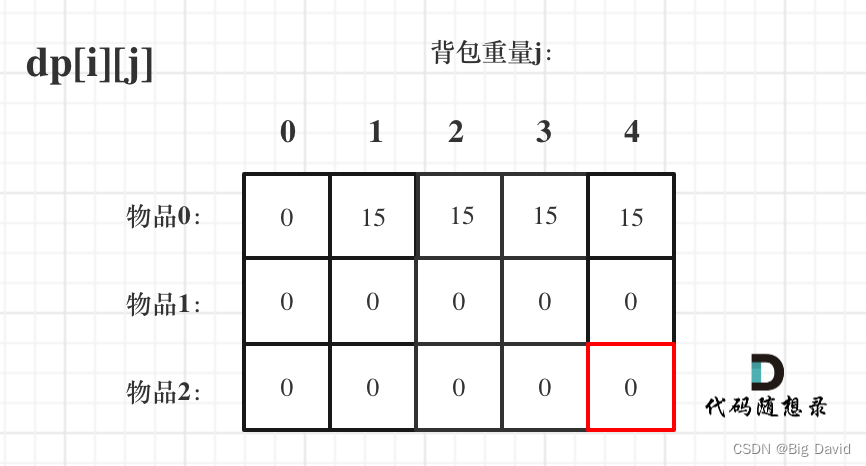
先遍历物品,然后遍历背包重量
for (int i = 1; i < weight.size(); i++) {
for (int j = 0; j <= bagweight; j++) {
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
先遍历背包,再遍历物品
// weight数组的大小 就是物品个数
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
for(int i = 1; i < weight.size(); i++) { // 遍历物品
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
(5)举例推导dp数组
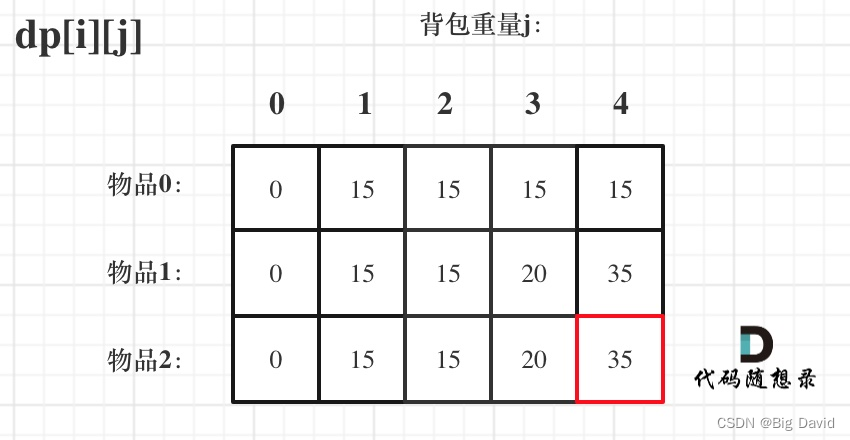
C++:
void test_2_wei_bag_problem1() {
vector<int> weight = {1, 3, 4};
vector<int> value = {15, 20, 30};
int bagweight = 4;
// 二维数组
vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
// 初始化
for (int j = weight[0]; j <= bagweight; j++) {
dp[0][j] = value[0];
}
for (int i = 1; i < weight.size(); i++) {
for (int j = 0; j <= bagweight; j++) {
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
cout << dp[weight.size() - 1][bagweight] << endl;
}
int main() {
test_2_wei_bag_problem1();
}
2 动态规划:01背包理论基础(滚动数组)
背包最大重量为4。
物品为:
| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
一维dp数组:上一层可以重复利用,直接拷贝到当前层。
dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
(1)确定dp数组的定义
dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]
(2)一维dp数组的递推公式
dp[j]有两个选择,一个是取自己dp[j] 相当于 二维dp数组中的dp[i-1][j],即不放物品i,一个是取dp[j – weight[i]] + value[i],即放物品i,指定是取最大的,毕竟是求最大价值
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
(3)一维dp数组如何初始化
假设物品价值都是大于0的,所以dp数组初始化的时候,都初始为0
(4)一维dp数组遍历顺序
for (int i = 0; i < weight.size(); i++) {// 遍历物品
for (int j = bagweight; j >= weight[i]; j--) {// 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
倒序遍历是为了保证物品i只被放入一次! 如果一旦正序遍历了,那么物品0就会被重复加入多次!
为什么二维dp数组遍历的时候不用倒序呢?
因为对于二维dp,dp[i][j]都是通过上一层即dp[i – 1][j]计算而来,本层的dp[i][j]并不会被覆盖!
(5)举例推导dp数组
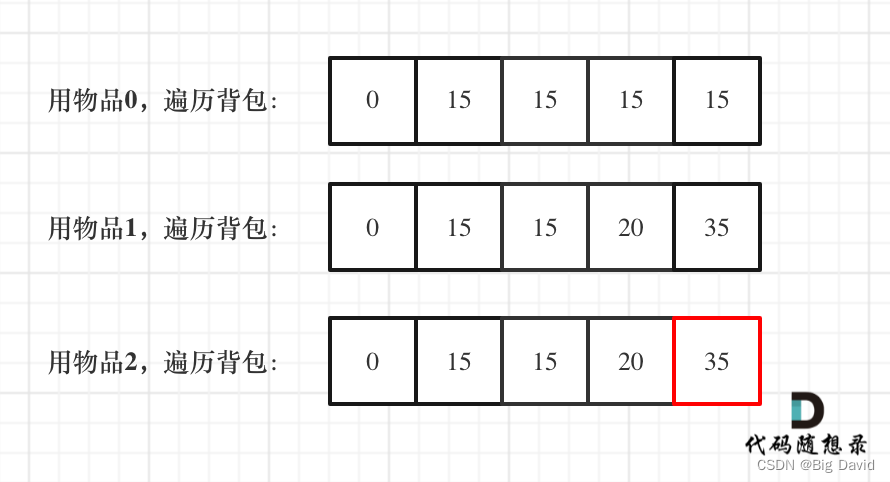
C++:
void test_1_wei_bag_problem() {
vector<int> weight = {1, 3, 4};
vector<int> value = {15, 20, 30};
int bagWeight = 4;
// 初始化
vector<int> dp(bagWeight + 1, 0);
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
cout << dp[bagWeight] << endl;
}
int main() {
test_1_wei_bag_problem();
}
3 分割等和子集
416. 分割等和子集

思路:
背包问题,有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
本题使用的是01背包,因为元素我们只能用一次。
把01背包问题套到本题:
(1)背包的体积为sum / 2
(2)背包要放入的商品(集合里的元素)重量为 元素的数值,价值也为元素的数值
(3)背包如果正好装满,说明找到了总和为 sum / 2 的子集。
(4)背包中每一个元素是不可重复放入。
动态规划
(1)确定dp数组以及下标的含义
01背包中,dp[j] 表示: 容量为j的背包,所背的物品价值最大可以为dp[j]
本题:dp[j]表示 背包总容量(所能装的总重量)是j,放进物品后,背的最大重量为dp[j]
(2)确定递推公式
01背包的递推公式为:dp[j] = max(dp[j], dp[j – weight[i]] + value[i]);
本题,相当于背包里放入数值,那么物品i的重量是nums[i],其价值也是nums[i]。
所以递推公式:dp[j] = max(dp[j], dp[j – nums[i]] + nums[i]);
(3)dp数组如何初始化
dp[0]一定是0。
如果题目给的价值都是正整数那么非0下标都初始化为0就可以了,如果题目给的价值有负数,那么非0下标就要初始化为负无穷。
这样才能让dp数组在递推的过程中取得最大的价值,而不是被初始值覆盖了
(4)确定遍历顺序
for (int i = 0; i < nums.size(); i++) {
for (int j = target; j >= nums[i]; j--) {// 每一个元素一定是不可重复放入,所以从大到小遍历
dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
}
}
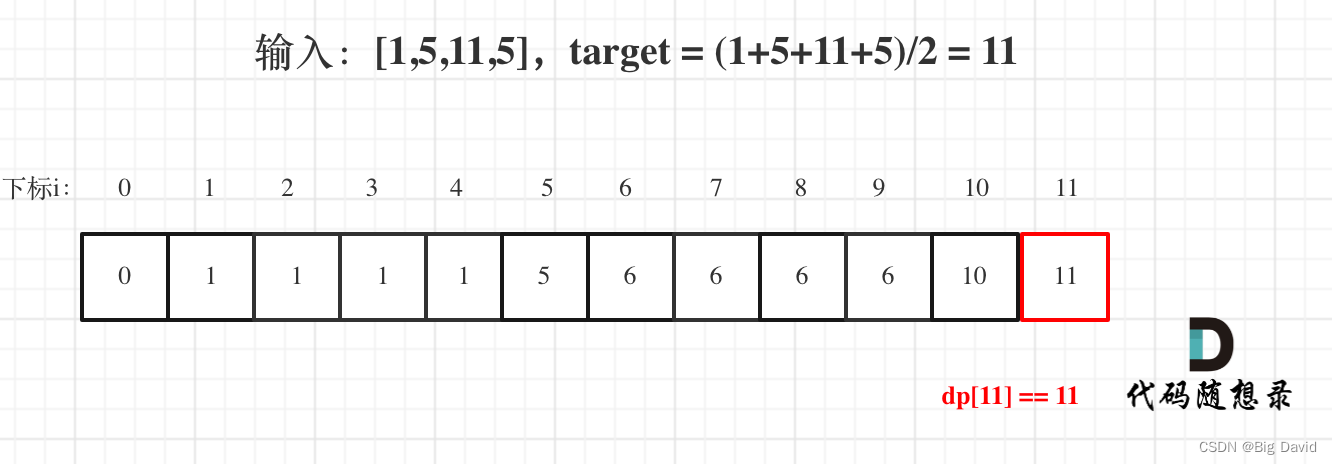
(5)举例推导dp数组
dp[j]的数值一定是小于等于j的,如果dp[j] == j 说明,集合中的子集总和正好可以凑成总和j
C++:
class Solution {
public:
bool canPartition(vector<int>& nums) {
int sum = 0;
vector<int> dp(10001, 0);
for (int i = 0; i < nums.size(); i++) {
sum += nums[i];
}
if (sum % 2 == 1) return false;
int target = sum / 2;
// 开始 01背包
for(int i = 0; i < nums.size(); i++) {
for(int j = target; j >= nums[i]; j--) { // 每一个元素一定是不可重复放入,所以从大到小遍历
dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
}
}
// 集合中的元素正好可以凑成总和target
if (dp[target] == target) return true;
return false;
}
};
时间复杂度:
O
(
n
2
)
O(n^2)
O(n2)
空间复杂度:
O
(
n
)
O(n)
O(n),虽然dp数组大小为一个常数,但是大常数
鼓励坚持三十天的自己😀😀😀
原文地址:https://blog.csdn.net/BigDavid123/article/details/135471922
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_54428.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!