本文介绍: 在这个例子中,贪心思想体现在按照区间的起始值进行排序,并在遍历过程中合并重叠的区间。通过一次排序和一次线性遍历,我们就能够完成区间的合并,而不需要复杂的数据结构或算法。具体来说,通过将区间按照起始值升序排序,我们确保了在遍历时,当前区间与之前已合并的区间有序。如果有重叠,则检查当前区间的结束值是否大于上一个合并区间的结束值。如果当前区间与上一个合并区间没有重叠,将其添加到列表中。一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间。将当前区间的起始值与上一个合并区间的结束值(空间复杂度:O(logn)
题目(难度中等)
示例
示例 1:
示例 2:
思想
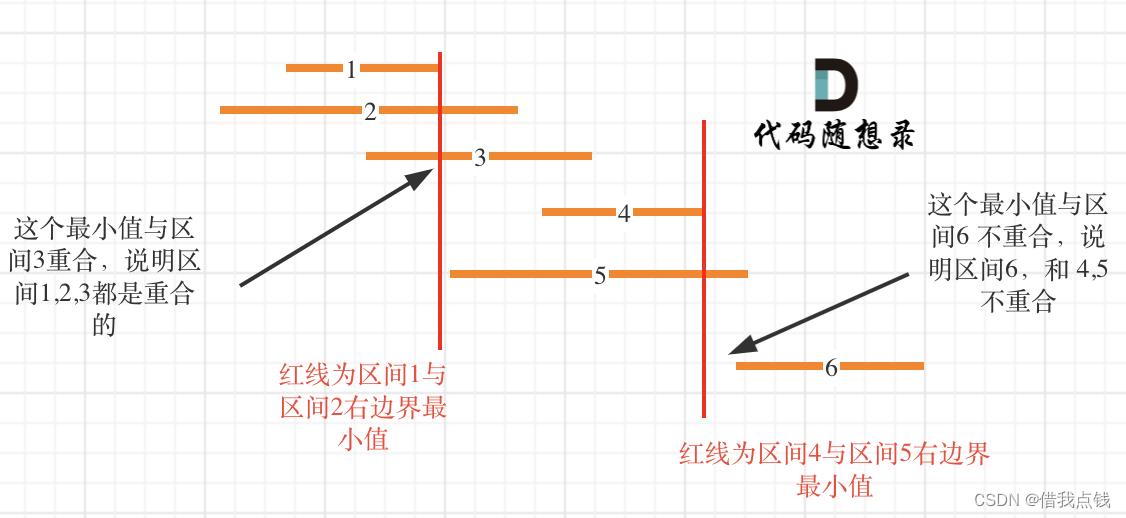
区间合并的贪心思想。贪心算法的基本思想是每一步都选择当前状态下最优的解,而不考虑全局最优解。在这个例子中,贪心思想体现在按照区间的起始值进行排序,并在遍历过程中合并重叠的区间。
具体来说,通过将区间按照起始值升序排序,我们确保了在遍历时,当前区间与之前已合并的区间有序。然后,通过比较当前区间的起始值和上一个合并区间的结束值,我们可以确定是否需要合并这两个区间。
这种贪心策略的优势在于它的简单性和高效性。通过一次排序和一次线性遍历,我们就能够完成区间的合并,而不需要复杂的数据结构或算法。当然,这种方法前提是输入的区间是无重叠的。
算法分析与设计
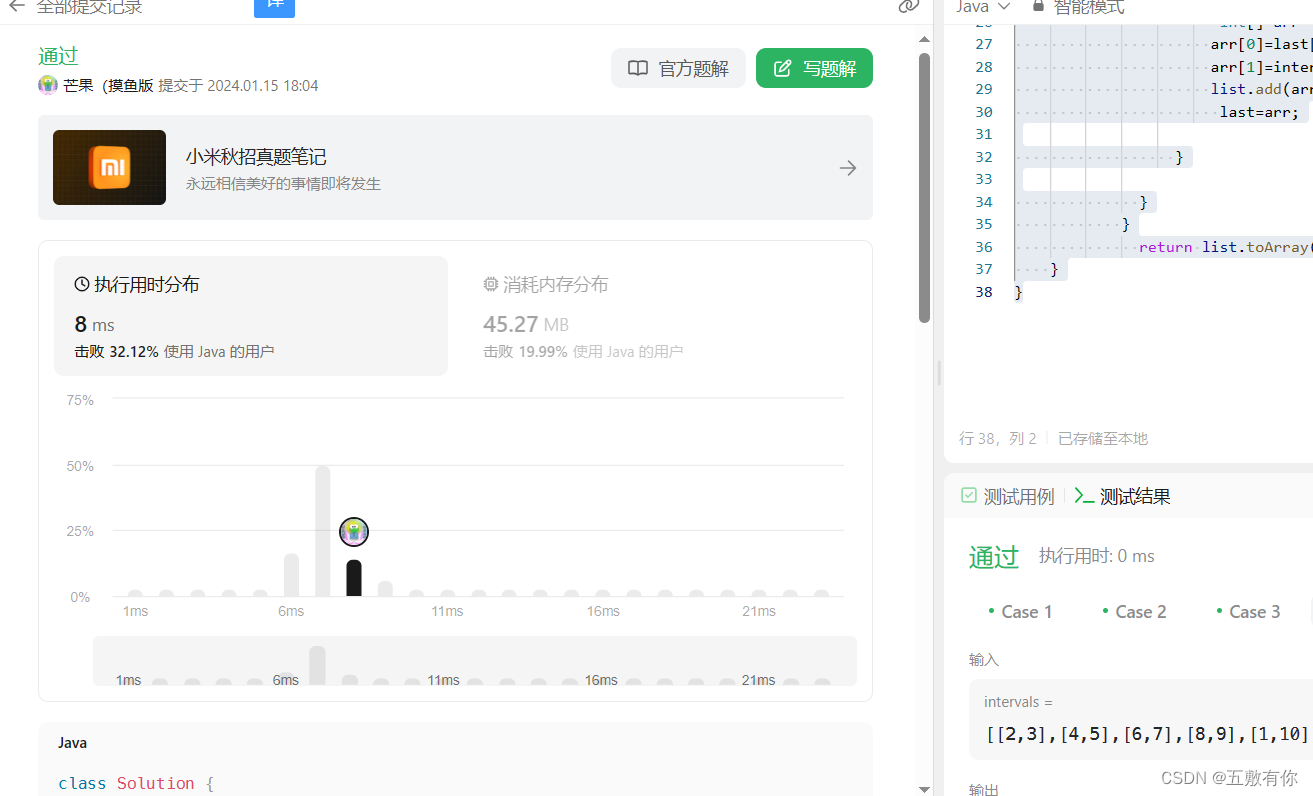
代码实现
运行结果
时间复杂度:O(nlogn)
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。