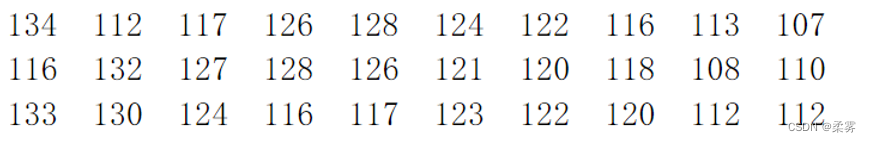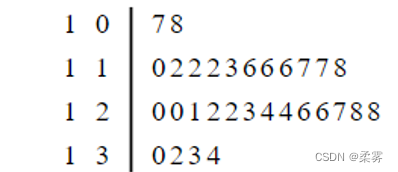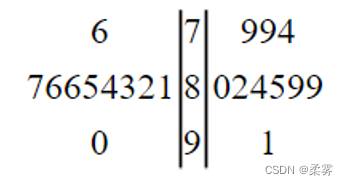本文介绍: 本篇介绍的是数值型数据怎么进行数据可视化,本篇介绍的有直方图、茎叶图、箱线图。
前言
本篇介绍的是数值型数据怎么进行数据可视化,本篇介绍的有直方图、茎叶图、箱线图。
直方图
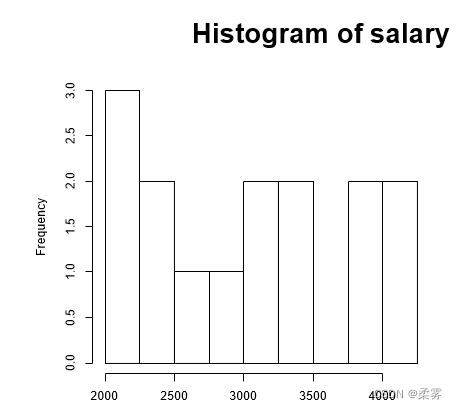
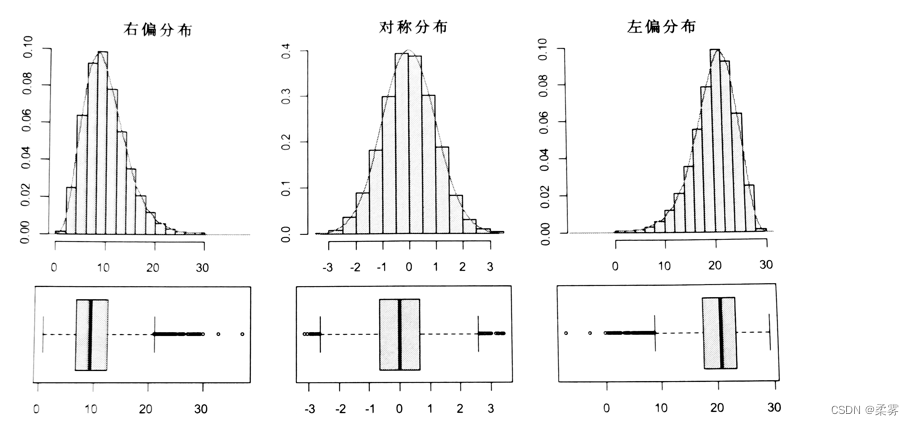
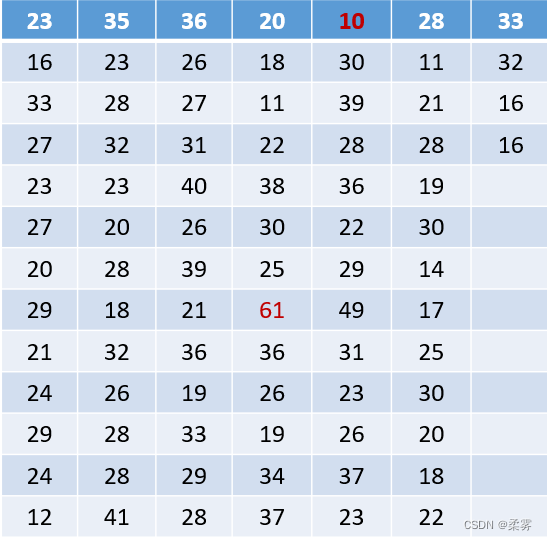
直方图(Histogram)用于描述连续型变量的频数分布,实际应用中常用于考察变量的分布是否对称;是否服从某种分布类型,如正态分布
直方图以矩形的面积表示各组段的频数或频率, 各矩形的面积总和为总频数(或等于1,此时是按照频率来计算的)
在R软件里用函数是hist()来作直方图,把probability参数设置为T是用频率作直方图,默认为F。
示例如下:
代码:
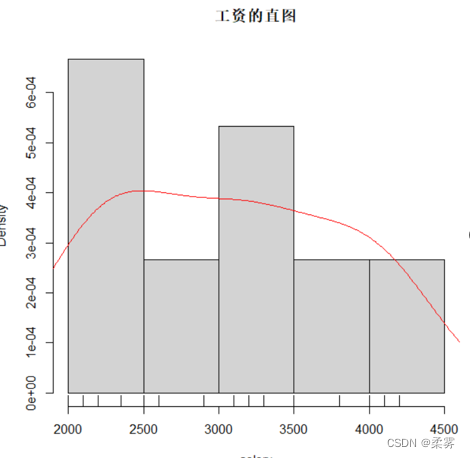
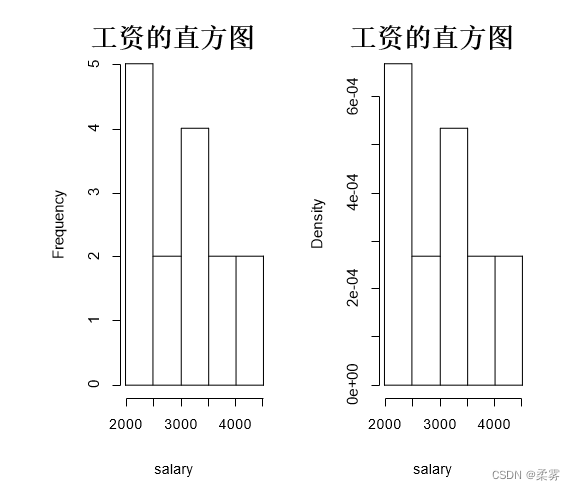
继续对工资数据作直方图,结果如下图。
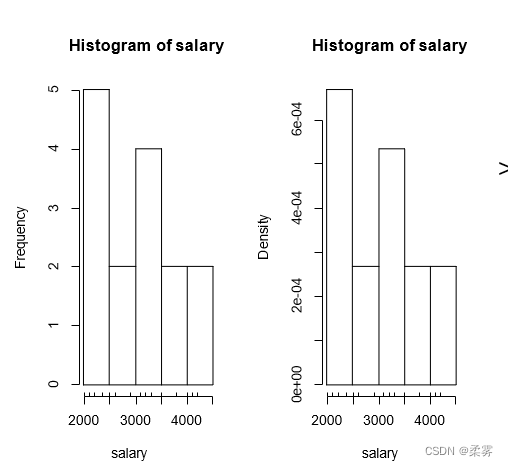
在R里还可以使用rug()函数把各个数据竖线(轴须线)描绘在X轴上,结果如下所示:
在R里还可以使用lines(density(x))函数增加核密度估计曲线(plot(density(x))),结果如下图所示:
茎叶图
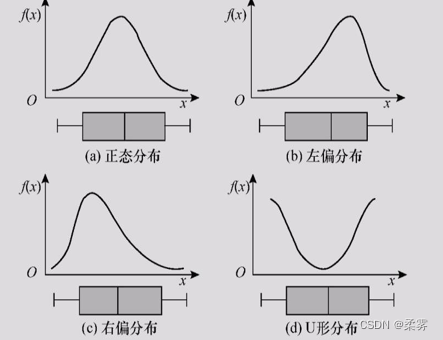
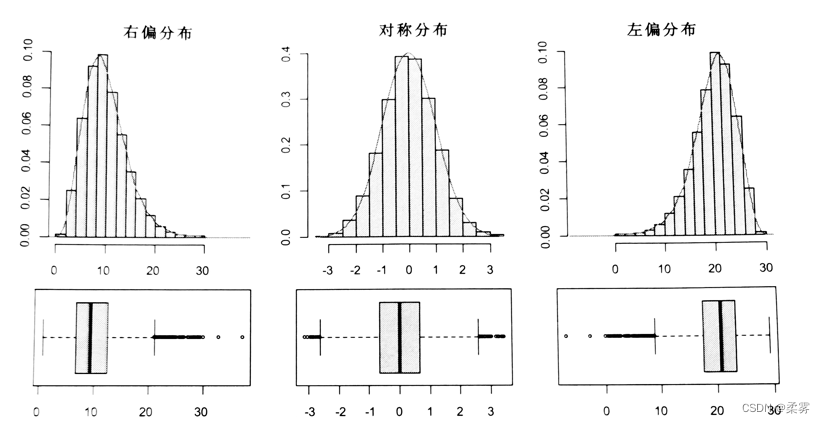
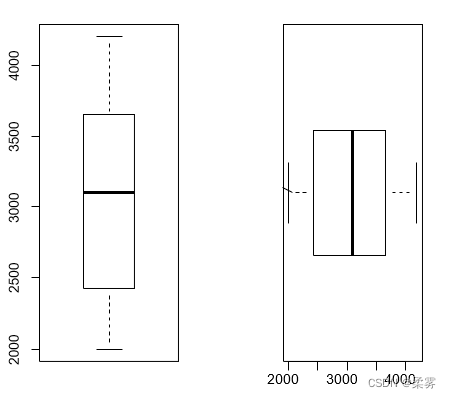
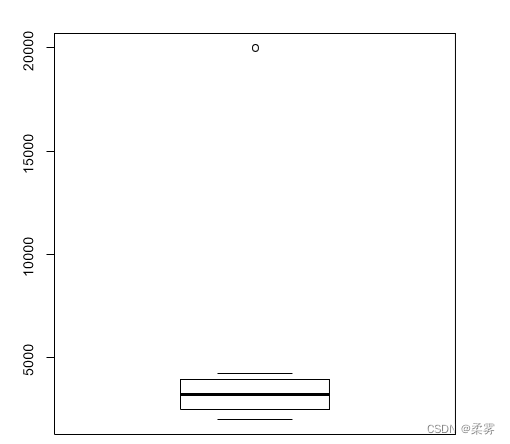
箱线图
练习
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。