统计学-R语言-4.2

前言

本篇介绍下数据的描述性分析。

单变量数据的描述分析

分类型数据

统计学上把取值范围是有限个值或是一个数列构成的变量称为离散型变量，其中表示分类情况的离散型变量又称为分类变量。
对于分类数据，可以用频数表来分析，也可以用条形图和饼图来描述。

频数表

频数表(frequency table)或频数分布表(frequency distribution table)可以描述分类变量的分布概况。
频数表是遵循既不重叠又不遗漏的原则，按变量 (数据特征)的取值归类分组，把总体的所有数据按组归并排列，由各个组别所包含的数据频数构成的汇总表格。
R中的函数table()可以生成频数表。如果x是分类数据，只要用table(x)就可以生成分类频数表。

频数表的特殊情况：
频数表用来描述分类变量的分布概况。
但是，对于一些数值型数据，可以将数值型数据进行，诸如像：“划分区间”、“分类”等一些处理，将数值型数据转化为分类型数据进行分析。此时可以使用频数表来描述数据的分布情况。

例题1：
下表是某蓝球运动员2008-2009赛季常规赛的每场得分数据，下面我们一起来分析这组数据。

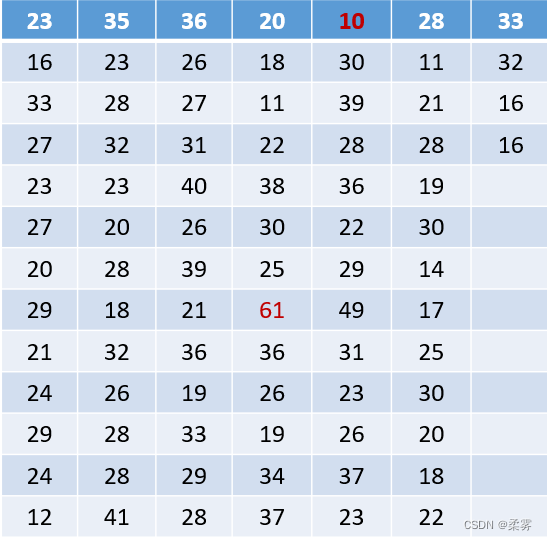
通过观察，我们可以找出最大值为61，最小值为10。再将最小值到最大值之间划分为6个区间，分别是10_20、2130、31_40、4150、51_60、6170，统计有多少个数据落在这6个区间内，并记录下来，便得到了如下表所示的频数分布表。

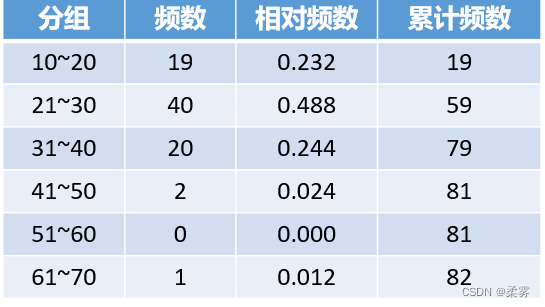
表中的第一列是分组方式；第二列是频数，即每个区间里有多少个数据；第三列是相对频数，即频数除以数据总量；第四列是累积频数，即对频数进行累积计数。
这张表格包含了数据分析的三个重要的思路：
一是分类统计，体现在频数中，即把数据按照某种属性进行分类计数；
二是相对数量，体现在相对频数中，相对频数的本质是将频数进行“归一化”，这样便于与其他数据进行对比；
这张表格包含了数据分析的三个重要的思路：
三是累积数量统计，体现在累积频数中，对数量进行累积统计便于我们观察出数量的变化规律，也便于我们快速找出低于或高于某些临界值的数据有多少，比如，从累积频数一列中，我们可以知道，低于30分的有59场，低于40分的有79场。

例题2：
(数据：example2_1.RData)某物业管理公司准备进行一项物业管理的改革措施，为征求社区居民的意见，在所管理的4个社区随机调查 80个住户，对户主进行调查。表中数据记录的是被调查者所在的社区、被调查者的性别及其对该项改革措施的态度数据。
生成简单频数分布表，观察被调查者所在的社区、性别以及对改革措施态度的分布状况

load("C:/Users/125/Desktop/example/ch2/example2_1.RData")
example2_1

使用summary函数生成频数分布表

summary(example2_1)

生成被调查者所在社区的频数分布表，并将频数分布表转化成百分比

count1<-table(example2_1$社区);count1#生成被调查者所在社区的频数分布表
prop.table(count1)*100#将频数分布表转化成百分比

生成被调查者性别的频数分布表，并将频数表转化成百分比

count2<-table(example2_1$性别);count2
prop.table(count2)*100

生成被调查者态度的频数分布表，并将频数表转化成百分比

count3<-table(example2_1$态度);count3
prop.table(count3)*100 

条形图

条形图(barchart,barplot,bargraph)是用等宽直条的长短来表示各个相互独立的指标数值大小的图形，可以描述已经用频数或频率汇总了的定性变量，还可以描述离散定量变量数据的频数、频率或概率分布。
条形图适用于相互独立的数据(数据明确分组，不连续)
坐标横轴代表定性变量的各个取值，在每个变量位置的条的长度和其所代表的水平的频数或频率成比例
条形图中每一个条形都代表一个分组
条形图的高度可以是频数或频率
纵轴和横轴可以互换
条形图分为单式和复式两种，单式适用于只有一组观察数据，复式适用于有若干组观察数据。
条形图有很多变种：横纵可以互换，这决定了条形是垂直放置（柱形图）还是水平放置。

R画条形图的函数是barplot()，对分类数据作条形图需先对原始数据分组，否则作出的图将不是分类数据的条形图（当数据量大的时候，可以用以描绘数据的分布形状）。

示例如下：
当有两个类别变量时，可以绘制成复式条形图。根据绘制方式不同，复式条形图有并列条形图（juxtaposed bar plot）和堆叠条形图（stacked bar plot）等。以例2-3的数据为例，绘制复式条形图的R代码如下所示：

load("C:/example/ch2/example2_1.RData")
mytable1<-table(example2_1$态度,example2_1$社区)#制作出态度和社区的频数分布表
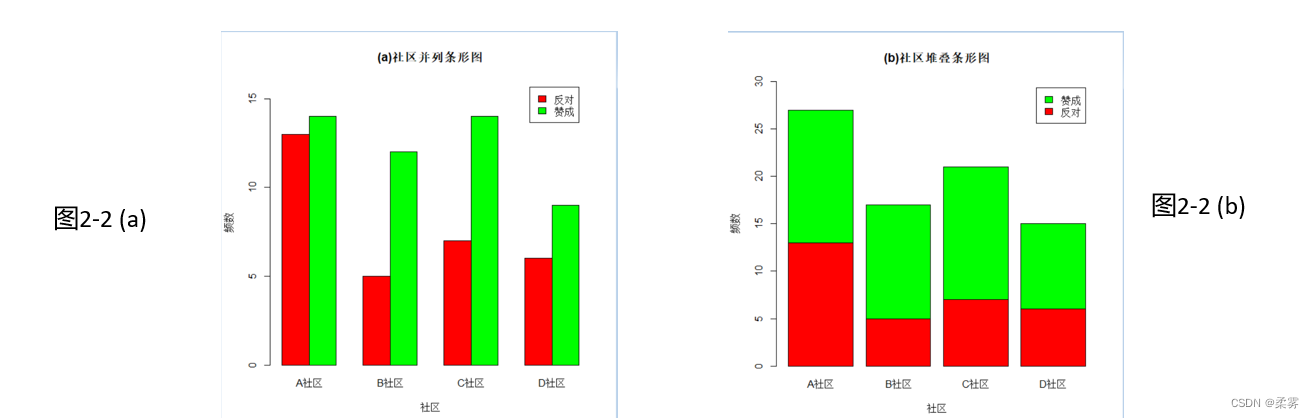
bar1<-barplot(mytable1,xlab="社区",ylab="频数",ylim=c(0,16),col=c("red","green"),legend=rownames(mytable1),args.legend=list(x=12),beside=TRUE,main="(a)社区并列条形图")#ylim=c()设定坐标轴取值范围，legend设置图例，args.legend设置图例的位置参数
bar2<-barplot(mytable1,xlab="社区",ylab="频数",ylim=c(0,30),col=c("red","green"),legend=rownames(mytable1),args.legend=list(x=4.8),main="(b)社区堆叠条形图")

图2-2（a）和图2-2（b）是两种不同形式的复式条形图，反映不同社区赞成和反对的人数分布。从中可以看出，B社区和C社区赞成的人数明显多于反对的人数，而A社区和D社区赞成和反对的人数差异不大。

饼图

饼图(pie chart)又叫圆形图,是一个面积为100%,由许多扇形组成的圆,各个扇形的大小比例等于变量各个水平(或类别)的频率或比例,即表示了不同组成部分的相对重要性。
饼图对描述定类尺度的数据特别有用。
饼图比条形图简单,描述比例较直观。与条形图一 样，对原始数据做饼图前要先分组。
在R软件中使用函数pie()就可以画饼图。

例题1：
假如对25个学生的籍贯进行调查，按照东部 (1)、中部(2)、西部(3)、东北部(4)分成四类。调查数据如下:3,4,1,1,3,4,3,3,1,3,2,1,2,1,2,3,2,3,1,1,1,1,4,3,4

x=c(3,4,1,1,3,4,3,3,1,3,2,1,2,1,2,3,2,3,1,1,1,1,4,3,4)
par(mfrow=c(1,2))
d=table(x)
pie(d)

names(d)=c ("东部","中部","西部","东北部") #用文字标识籍贯的分类
pie(d)

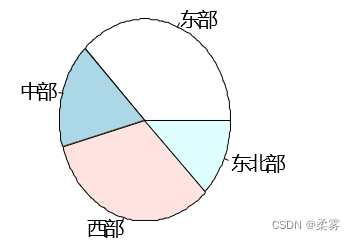
在R软件中通过参数设置还可以对饼图的各个扇区的颜色进行修改，如将颜色改成紫色、绿色、青色和白色。

pie(d,col=c("purple","green","cyan","white")

数值型数据

描述数据中心位置或集中趋势的度量方法：均值、中位数、众数、分位数
描述数据离散程度的度量方法：极差、样本标准差、变异系数
描述数据形状的统计量：偏度、峰度

数值型数据

对于数值型数据，每个数据都有自己的位置，有时候需要描述数据的“中间”或“中心”在哪里,数据离中心多远,或者数据中有多少数据点是小于某个数等。
用来描述中心位置或集中趋势的度量方法主要有均值、中位数和众数。

数据的集中趋势–均值

最常用的描述数据的中心位置(central location)或集中趋势 (center tendency)的度量方法就是均值(mean)
均值反映同类现象在特定条件下所达到的平均水平
如果观测数据为x1,x2,…,xn,那么样本均值定义为

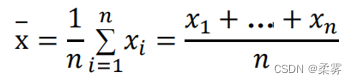
式中: n为数据集中的数据个数(样本量);xi为样体中的第i个数据
如，2015年我国的国内生产总值GDP为6767万亿元，我国同期的人口总数约为13亿，因此，人均GDP为5.2万元。

如果数据已经分组得到了频数分布，一些观测可能具有相同的数值，一个较为简便的计算均值的方法是计算加权平均数。
设数据x1,x2,…,xn相应的频数分别为w1,w2,…,wn，则加权平均数（weighted mean）的公式为：

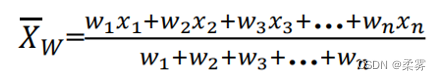
数据的集中趋势–众数

众数(mode)是另一种集中趋势度量方法。
众数就是数据中重复出现次数最多的数。
在样本的观测值没有重复的时候(这多出现在连续变量的情况),众数就没有意义。
在离散定量变量(包括四舍五入的连续变量)和定性变量情况,众数常常有意义,它能明确反映数据分布的集中趋势。特别在定性变量时,哪一类(水平)出现的频数最大,它就是众数。
分位数(α-quantile)也可以描述数据的相对位置，定义为约有α比例的样本点小于它，或者α%的样本点小于它
中位数就是50%分位数。
四分位数：
四分位数（quartile）是一组数据排序后处在25%和75%位置上的数值。它是用3个点将全部数据等分为四部分，其中每部分包含25%的数据。通常所说的四分位数是指处在25%位置上和75%位置上的两个数值。
计算四分位数时，首先对数据进行排序，然后确定四分位数所在的位置，该位置上的数值就是四分位数。四分位数位置的确定方法有多种，每种方法得到的结果可能会有一定差异，但差异不会很大。

四分位数计算方法：
设25%位置上的四分位数为Q25%，75%位置上的四分位数为Q75%，四分位数位置的计算公式（R对应的为type=6）为：

Q25%位置= (n+1)/4 Q75%位置= 3(n+1)/4

    如果位置是整数，四分位数就是该位置对应的数值；如果是在整数加0.5的位置上，则取该位置两侧数值的平均数；如果是在整数加0.25或0.75的位置上，则四分位数等于该位置前面的数值加上按比例分摊的位置两侧数值的差值。

R软件可以很简单地得到这些结果,求均值、中位数、众数、α 分位数的函数分别是mean ( ) 、median()、mode()、quantile()。

例题1：
15名员工的月工资数据见下表，计算员工的月工资均值、中位数等

首先录入数据：

salary=c(2000,2100,2200,2350,2500,2900,3500,3800,2600,3300,3200,4000,4100,3100,4200)

求各个集中趋势统计量：

mean(salary) #求均值

[1] 3056.667

median(salary) #求中位数 

[1] 3100

mode(salary) #求众数

[1] “numeric”

quantile(salary, probs=c(0,25,50,75,100)/100,type=6)  #求分位数数,probs为分位数向量

0% 25% 50% 75% 100%
2000 2350 3100 3800 4200

在Q25%和Q75%之间大约包含了50%的数据。因此就上面15个员工的薪水而言，可以说大约有一半的薪资在2350~3800分之间。

在R里还提供了fivenum()对数值数据五等分法和 summary ( ) 求出分位数。

summary(salary)

Min. 1st Qu. Median Mean 3rd Qu. Max.
2000 2425 3100 3057 3650 4200

通过上述分析，可以知道公司员工的平均工资为3056.667元，中位数为3100元，75%分位数为3650等信息，从而了解这些员工的工资集中状况。

值得注意的是，均值描述集中趋势往往基于正态分布。如果数据是长尾或有异常值时，这时用均值就不合适。
例如，求平均工资时如果包括了一个经理的月工 资20000元，远远大于普通员工的工资，这时用工 资均值反映员工的平均工资水平，显然是偏大。

salarym=c(salary,20000)
mean(salarym)  

[1] 4115.625

加上经理的工资后，该部门的平均工资从原来的3056.667元变成了4115.625元。这样得到的部门的平均工资显然是不合理的。

median(salarym) 

[1]3150
而此时的中位数为3150元，没有太大变化。因此用中位数来描述集中趋势则是稳健的，不易受异常值影响。

还可以利用截尾均值(trimmed mean) ，比如对该部门的工资截去两头的20%数据后计算均值。用R软件计算截尾均值很简单，只要在mean()中对 trim参数进行设置就可以了

mean(salarym,trim=0.2)

[1] 3125
注意trim可以省略，可以直接写上要截尾的比例。对工资截去两头50%后的均值，实际上就是中位数

mean(salarym,trim=0.5)  

[1] 3150

离散程度

数据沿着中心位置的变化信息可以帮助我们形象化数据集的形状。
用来度量数据离散程度的度量方法称为尺度统计量(scale statistics)，也称为散度统计量
主要有极差、四分位数间距、方差、标准差和变异系数。

离散程度–极差

极差(range)是一组数据的最大值和最小值的差，也称为全距。
一组数据的差异越大,其极差也越大。
类似于极差， 四分位数间距或四分位数极差 (interquantile range)定义为上下四分位数之差， 也就是箱线图盒子的长度。它描述了中间半数观测值的散布情况。

离散程度–四分位数极差

四分位数极差它是上四分位数（QU，即位于75%）与下四分位数（QL，即位于25%）的差。计算公式为：IQR =QU-QL
四分位差反映了中间50%数据的离散程度，其数值越小，说明中间的数据越集中；其数值越大，说明中间的数据越分散。四分位差不受极值的影响。此外，四分位差主要用于测度顺序数据的离散程度。对于数值型数据也可以计算四分位差，但不适合分类数据。
极差和四分位数极差实际上各自只依赖于两个值,信息量太少。

离散程度–方差

另一种利用偏差构建的统计量：方差(variance)是更为受欢迎的一种变异性的度量指标。 如果观测样本为 x1,…,xn,那么样本方差定义为:

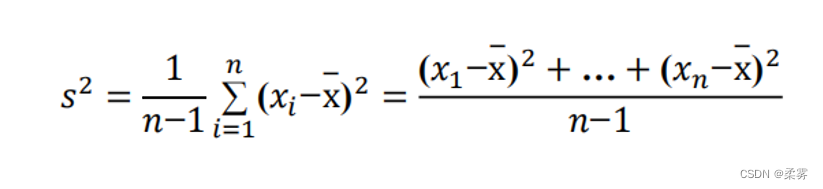
离散程度–加权方差

设数据x1,x2,…,xn相应的频数分别为w1,w2,…,wn, 则它们的加权方差(weighted variance)的计算公式

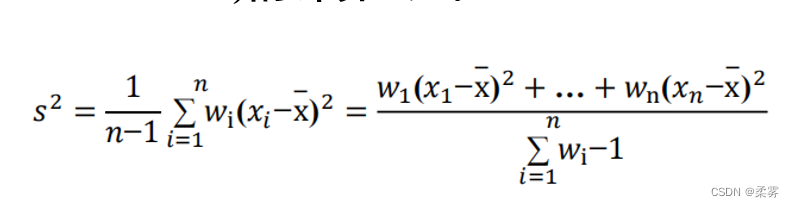
显然,方差越大,则数据的分散程度就越大。

离散程度–标准差

由于方差的量纲是原始数据量纲的平方，为了保持量纲不变,人们常用方差的算术平方根作为基本等价的尺度统计量
样本方差的平方根称为样本标准差(sample standard deviation),记为

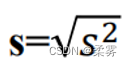
标准差可以度量一个数据集的变异性：
1.标准差越大,数据的变异性越大。
2.标准差越小,数据的变异性越小。

离散程度–变异系数

能直接比较两个或多个离散性的度量结果吗?
比如能否比较员工月收入分布的标准差与同一组员工每月旷工天数分布的标准差的大小?
为了对收入和旷工天数这两个或多个数据的离散性进行比较, 可以使用变异系数(coefficient of variation,CV)
变异系数是标准差与均值的比值，公式为：

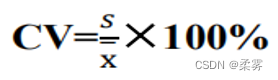
变异系数可以对比分析不同水平的变量数据之间标志值的变异程度。
变异系数可以对比分析不同类型（收入和旷工天数）的数据的离散性。对相同类型的数据，当均值相去甚远（如大象的体重和老鼠的体重）时，也可以使用变异系数。但是使用变异系数的前提条件是只适用于仅含正数的连续型变量。

方差、标准差的函数分别是var()和sd()。
变异系数是标准差与均值的比值，可以使用 sd()/mean()得到。
极差使用diff(range())，因为range()得到的是数据的极大值和极小值。

方差、标准差对异常值也很敏感，这时可以用 稳健的四分位间距(IQR)来描述离散程度

IQR(salarym,type=6) 

[1] 1450

数据的形状

数据的形状–偏度

偏度Sk (skewness)描述观测数据分布形态的偏斜方向和程度

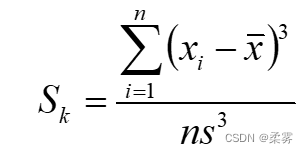
当Sk=0时，呈对称分布；当Sk >0时，呈正偏态分布或右偏态分布(在分布的右侧有长尾);当Sk <0时，呈负偏态分布或左偏态分布(在分布的左侧有长尾)。
偏度系数越接近0，偏斜程度就越低也就越接近对称分布。若偏度系数大于1或小于-1，视为严重偏斜分布；若偏度系数在0.5-1或-1- -0.5之间，视为中等偏斜分布；若偏度系数小于0.5或大于-0.5，视为轻微偏斜。

数据的形状–峰度

峰度 (kurtosis)描述观测数据分布形态的陡缓程度

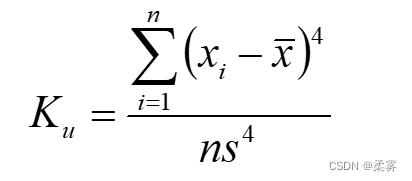
当 等式为0时，数据的分布形态与标准正态分布的陡缓程度相同；当 等式 >0时，数据的分布形态比标准正态分布的高峰陡峭；当 等式 <0时，数据的分布形态比标准正态分布的高峰平缓，数据相对分散。

例2.9继续。计算工资数据的偏度和峰度

salary=c(2000,2100,2200,2350,2500,2900,3500,3800,2600,3300,3200,4000,4100,3100,4200)
install.packages("moments")
library(moments) 

skewness(salary) [1] 0.117456
kurtosis(salary) [1] 1.683055
该工资数据呈右偏态分布，轻微偏斜；并且数据的分布形态比正态分布的高峰陡峭。

练习

1、为了解消费者对不同行业的满意度，随机调查了120个消费者，得到一些有关数据（提供数据，不用自己录入exercise2_1.RData）
（1）生成简单频数分布表

load("C:ch2/exercise/exercise2_1.RData")
summary(exercise2_1)
d1<-table(exercise2_1$行业)
d1
d2<-table(exercise2_1$性别)
d2
d3<-table(exercise2_1$满意度)
d3

（2）绘制简单条形图、复式条形图对各类别的频数进行分析

barplot(d1,xlab="行业",ylab="频数",main="(a)垂直条形图")
barplot(d2,xlab="性别",ylab="频数",main="(a)垂直条形图")
barplot(d3,xlab="满意度",ylab="频数",main="(a)垂直条形图")
d4<-table(exercise2_1$满意度,exercise2_1$行业)
d4
bar1<-barplot(d4,xlab="行业",ylab="频数",ylim=c(0,30),col=c("red","green"),legend=rownames(d4),args.legend=list(x=12),beside=TRUE,main="(a)行业并列条形图")

（3）绘制饼图和扇形图（查阅资料后作答）对各类别的百分比进行分析

count1<-table(exercise2_1$行业)
name<-names(count1)
name
percent<-prop.table(count1)*100
label1<-paste(name," ",percent,"%",sep=" ")
pie(count1,labels=label1)

count2<-table(exercise2_1$行业)
count2

电信业 航空业 金融业 旅游业
38 19 26 37

library(plotrix)
name<-names(count2)
percent<-count2/sum(count2)*100
labs<-paste(name," ",percent,"%",sep="")
fan.plot(count2,labels=labs)

2、随机抽取50个网络购物的消费者，调查他们某月的网购金额，结果如下（提供数据exercise3_1，不用自己录入）：
（1）计算平均数、标准差、极差和四分位差

load("C:/example/ch2/exercise/exercise3_1.RData")
mean(exercise3_1$网购金额)

[1] 1032.64

sd(exercise3_1$网购金额)

[1] 385.3728

R<-diff(range(exercise3_1$网购金额));R

[1] 1981

quantile(exercise3_1$网购金额,probs=c(0.25,0.5,0.75),type=6)

25%     50%     75% 

825.75 985.50 1248.50

（2）计算10%，25%，50%，75%，90%的分位数

quantile(exercise3_1$网购金额,probs=c(0.1,0.25,0.5,0.75,0.9),type=6)

10%     25%     50%     75%     90% 

532.20 825.75 985.50 1248.50 1490.90

（3）计算偏度系数和峰度系数，分析网购金额的分布特点

install.packages("agricolae")
library(agricolae)
skewness(exercise3_1$网购金额)#偏度系数

[1] 0.6633022 #中等偏度分布并呈正偏态分布(在分布的右侧有长尾)

kurtosis(exercise3_1$网购金额)#峰度系数，尖峰分布

[1] 1.220335

代码007普通

打赏 收藏 海报 链接