统计学-R语言-4.5

前言

本篇文章将继续对数据的类型做介绍，本片也是最后一个介绍数据的。

多变量数据

掌握描述多变量数据的分析方法：多维列联表、复式条形图、并列箱线图、点带图、多变量散点图（重叠散点图和矩阵式散点图）。

多维列联表

除了一维表、二维表，在实际中更多的是多维表，也就是多个变量交叉生成的表格。
R中的table()函数也可以生成多维表。
假设存在x、y、z三个变量，table(x,y)则生成x、 y二维表，table(x,y,z)生成每个z值关于x、y的二维表（由于计算机作三维及三维以上的表格不方便，所以就用这种方式显示）。

例题1：
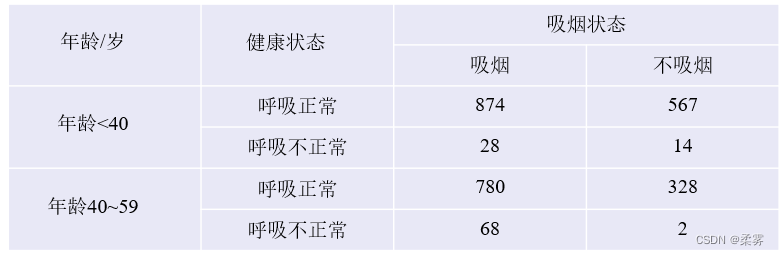
为了了解不同年龄的男性，吸烟与呼吸系统疾病之间的关系，青原博士获得如下的调查数据。

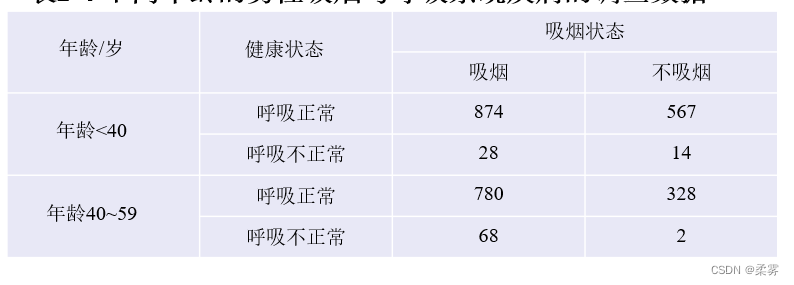
这是一个2×2×2的三维列联表，因为每个变量的水平数均为2。

age=c(rep("40岁",4),rep("40~59",4))
smoke=rep(c("吸烟","不吸烟"),4)
breath=rep(c("呼吸正常","呼吸正常","呼吸不正常","呼吸不正常"),2)
freq=c(874,567,28,14,780,328,68,2)

接下来分析breath变量的频数分布，分析后再作breath与smoke的二维表，最后作breath、smoke与age的三维表

xtabs (freq~breath)

breath
呼吸不正常 呼吸正常
112 2549

xtabs(freq~breath+smoke)        

smoke
breath 不吸烟 吸烟
呼吸不正常 16 96
呼吸正常 895 1654

xtabs(freq~breath+smoke+age)

, , age = <40岁
smoke
breath 不吸烟 吸烟
呼吸不正常 14 28
呼吸正常 567 874
, , age = 40~59
smoke
breath 不吸烟 吸烟
呼吸不正常 2 68
呼吸正常 328 780

复式条形图

对breath按不同的smoke作复式条形图。
从下图可以看出，首先按smoke分成”吸烟”，“不吸烟” 2组，每组里又按breath分成”呼吸正常”，”呼吸不正常”2类

par(mfrow=c(1,2))
barplot(xtabs(freq~breath+smoke))
barplot(xtabs(freq~breath+smoke),beside=T)

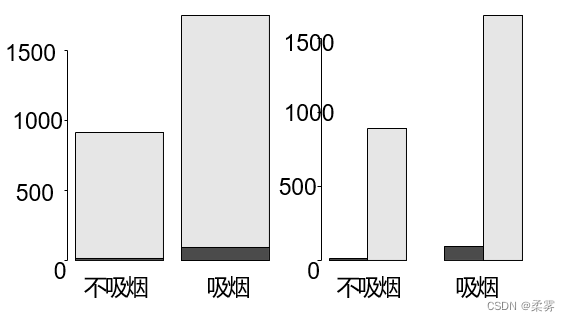
breath按照smoke作的复式条形图，黑色的方块代表不健康。

对smoke按照不同的breath做复式条形图，首先按breath分 成“呼吸正常”，“呼吸不正常”2组；然后，每组里又分成“吸烟”，“不吸烟”等2类。结果如下图所示

par(mfrow=c(1,2))
barplot(xtabs(freq~smoke+breath))
barplot(xtabs(freq~smoke+breath),beside=T)

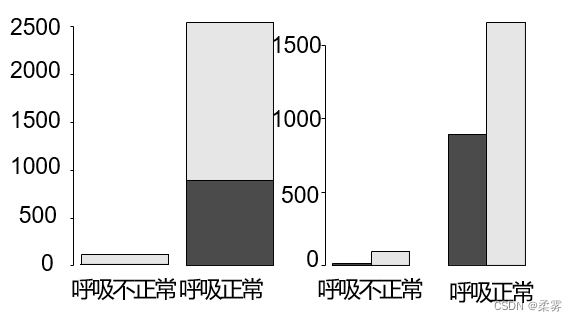
黑色的方块代表不吸烟。

并列箱线图

用并列箱线图考察年龄与吸烟、年龄与呼吸的关系
为了画出并列箱线图，此处需要没有分组的年龄变量。 不失一般性，假设两个年龄段”<40岁”,”40~59″的男性的年龄均值分别为20岁和49.5岁
按照下面的程序产生年龄的连续观测值

set.seed(500)
age.value=round(c(rnorm(1483,mean=20,sd=6.5),rnorm(1178,mean=49.5,sd=3)))

set.seed()函数是为了保证随机生成的随机数前后一致
首先，不设置该种子函数

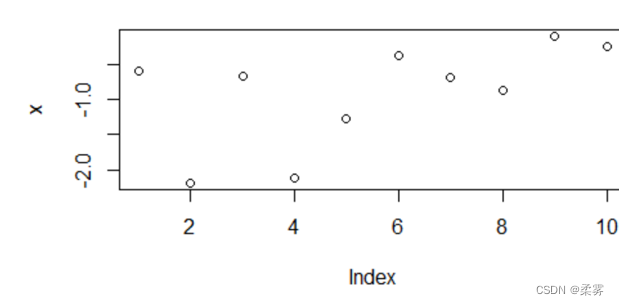
x=rnorm(10)
plot(x)

绘出的图如下：

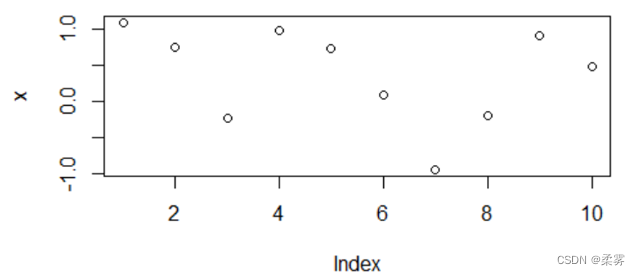
重新运行一遍这两行，就是另外的图

x=rnorm(10)
plot(x)

为了在下次运行时，产生一样的随机数，就得使用set.seed()函数了，如下

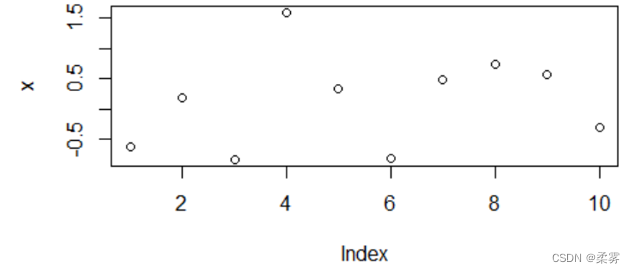
set.seed(1)
x=rnorm(10)
plot(x)

画图如下：

那么此时，我们重复运行上面的代码

set.seed(1)
x=rnorm(10)
plot(x)

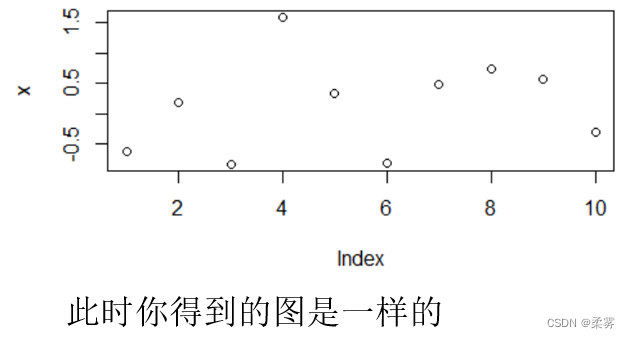
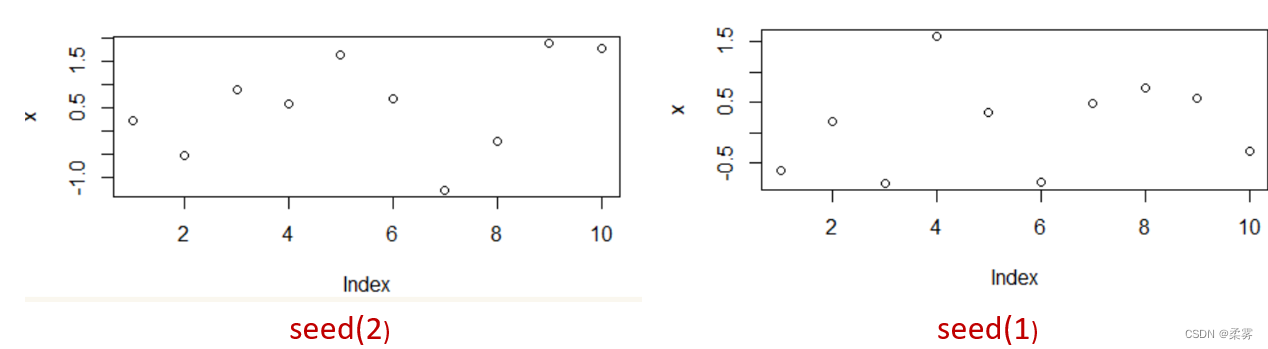
那么set.seed(1)换为set.seed(2)时还一样吗？我们运行下面程序

set.seed(2)
x=rnorm(10)
plot(x)

显然是不一样的，因此，set.seed()括号里面的参数可以是任意数字，是代表你设置的第几号种子而已，不会参与运算，是个标记而已。

rnorm(n, mean = 0, sd = 1)
n 为产生随机值个数（长度），mean 是平均数， sd 是标准差 。
使用该函数的时候后，一般要赋予它 3个值.
rnorm（） 函数会随机正态分布，然后随机抽样或者取值 n 次，
rnorm（5,0,1） 以N（0,1）的正态分布，分别列出5个值。

函数形式：rep(x, time = , length = , each = ,)
参数说明：
x：代表的是你要进行复制的对象，可以是一个向量或者是一个因子。
times：代表的是复制的次数，只能为正数。负数以及空值都会为错误值。复制是指的是对整个向量进行复制。
each：代表的是对向量中的每个元素进行复制的次数。
length.out：代表的是最终输出向量的长度。

例题1：
用并列箱线图考察年龄与吸烟、年龄与呼吸的关系
为了画出并列箱线图，此处需要没有分组的年龄变量。 不失一般性，假设两个年龄段”<40岁”,”40~59″的男性的年龄均值分别为20岁和49.5岁
按照下面的程序产生年龄的连续观测值

set.seed(500)
age.value=round(c(rnorm(1483,mean=20,sd=6.5),rnorm(1178,mean=49.5,sd=3)))

还需要给出每一个男性的吸烟状态、呼吸状态,这由下面的程序来实现：

age1=c(rep("<40岁",1483),rep("40~59",1178))
breath1=c(rep(" 呼吸正常",1441),rep("呼吸不正常",42),rep(" 呼吸正常",1108),rep("呼吸不正常",70))
smoke1=c(rep("吸烟",874),rep("不吸烟",567),rep("吸烟",28),rep("不吸烟",14),rep("吸烟",780),rep("不吸烟",328),rep("吸烟",68),rep("不吸烟",2))
基于age.value，分别做出age.value按smoke1和breath1分类的箱线图
par(mfrow=c(1,2))
boxplot(age.value ~smoke1)
boxplot(age.value ~breath1)

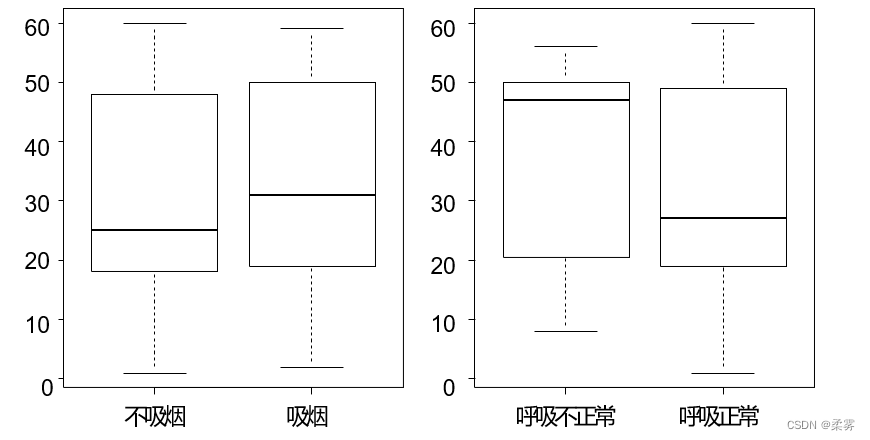
从箱线图可以发现，吸烟的男性平均年龄高于不吸烟的男性，呼吸不正常的男性平均年龄高于呼吸正常的男性。

例题2：
为了比较乘坐公交车上班快还是自己开车快，青原博士对两种方式所用时间各进行了10次记录，具体数据见下表。

目的是比较两种交通方式所需时间是否有差异，从并列箱线图可以看出两个交通方式所需时间存在较大差异

x1=c(48,47,44,45,46,47,43,47,42,48)
x2=c(36,45,47,38,39,42,36,42,46,35)
time=c(x1,x2)
transportation=c(rep(1,10),rep(2,10))
traffic.time=cbind(time,transportation)
boxplot(time ~transportation

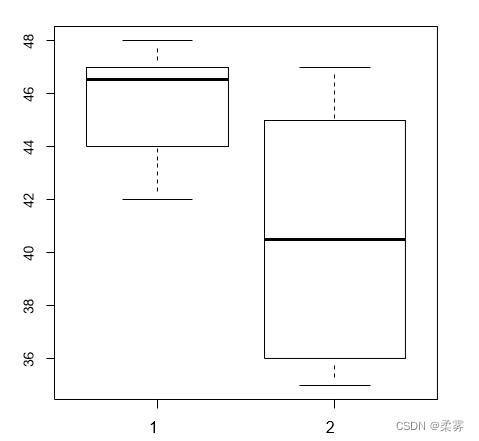
cbind： 根据列进行合并，即叠加所有列，m列的矩阵与n列的矩阵cbind()最后变成m+n列，合并前提：cbind(a, c)中矩阵a、c的行数必需相符。
rbind： 根据行进行合并，就是行的叠加，m行的矩阵与n行的矩阵rbind()最后变成m+n行，合并前提：rbind(a, c)中矩阵a、c的列数必需相符。


例题三：
模拟1000个标准正态分布随机数，分成10组，作10个并列箱线图这里利用rep()函数重复100次生成1:10的1000个数，再利 用factor()函数生成10个因子。

r1= rnorm(1000)
f1=factor(rep(1:10,100))
boxplot(r1~f1)

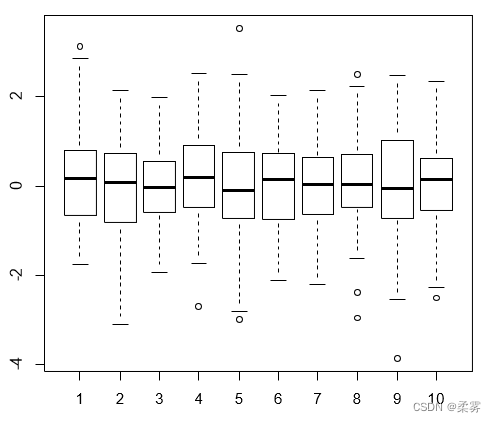
R语言中取整运算主要包括以下五种：

floor()：向下取整；ceiling(): 向上取整；round(): 四舍五入取整；turnc(): 向0取整；signif(): 保留给定位数的精度。
floor返回对应数字的’地板’值，即不大于该数字的最大值；
ceiling返回对应数字的’天花板’值，就是不小于该数字的最小整数；
round是R里的’四舍五入’函数，round的原型是round(x, digits = 0), digits设定小数点位置，默认为零即小数点后零位(取整)。
trun的特性是’向零截取’， 也就是说对于一个数字a，它将数轴分成两侧，trunc(a)将返回数轴上包含数字0的那一侧离a最近的那个整数。
signif是保留有效数字的函数。常用于科学计数。

点带图

点带图（StripChart）经常用来比较各变量的分布情况，点带图主要用在当样本观测值较少时。
R作点带图的函数是stripchart()，对于双变量数据其用法是stripchart(z~t)，z变量在t变量上的分布情况，不同的是这里z变量刻度在x轴上，而t 变量在y轴上。

例题1：
对呼吸正常与否按吸烟与否分类作点带图。
结果如下图所示，呼吸的各个类型都描在了图上。

smoke1[ smokel1=="吸烟"]=1
smoke1[ smokel1=="不吸烟"]=0
par(mfrow =c(1,1))
stripchart（as. numeric（ smoke1）~ breath1，xlab="吸烟"）

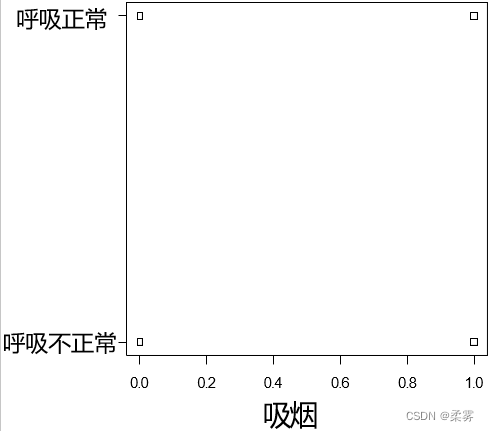
x轴用1 ， 0 代表” 吸烟” 和”不吸烟”等2组
该例中的两个变量都是二分类，关系比较简单。下面再看一个复杂一点儿的点带图例子。

一般只要是数字，不管是什么类型的，都可以通过as.numeric()函数转换为对应的numeric类型的数字，例如
x<-“123”，x为character类型，而as.numeric(x)则为numeric类型的123。
但是因子(factor)类型却不一样。
a<-factor(c(100,200,300,301,302,400,10))，
它们的值分别为100 200 300 301 302 400 10，然而as.numeric(a)对应的值并非100 200 300 301 302 400 10，而是2 3 4 5 6 7 1。
因子(factor)转换成数值型(numeric)的规则是这样的：
一共有n个数，那么转换后的数字就会在1—n中取值，数字最小的取一，次小的取二，以此类推。那么如何让因子(factor)类型里的数值转换对应的数值型呢？

mean(as.numeric(as.character(factorname)))
mean(as.numeric(levels(factorname)[factorname]))

以上代码就可以实现将因子(factor)类型里的数值转换对应的数值型，思路都是先转换成字符型然后再转换成数值型。

例题2：
模拟100个标准正态分布的随机数，分成5组，作点带图

r2= rnorm(100)
f2=factor(rep(1:5,20))
stripchart(r2~f2)

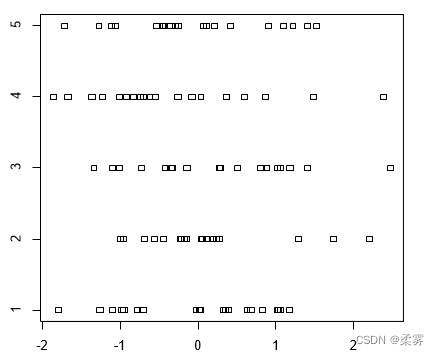
反映了各随机数在各组上的分布情况，而且绝大 部分集中在[-1,1]上，当样本观察值较多时，点带图就显得有点凌乱，没有箱线图清晰直观。这是点带图的局限性，当样本观察值较多时，建议使用箱线图。

多变量散点图

多变量散点包括重叠散点图和矩阵式散点图。我们使用R自带的著名的鸢尾花（iris）数据集来介绍如何绘制多变量散点图。

例题1：
R内置的鸢尾花(iris）数据集是Fisher关于 150个植物分类的数据，是判别分析的经典案例。
该数据集内有五个变量：Sepal.Length（花萼长度）、 Sepal.Width（花萼宽度）、Petal.Length（花瓣长度） Petal.Width（花瓣宽度）、Species（品种）。
品种有三个：setosa，versicolor和virginica。每种品种有50 个样本。

iris
levels(iris $ Species)#种类的水平

[1] “setosa” “versicolor” “virginica”

共有三种植物，
分别是setosa，versicolor和virginica
为了在图中方便显示，
重新标示它们为1、2和3

iris.lab=rep(c("1","2","3"),rep(50,3))

重叠散点图

有时出于研究的需要，将两个或多组两个变量的散点图绘制在同一个图中， 可以更好的比较它们之间的相关关系,这时就可以绘制重叠散点图

par(mfrow=c(1,2))
plot(iris[,1],iris[,3],type="n")	#绘制iris第1列和第3列的散点图，type="n"不显示点
text(iris[,1],iris[,3],cex=0.6) #显示样本序号，缩小字体cex=0.6
plot(iris[,1],iris[,3],type="n")
text(iris[,1],iris[,3],iris.lab,cex=0.6)

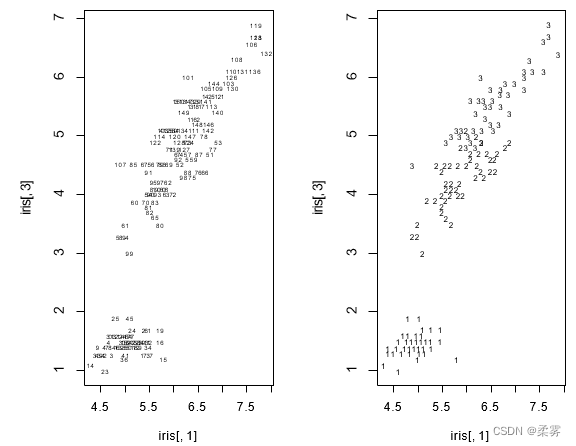
矩阵式散点图

同时考察三个或三个以上的数值变量间的相关关系时， 一一绘制它们之间的简单散点图就十分麻烦
利用矩阵式散点图则比较合适，这样可以快速发现多个 变量间的主要相关性，这一点在多元线性回归中显得尤为重要
R作矩阵式散点图的函数是pairs()。

pairs(iris)
pairs(iris [1:4],pch=21,bg=iris.lab)	#按iris.lab分类

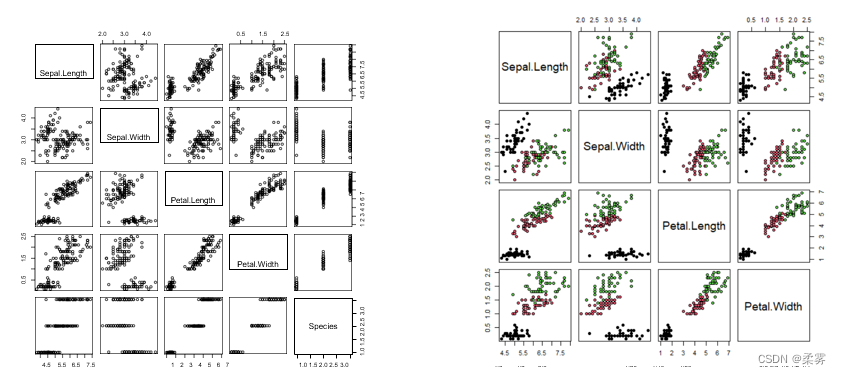
练习

1、（数据： example2_4. RData）下表是随机抽取的20家医药企业销售收入、销售网点数、销售人员数以及广告费用的数据。

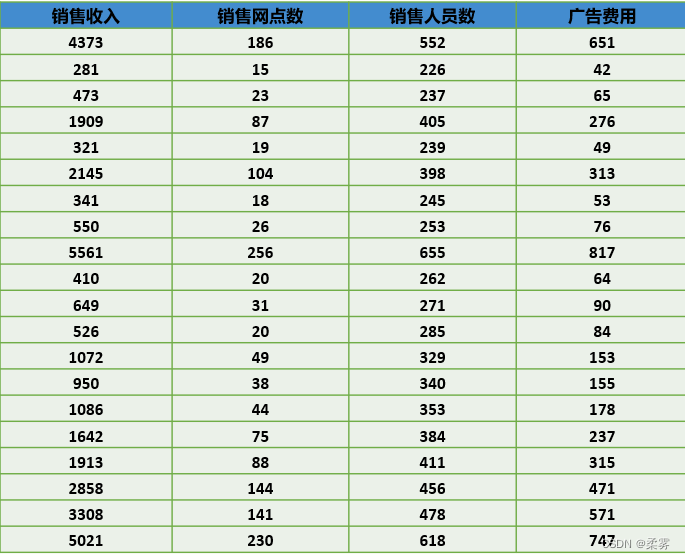
1 . 绘制带有箱线图的散点图观察这些变量间的关系，并描述每个变量的分布状况

par(fig=c(0,0.8,0,0.8),mai=c(0.9,0.9,0.1,0.1)) 
plot(广告费用,销售收入,xlab="广告费用",ylab="销售收入",cex.lab=0.7,cex.axis=0.7)
abline(lm(销售收入~广告费用,data=example2_4),col="red")
par(fig=c(0,0.8,0.5,1),new=TRUE)
boxplot(广告费用,horizontal=TRUE,axes=FALSE)
par(fig=c(0.52,1,0,0.9),new=TRUE)
boxplot(销售收入,axes=FALSE)

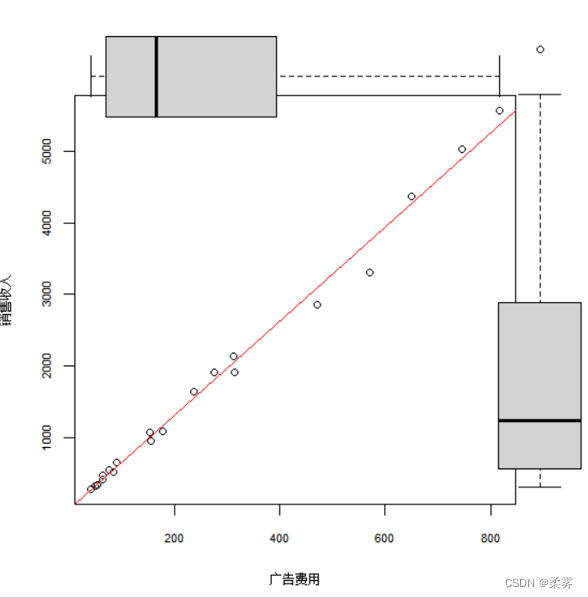
从图中的两个箱线图可以看出，销售收入和广告费用均为右偏分布。

2 . 绘制关于销售收入与销售网点数、销售人员数及广告费用的重叠散点图

par(mai=c(0.5,0.85,0.1,0.1))
plot(广告费用,销售收入,xlab="",ylab="销售收入")
abline(lm(销售收入~广告费用,data=example2_4))
points(销售网点数,销售收入,pch=2,col="blue")
abline(lm(销售收入~销售网点数,data=example2_4),col="blue")
points(销售人员数,销售收入,pch=3,col="red")
abline(lm(销售收入~销售人员数,data=example2_4),col="red")
legend("bottomright",legend=c("广告费用","销售网点数","销售人员数"),pch=1:3,col=c("black","blue","red"))

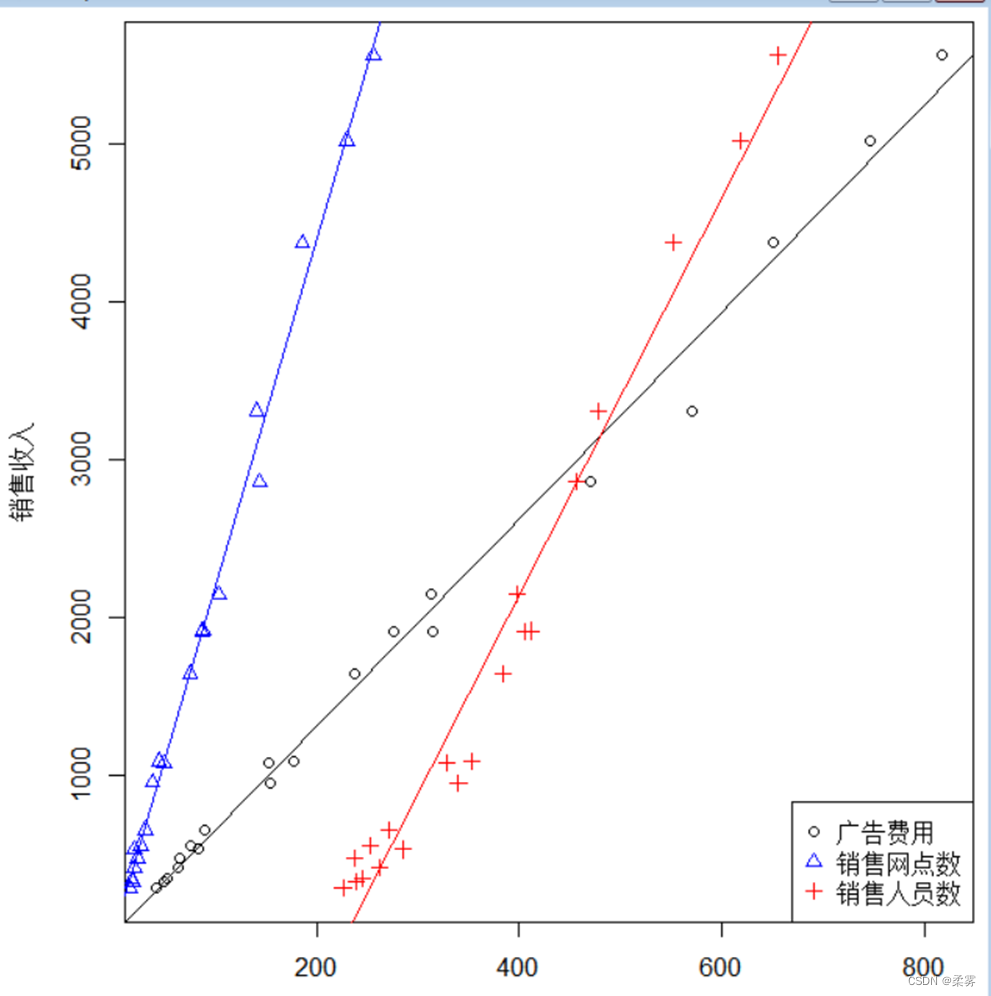
3 . 绘制矩阵散点图

load("C:/example/ch2/example2_4.RData")
plot(example2_4,cex=0.8,gap=0.5) 
pairs(example2_4)

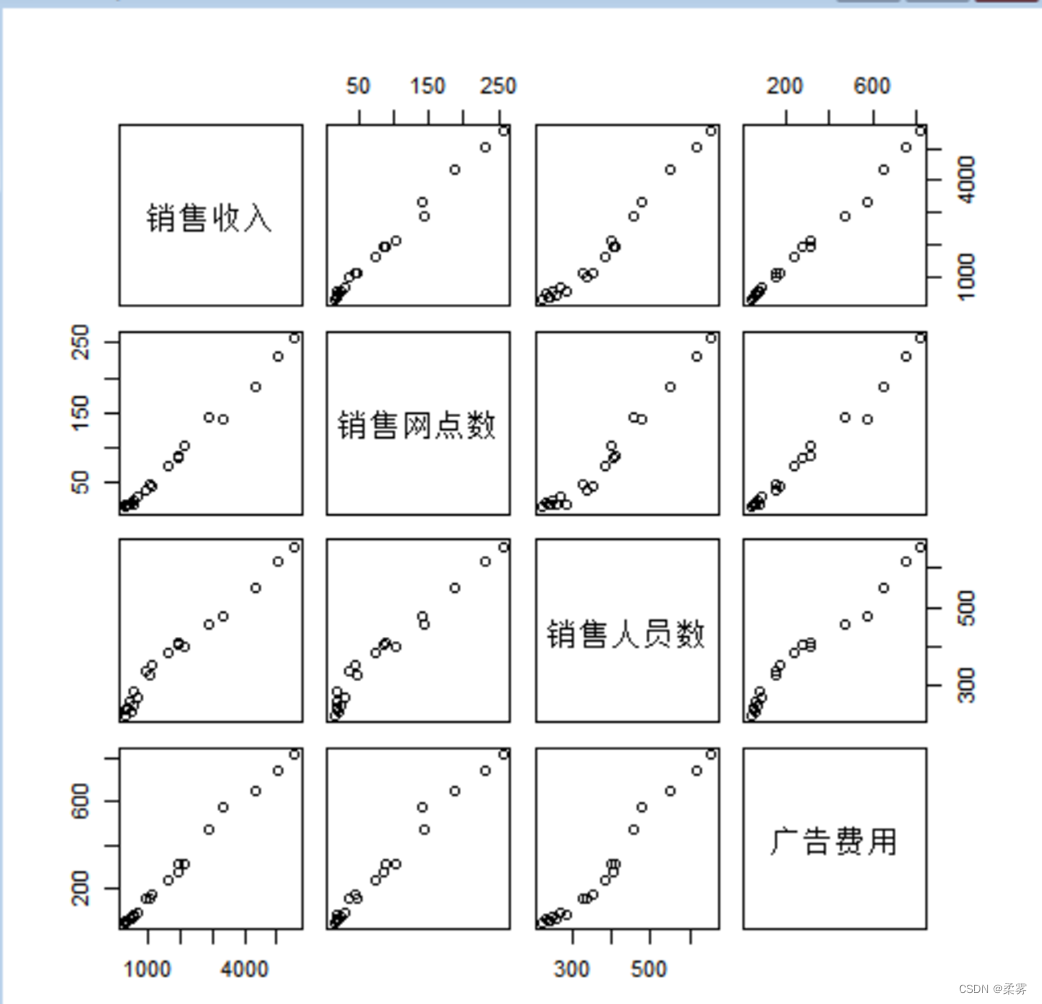
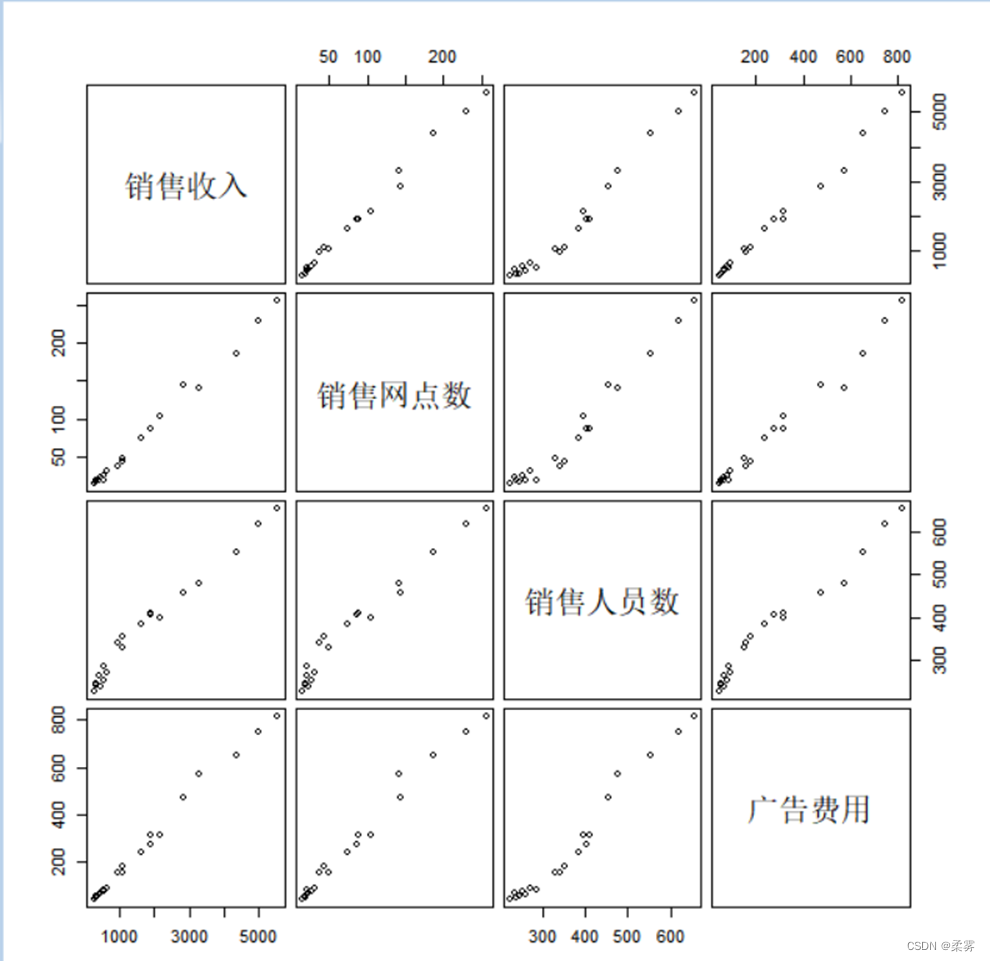
图显示，销售收入、销售网点数、销售人员数、广告费用两两之间都有较强的线性关系。

代码007普通

打赏 收藏 海报 链接