引言
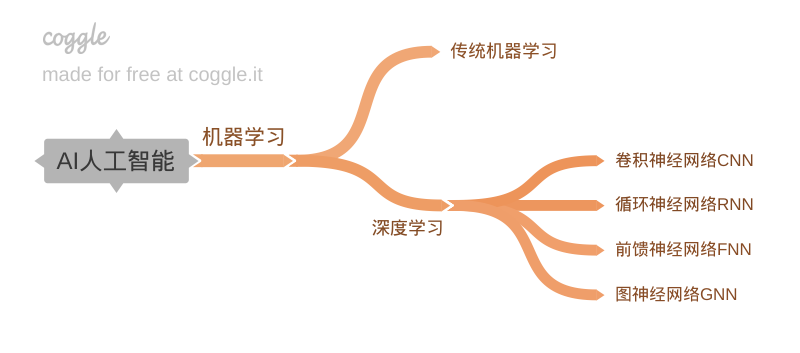
深度学习的四个分支对应了四种常见的数据格式,前馈神经网络FNN处理表格数据,表格数据可以是特征向量,卷积神经网络CNN处理图像数据,循环神经网络RNN处理时序数据,图神经网络GNN处理图数据。
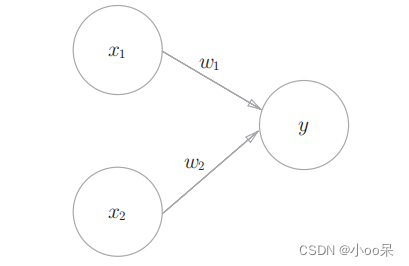
这里的FNN指的是如下图所示的带有输入层,隐藏层,输出层的网络。
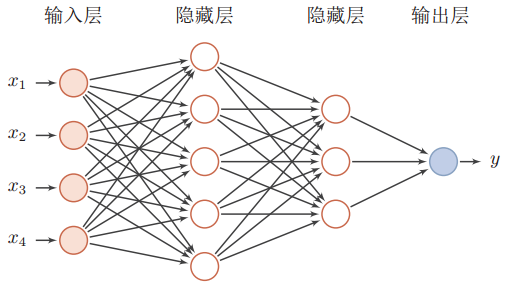
但这四种对应关系并不是一成不变。
声音文本这类时序数据,用RNN类型的网络最适合,但如果你把一个句子当作一个1*N的矩阵,那就可以用CNN处理了,只不过,CNN需要堆叠多个层来抓取时序数据中的上下文信息,这在图像领域被称为感受野。
注意:虽然可以通过一定的技巧把句子表示成矩阵然后用CNN处理,但从本质上来说,CNN还是不如RNN更适合处理时序数据。
如果将图像划分成patch,这些pathces组成序列,同样也可以用Transformer处理,这就是Vision Transformer:ViT。
更准确地说,只要能表示成GNN兼容的图数据结构就能用GNN处理。
今天的文章来自distill发布的一篇博文:A Gentle Introduction to Graph Neural Networks。
网址:https://distill.pub/2021/gnn-intro/B站沐神视频讲解:https://www.bilibili.com/video/BV1iT4y1d7zP/?spm_id_from=333.999.0.0
这篇文章写的非常好,亮点是不光有交互式图表,还有PlayGround,可见作者是下了一番功夫的。
先科普一下什么是Playground?
Playground通常指在机器学习和人工智能领域用来交互式体验和可视化AI模型的一种系统或平台。
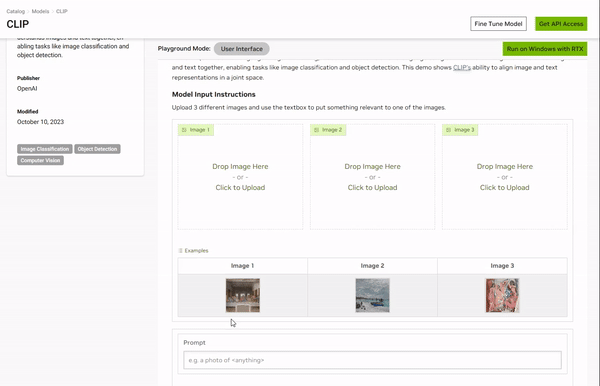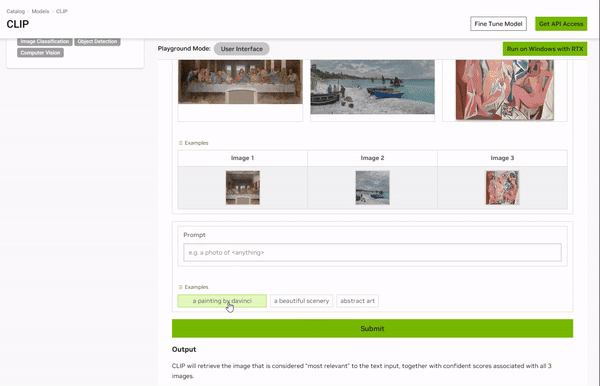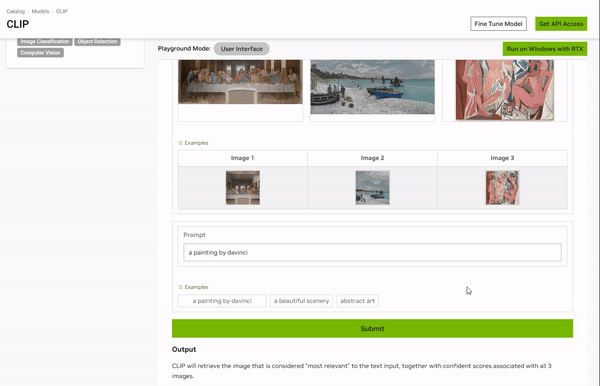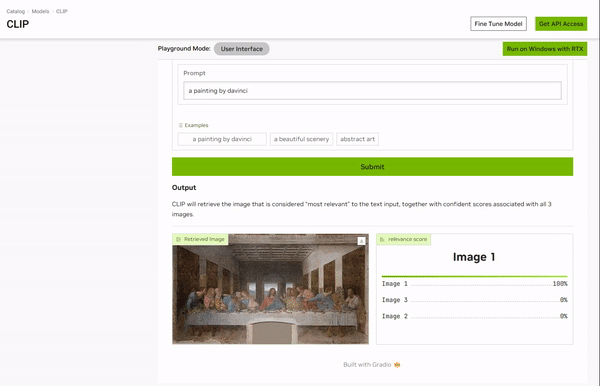
https://catalog.ngc.nvidia.com/orgs/nvidia/teams/playground/models/clip
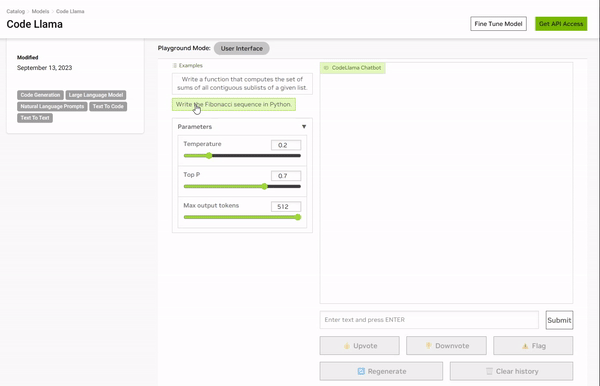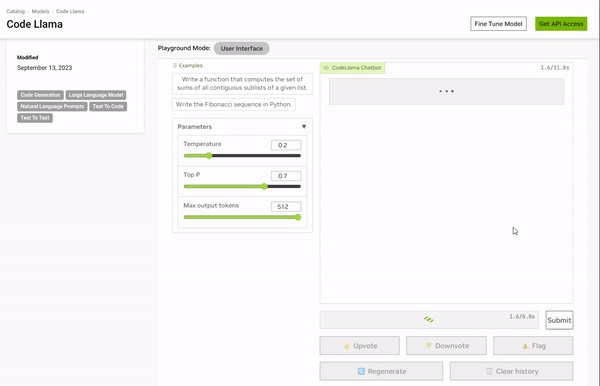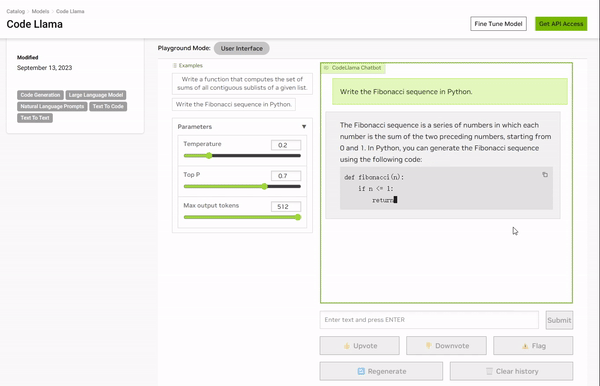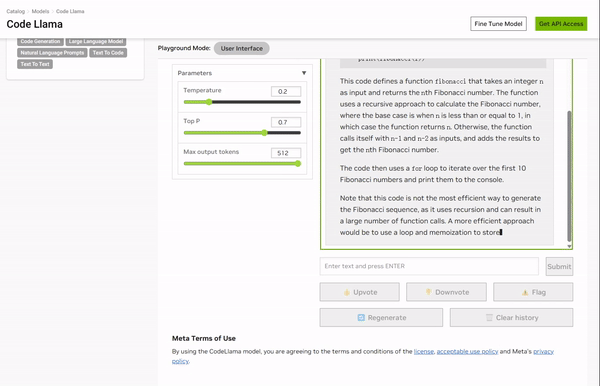
https://catalog.ngc.nvidia.com/orgs/nvidia/teams/playground/models/codellama
NVIDIA NGC或者Hugging face上有更多好玩的AI Playground,大家可以亲自去体验一下。https://huggingface.co/
但我不会将上面的文章原样照搬过来,而是进行概括性的总结,大家一定一定去阅读原文,因为原文里有大量的交互式图表和Playground,能加速对GNN的理解。
今天的主角是GNN,而GNN处理的对象是图Graph。跟其它神经网络一样,在其出现之前,都有传统的方法来处理对应的数据结构。
但是在数据量和算力的加持下,为了完成更复杂的任务,对应的神经网络应运而生,GNN也是如此。
后续内容主要分为四部分
1.什么样的数据可以很自然的表示成图
2.图与其它类型数据的不同之处以及如何应对这种不同
3.构建一个GNN
什么是图?
图也分为有向图和无向图,例如,社交媒体中,如果互相关注了则是无向图,如果像B站这样,我关注了你,但你并没有关注我,则是有向图。

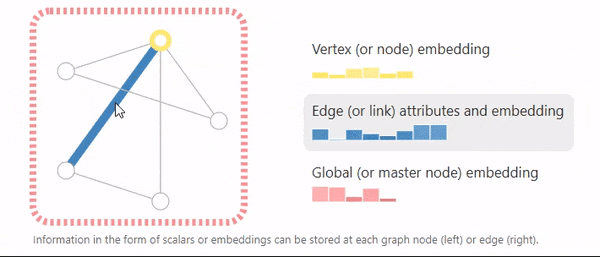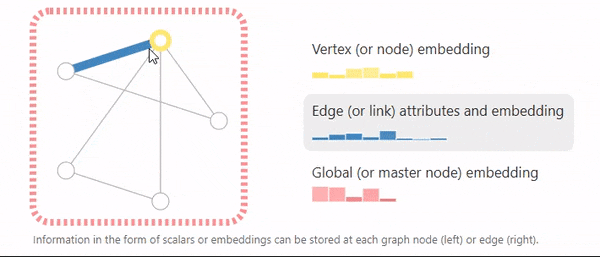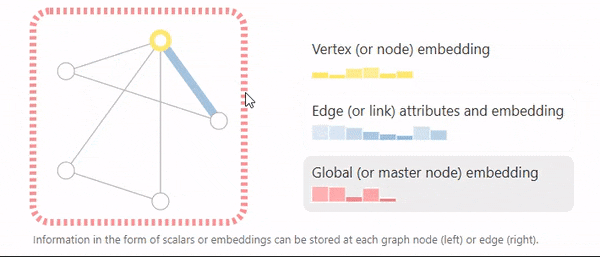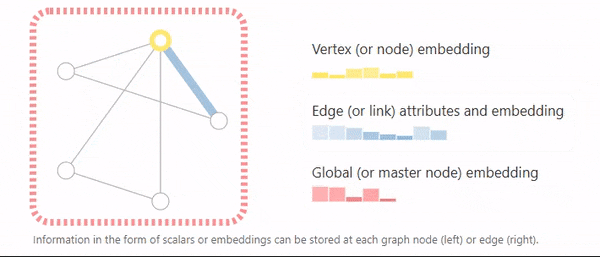
节点有自己的属性,边有自己的属性,整个图也有自己的属性,如上图,属性可以用标量或者向量表示。向量大小可以不一致。
前面已经透漏了GNN可以处理图像和文本,那么图像和文本就可以表示成图。
图像的每个像素即是一个节点,节点的属性自然就是RGB值,相邻像素之间用一条边来表示相邻关系,这里用邻接矩阵来表示连接性。
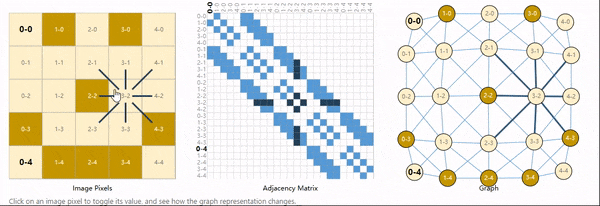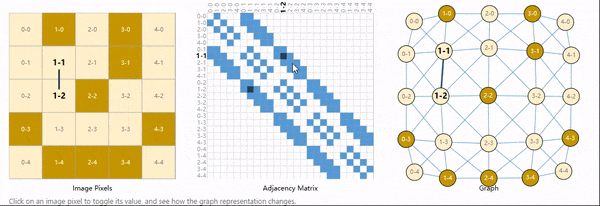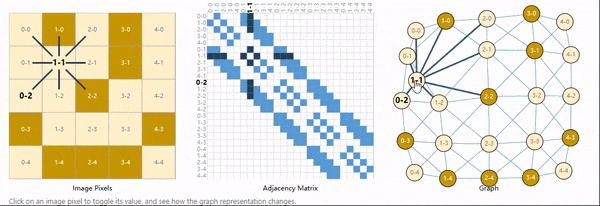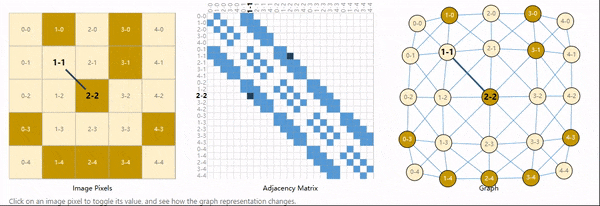
同理,一个句子中每个字符,每个单词,每个Token都可以看作是一个节点,相邻节点之间可以用一条有向边相连,这就构成了一个有向图。
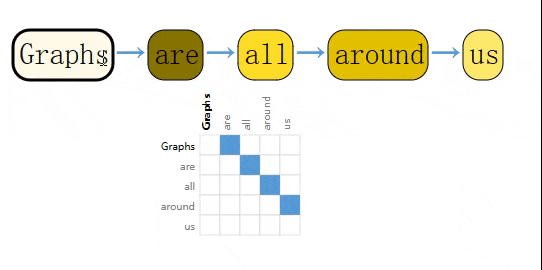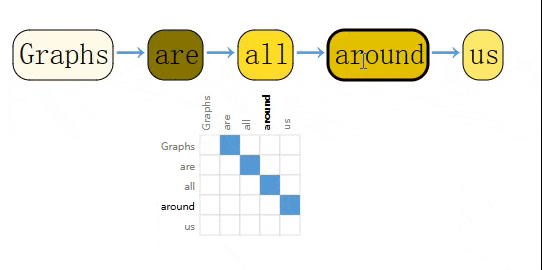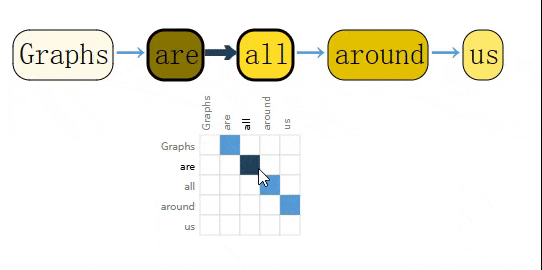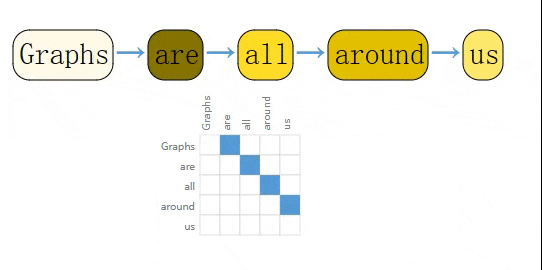
除此之外,还有很多其它数据可以表示成图。
分子由两个或多个原子通过共用电子对构成化学键而连接成一个整体,分子之间不同的连接方式构成了不同的物质。
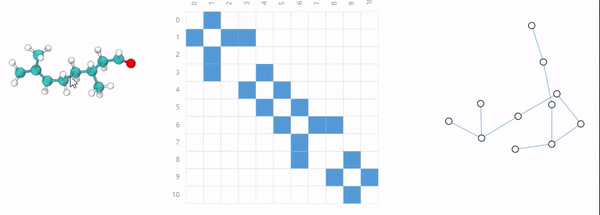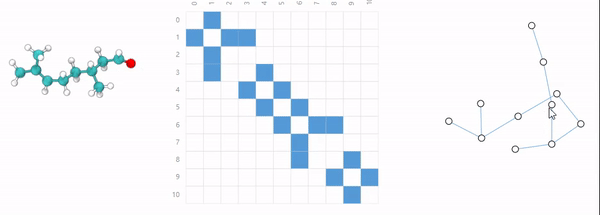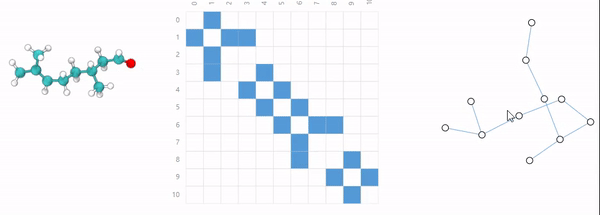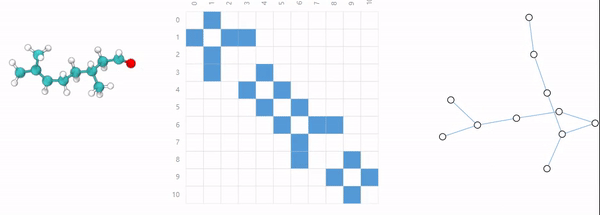
社会是一个大家庭,所有成员和之间的关系构成了一个复杂的社交网络。

如果能够充分利用这个网络,就能发挥巨大价值,例如,知识图谱,推荐系统。
引用关系也可以组织成图,例如,维基百科中每个网页都会列出引用资料。
好了,到此我们已经能够把很多事物表示成图的形式,这样就够用GNN来处理了,那到底能干什么呢?
图层面任务
对图的整体进行预测,GNN输出对整个图的预测属性,例如,下图中分辨出具有两个环的图,这就是一个针对整个图的分类任务。
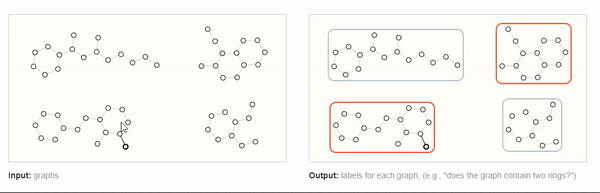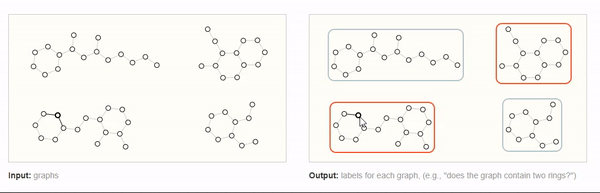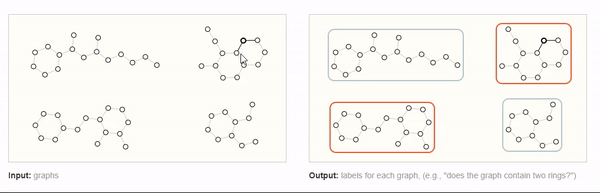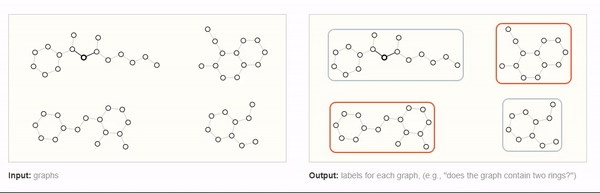
对于图像和文本而言,图层面的任务类似于MINIS数字分类,或者句子情感分析,例如。判断一个句子表达的是正向情绪还是负面情绪。
顶点层面任务
GNN预测图中每一个节点的属性,例如,下图,预测社交网络中的成员是否是诈骗分子。这就是一个节点分类任务。
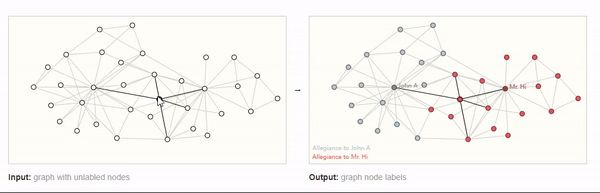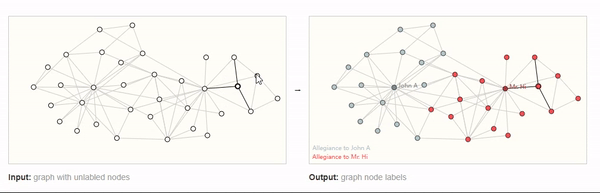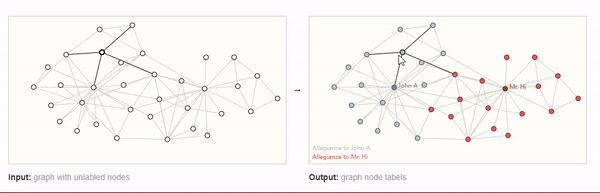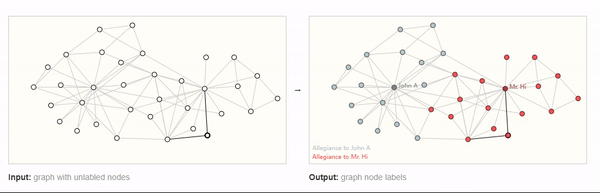
对于图像和文本而言,顶点层面的任务类似于图像分割,图像分割不就是对每个像素分类嘛,对于文本,就是预测句子中每个单词的词性(例如名词、动词、副词等)。
边层面任务
边的存在与否是一种结构属性,也就是连接性,GNN也可以预测图中边的非结构属性,什么是非结构属性?对于一个社交网络而言,边代表节点之间有关系,但如何度量亲疏程度呢?这就涉及边的非结构属性了。
预测亲疏程度是一个回归任务,下图则是一个分类任务,每一条边只能是watching,fighting,standing on中的一种。
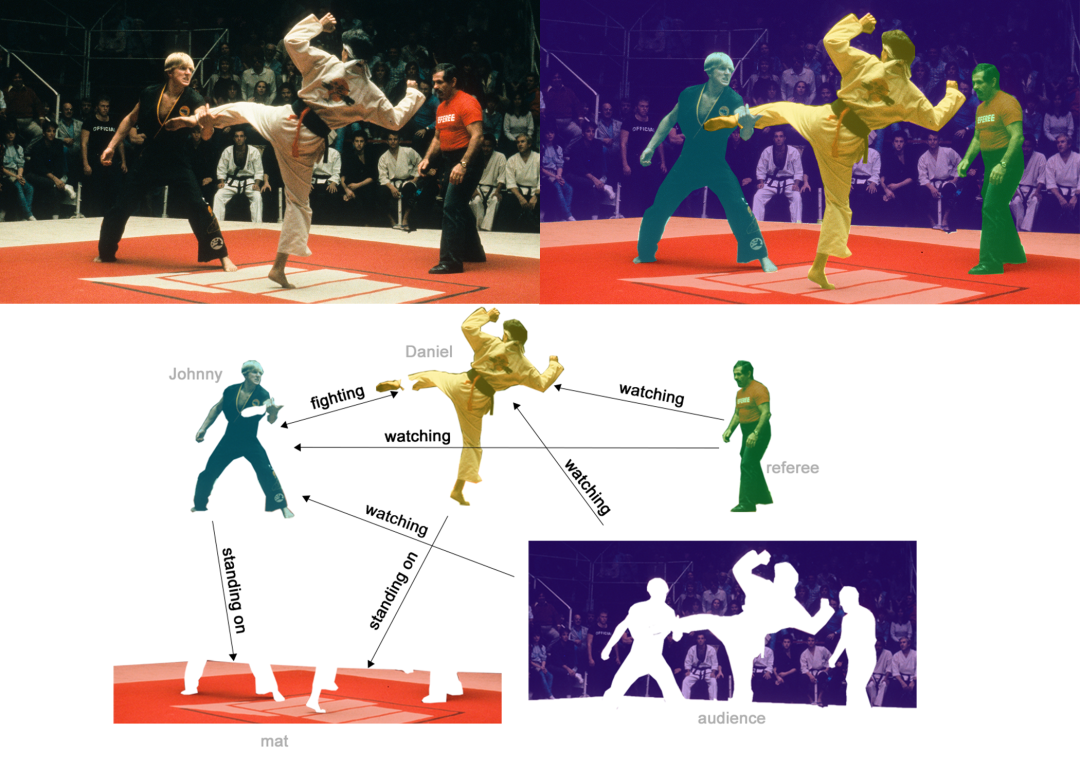
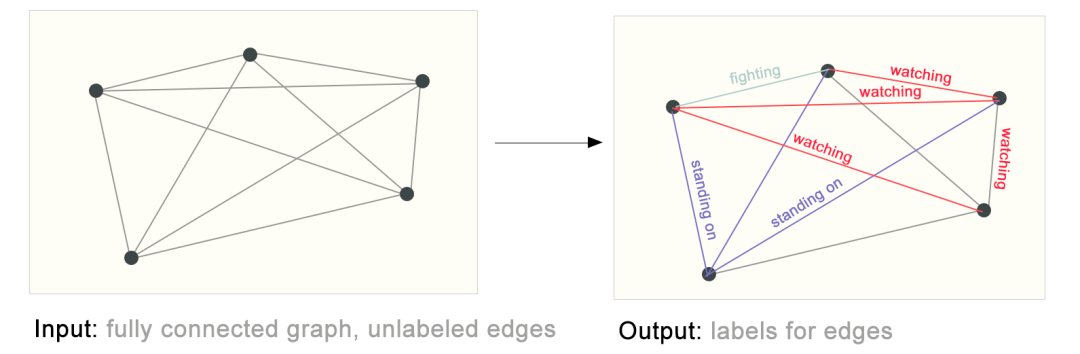
后面我们会看到,这三类任务可以用一个统一的GNN网络解决。
GNN所面对的挑战
前面对于节点,边,图的属性预测GNN都能处理,但对于节点之间的连接性预测却是一种挑战,前面说过用邻接矩阵来表示连接性,当节点数增加,矩阵会变得非常稀疏,内存利用率很低,
例如,下图,仅有四个节点的随机组合对应的邻接矩阵就非常庞大了。
何况更多节点呢?
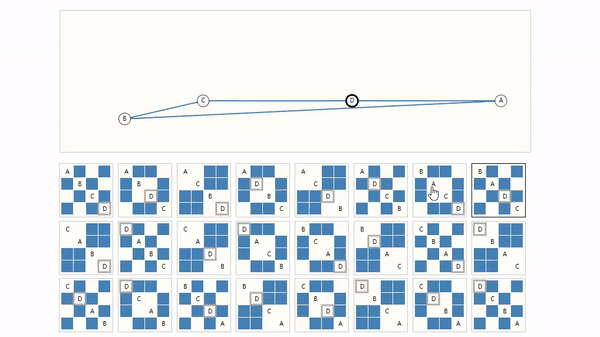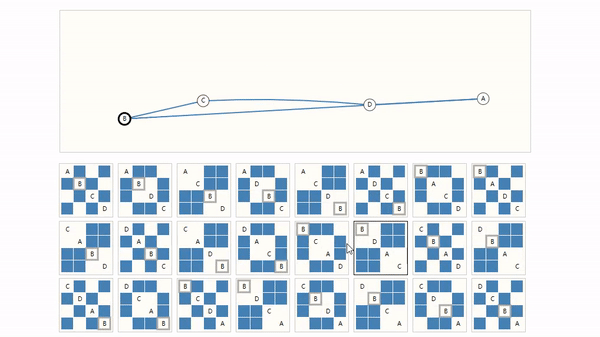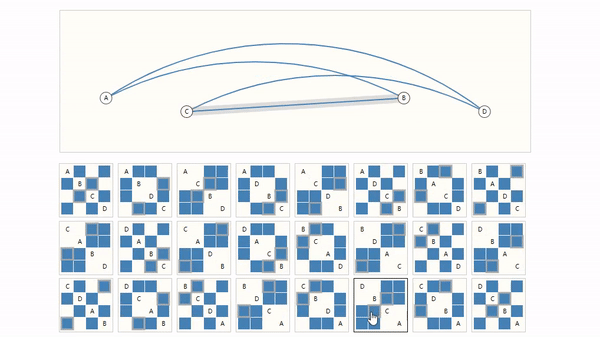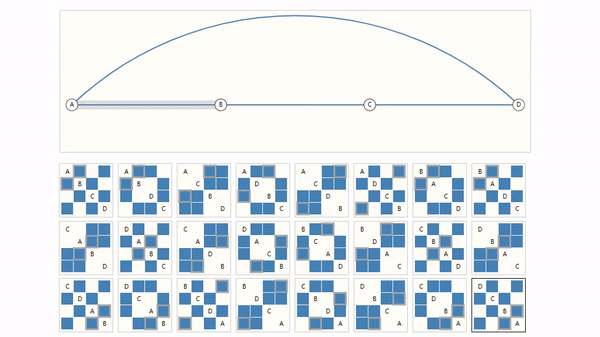
另外,当你将矩阵转置后,GNN输出结果不应该改变,因为转置没有改变节点之间的关系。
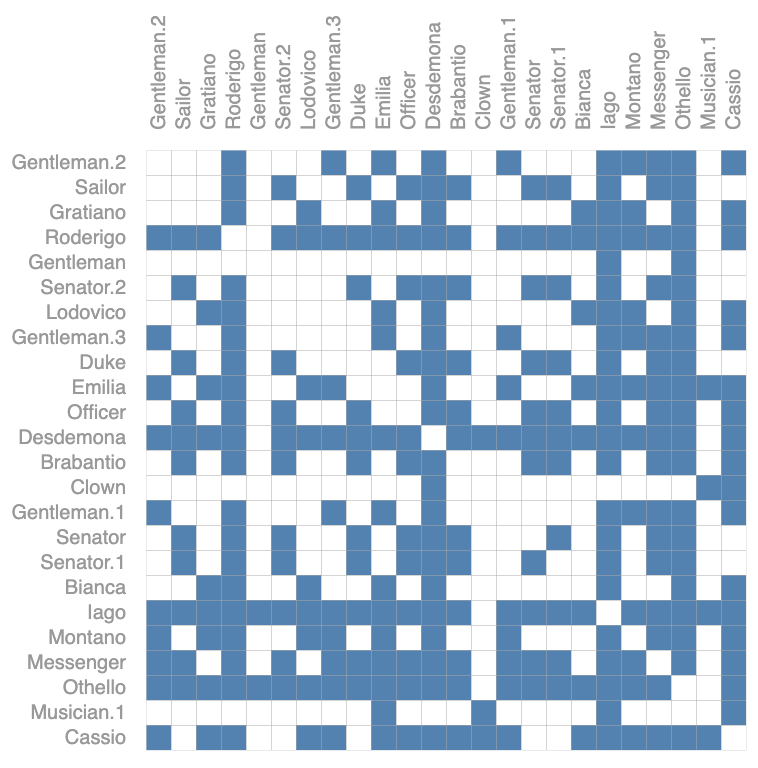
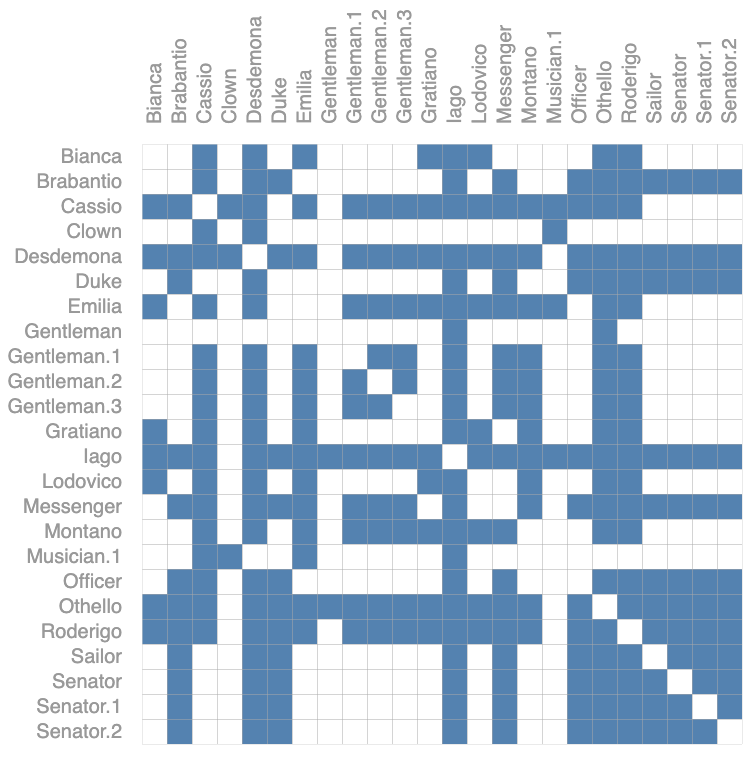
为了解决邻接矩阵带来的挑战,邻接列表应运而生。
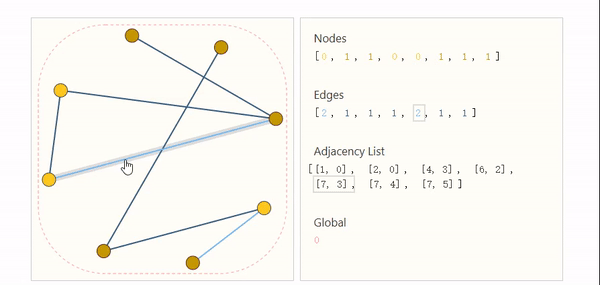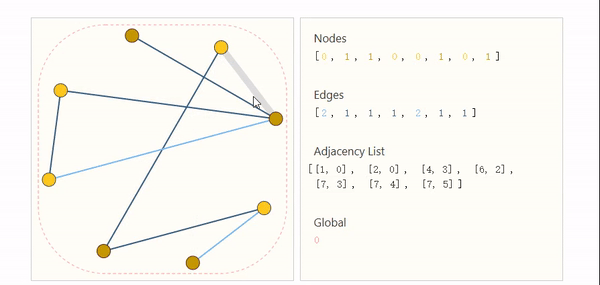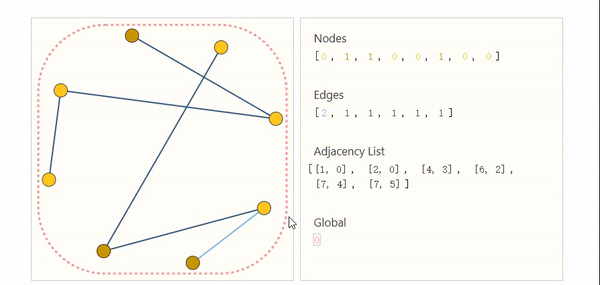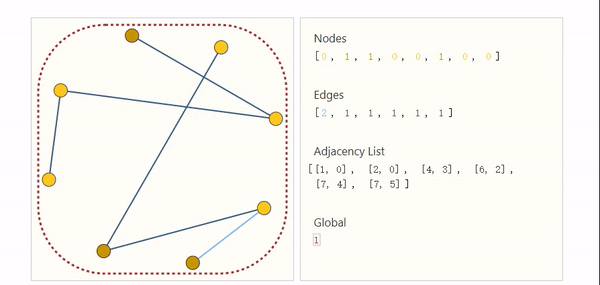
到此我们已经扫清了所有障碍,接下来我们就构建一个简单的分类网络,来看看GNN是如何做预测的?
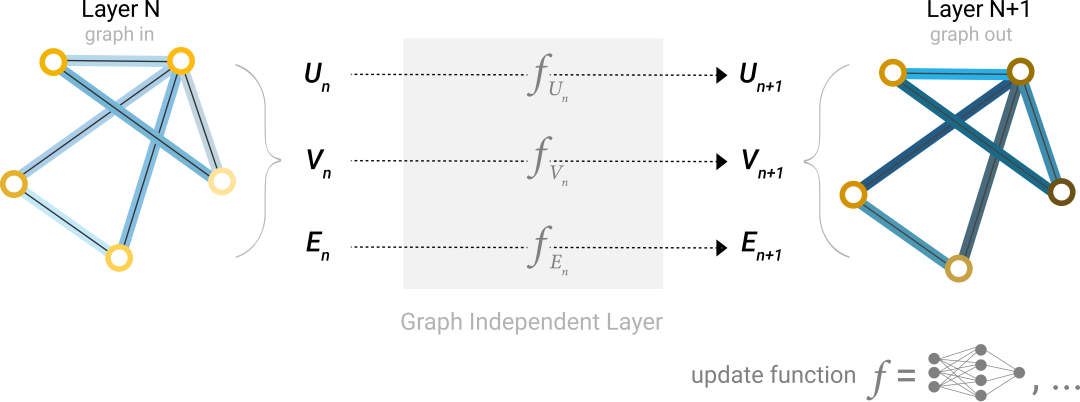
前面我们说过节点,边,图的属性就是一堆向量,也就是前面说的表格数据,处理向量用MLP就可以了,当然你也可以用其他网络,如上图,节点,边,图各有一个MLP,所有点参数共享,也就是所有点共用一个MLP,所有边共用一个MLP。
另外,Layner n+1与上一层相比,图的连接性没变,只改变了属性。也就是可以继续使用初始的邻接链表。
上图构成了一个GNN block,也叫做GNN层,类似CNN中的卷积层,多个GNN 层可以进行累加形成更复杂的网络。
有了GNN block,如果要构建一个节点二分类任务,那么用下面这个网络就够了。
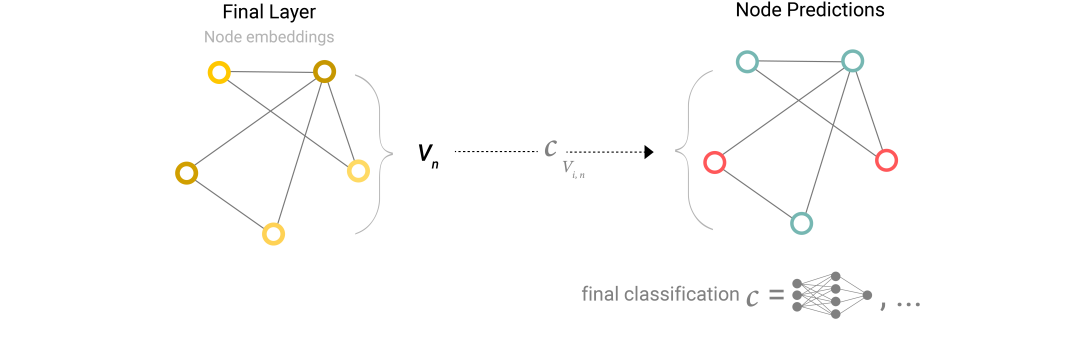
但是,如果一个图只有边有信息,而节点没有存储信息,又要对节点进行分类,该怎么办?
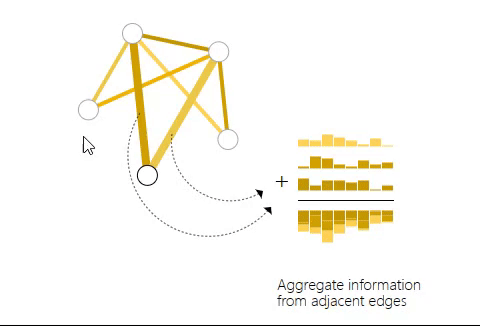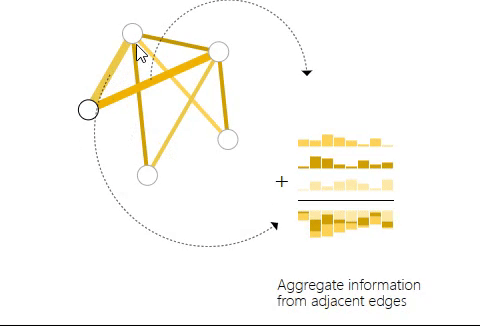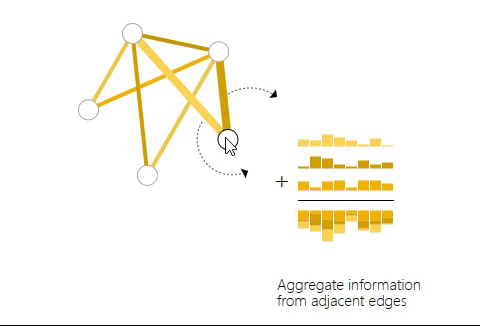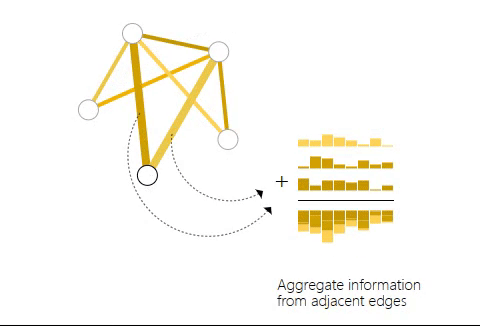
如上图,当对一个节点进行预测时,将所有与其相连的边的信息聚合起来作为节点的属性。
所以,有了信息聚合后,如果只有边的属性,要对节点分类,网络结构如下:
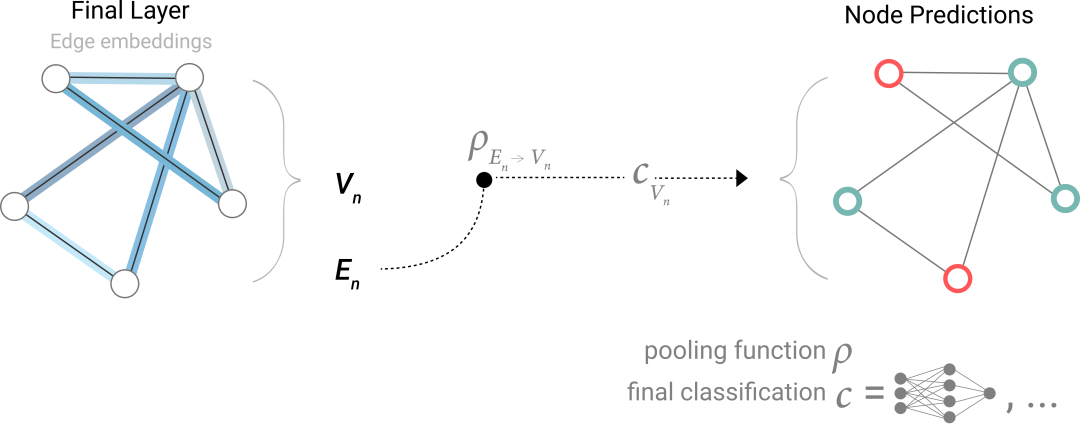
同理,有了信息聚合后,如果只有节点信息,要对边分类,网络结构如下:
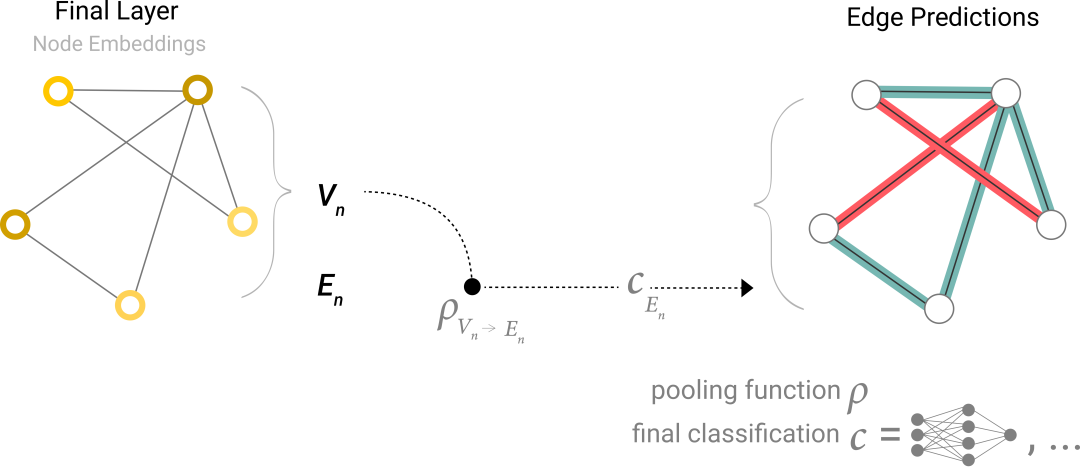
有了信息聚合后,只有节点信息,对图分类:
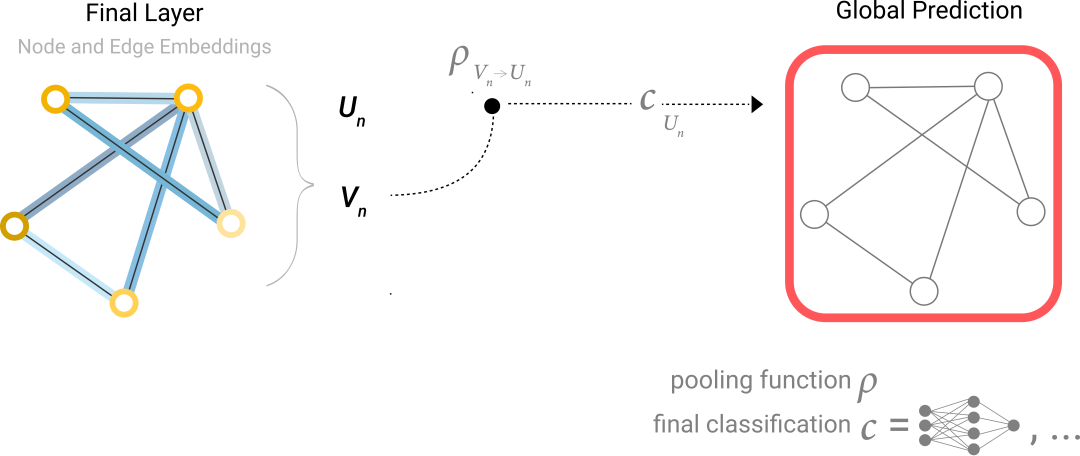
最终的GNN结构如下:
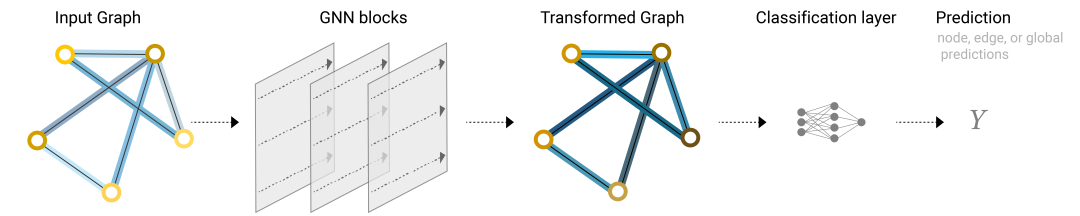
有了信息聚合,就能构建更复杂的GNN网络,这个网络不仅能二分类同样适用于多分类问题。
但是你发现没,上面这个简单的GNN网络并没有利用连接性信息,每个节点以及每条边和全局上下文都是独立处理的。只有在聚合信息进行预测时才使用连接性。
所以,我们可以更进一步的利用聚合信息操作,这样就能进行更复杂的预测。
那么该怎么做呢?
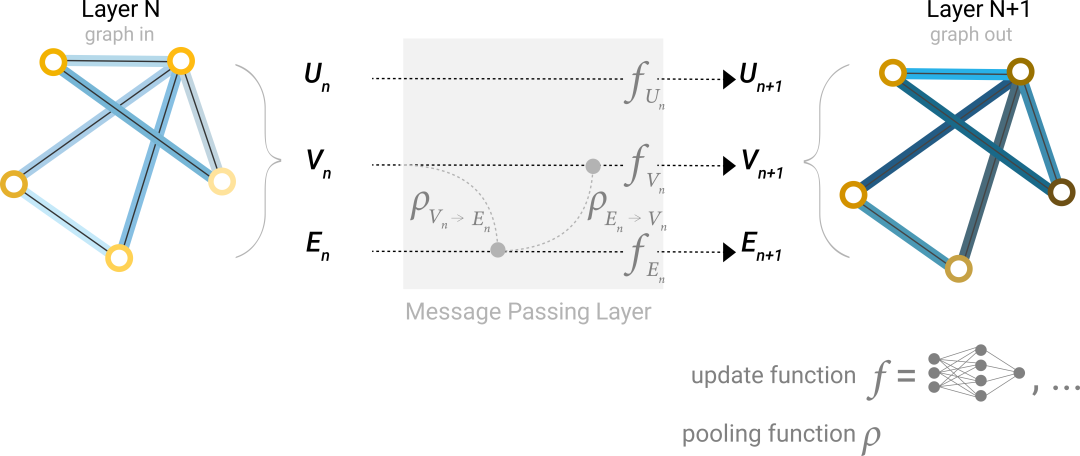
我们可以使用消息传递的方法来实现这一点,即相邻节点或边之间交换信息并影响彼此更新的嵌入。
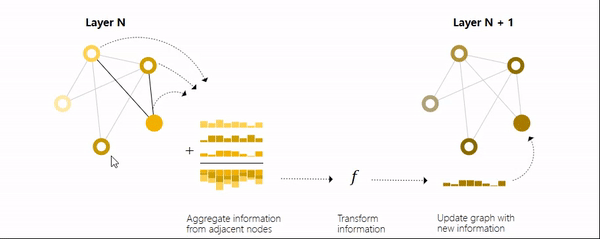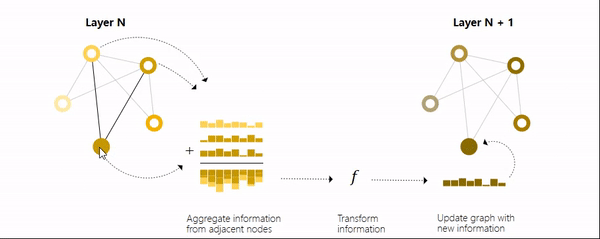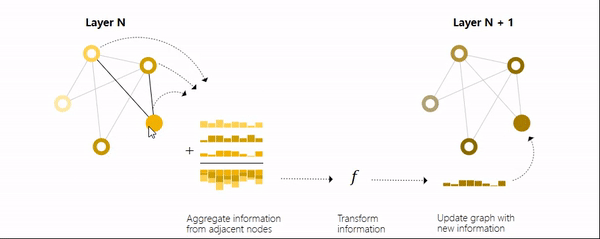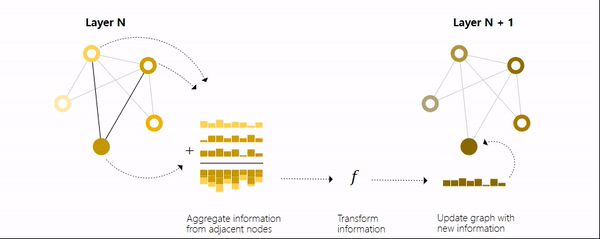
这跟卷积操作有点像,一个特征图的像素对应上一层的一个相邻区域。
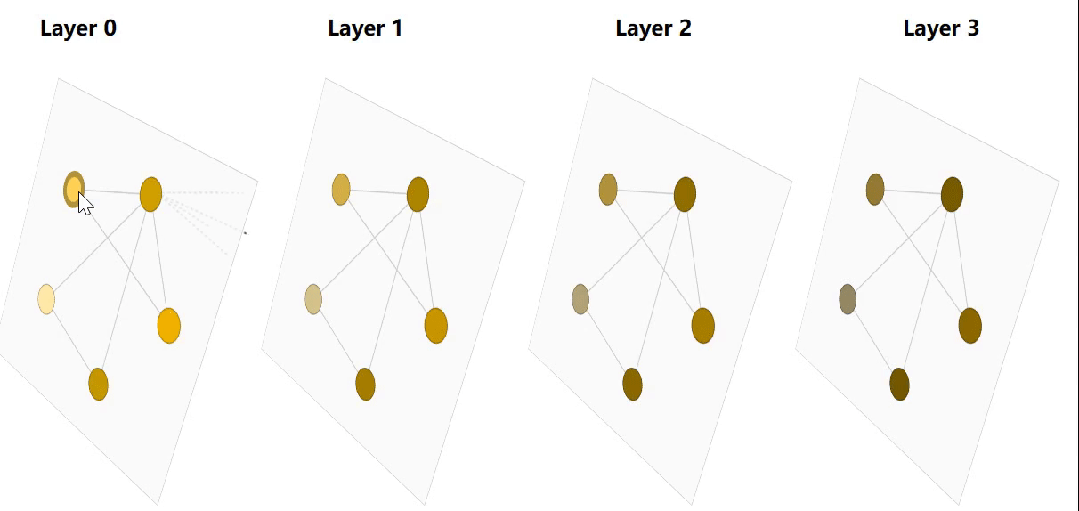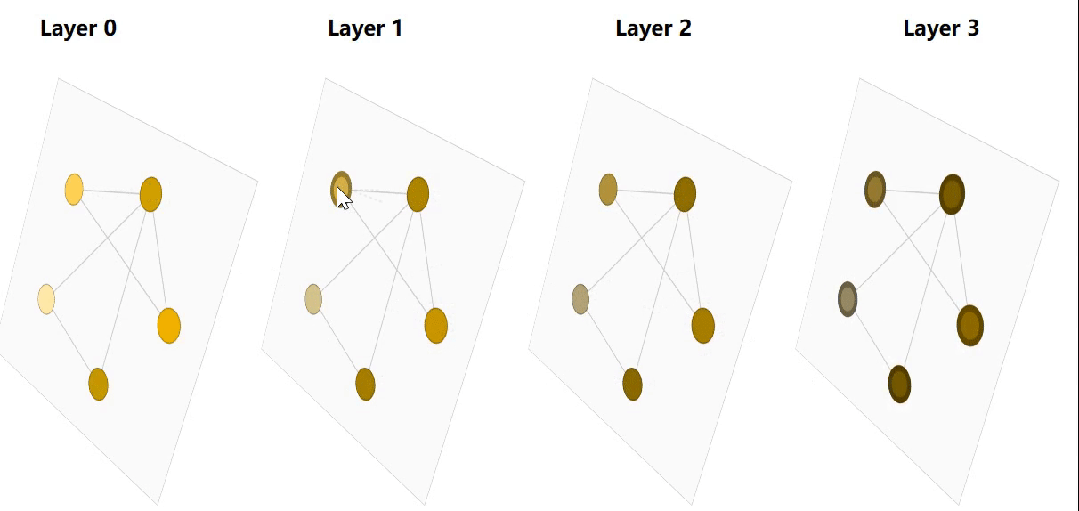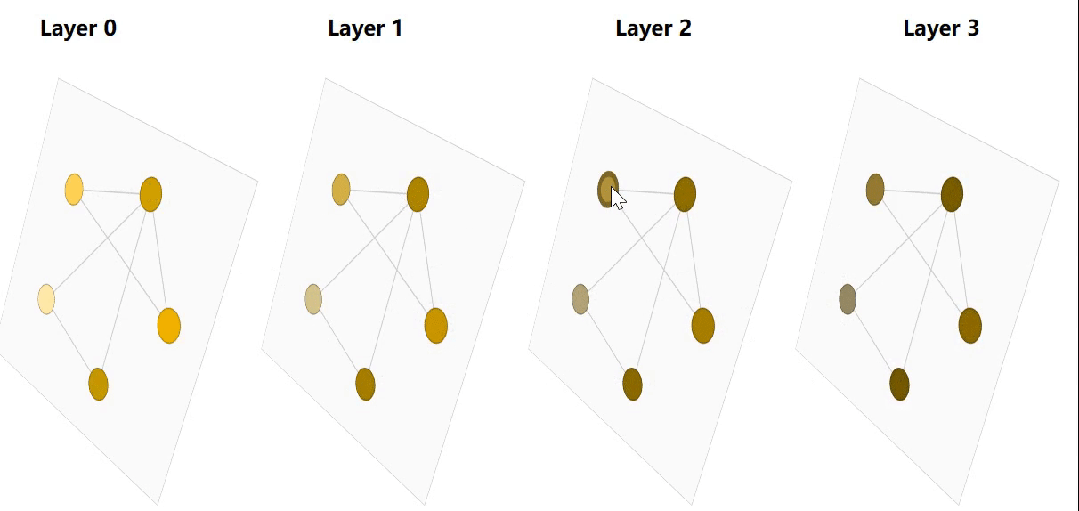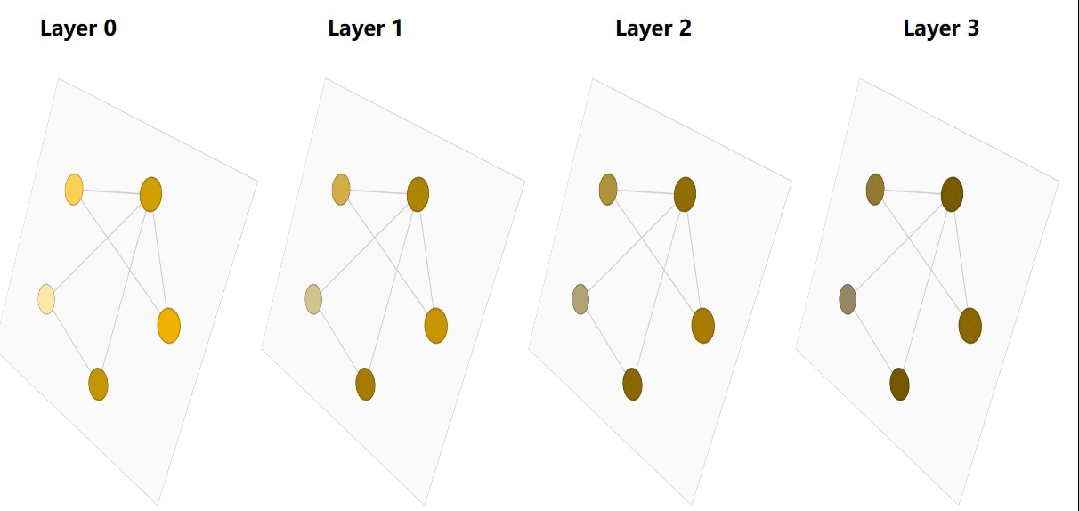
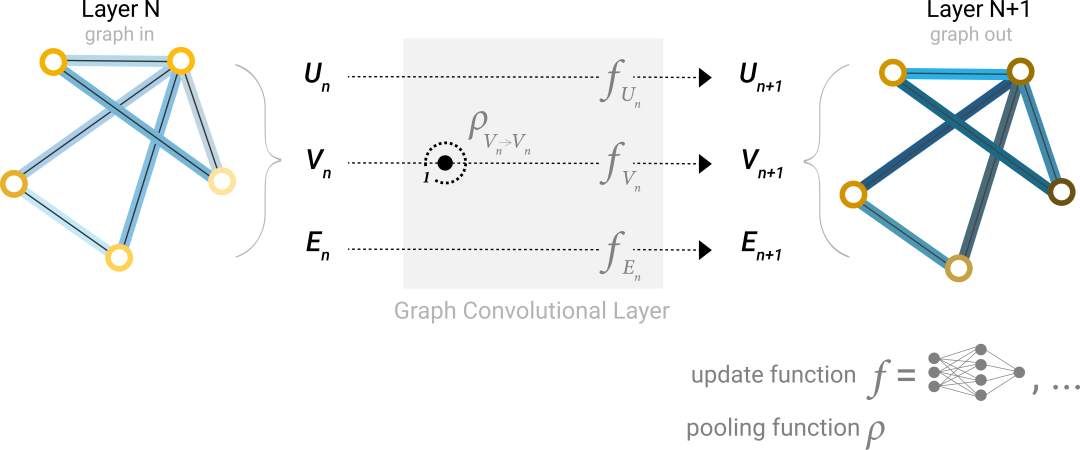
节点层面任务:
边层面任务:
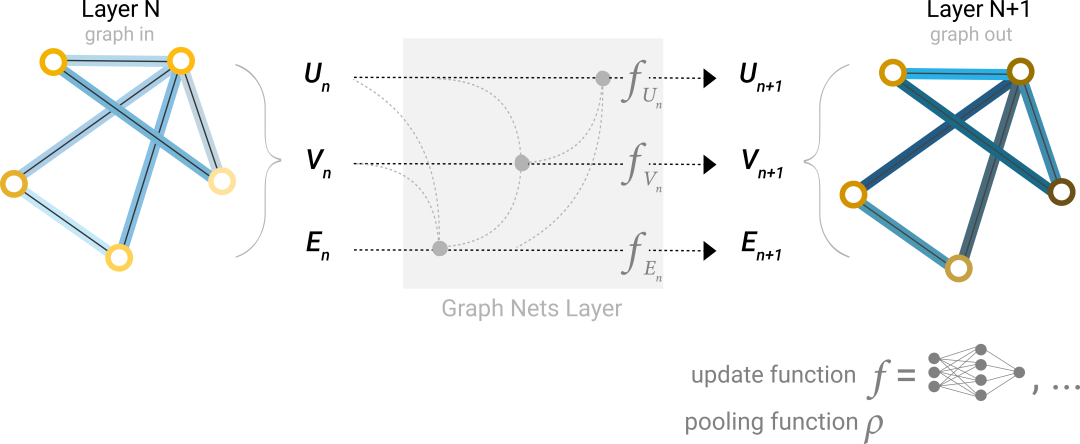
图层面任务:
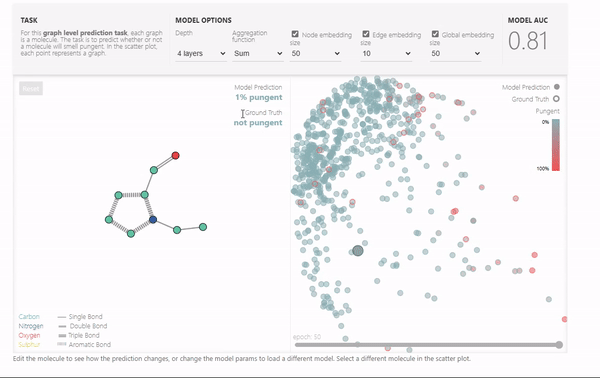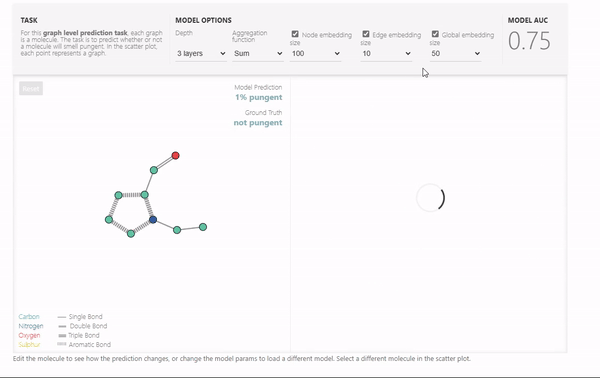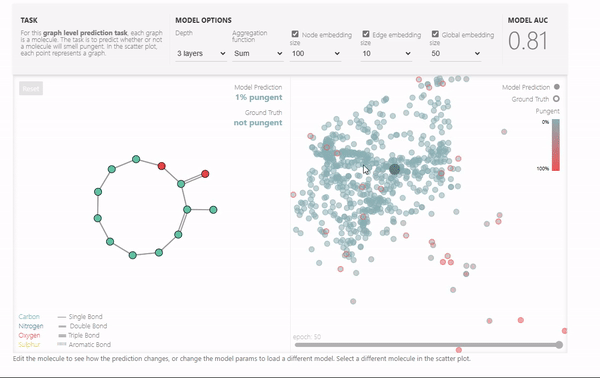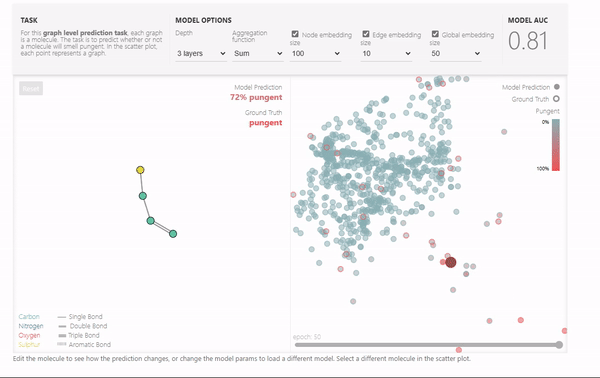
最后,展示了一个Playground,可以改变网络的层数,聚合操作类型,以及各个属性向量的长度,可以通过最终的模型性能来展示各个参数的影响。
原文地址:https://blog.csdn.net/qq_39312146/article/details/134477679
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_5767.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!