当前位置：
  1. 首页
  2. 互联网
  3. 正文
本文介绍: 探索量子物理与计算机科学的交汇点：本文通过一个创新的类比，将量子纠缠与波粒二象性的复杂概念与计算机编程中的指针和函数调用相结合。包含一个简化的Python代码示例，模拟量子对象在观测下表现出波粒二象性的过程，提供了一个直观的方式来理解这些深奥的量子力学现象。虽然仅为概念性的解释，这种独特的视角旨在启发对量子力学基本特性的基础理解。

指向未来: 量子纠缠的本质是一个指针

概述

量子纠缠 (Quantum Entanglement) 是量子系统重两个或多个粒子间的一种特殊连接, 这种连接使得即使相隔很远, 这些粒子的状态也仍然互相依赖.
量子纠缠

基本概念

在探讨量子纠缠之前, 我们先阐述量子比特 (Qubit)的基本概念. 位 (Bit) 是信息的基本单位, 可以处于 0 或 1 的状态. 而量子比特可以同时处于 0 和 1 的叠加态. 即在同时 True 或 False 一个确定的状态, 直到被观测. 量子比特的特性包含叠加和纠缠, 叠加允许量子比特同时存在于多种可能的状态中. 对一个纠缠量子比特的观测会影响与它纠缠的另一个两字比特的状态, 无论两个两字比特相距多远.

理解量子纠缠

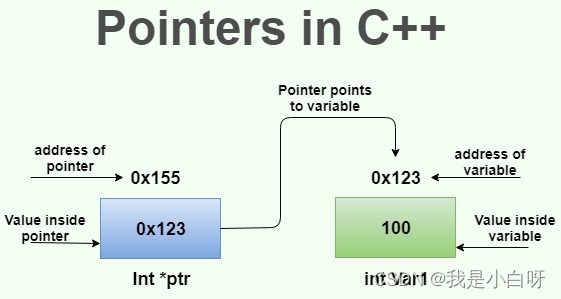
两个变相共享一个指针时, 当一个量子态改变时, 另一个量子态也会随着改变, 不管相隔多远.
在我们所处的 “游戏” 中, 物理空间的限制 (距离) 并不会影响指针, 在我们看来就是类似超光速的方式传递.

指针

Python

class QuantumBit
    def __init__(self, state)
        self.state = state

# 创建量子比特变量
qubit1 = QuantumBit(False)
qubit2 = qubit1

print(id(qubit1), id(qubit2))  # 内存地址相同 (指针)
print(qubit1.state, qubit2.state)  # 调试输出

# 修改量子比特 2 的状态, 1 随着修改
qubit2.state = True
print(qubit1.state, qubit2.state)  # 调试输出

输出结果

1795703080464 1795703080464
False False
True True

Java

public class QuantumBit {
    boolean state;

    public QuantumBit(boolean state) {
        this.state = state;
    }

    public static void main(String[] args) {
        QuantumBit qubit1 = new QuantumBit(false);
        QuantumBit qubit2 = qubit1;

        System.out.println(System.identityHashCode(qubit1) + " " + System.identityHashCode(qubit2));  // 内存地址
        System.out.println(qubit1.state + " " + qubit2.state);  // 调试输出

        // 修改量子比特 2 的状态, 1 随着修改
        qubit2.state = true;
        System.out.println(qubit1.state + " " + qubit2.state);  // 调试输出
    }
}

输出结果:

225534817 225534817
false false
true true

C++

#include <iostream>

class QuantumBit {
    public:
        bool state;

        QuantumBit(bool initState) : state(initState) {}
};

int main() {
    QuantumBit* qubit1 = new QuantumBit(false);
    QuantumBit* qubit2 = qubit1;

    std::cout << qubit1 << " " << qubit2 << std::endl;  // 内存地址
    std::cout << qubit1->state << " " << qubit2->state << std::endl;  // 调试输出

    // 修改量子比特 2 的状态, 1 随着修改
    qubit2->state = true;
    std::cout << qubit1->state << " " << qubit2->state << std::endl;  // 调试输出

    delete qubit1;  // 清理内存
    // 不需要 delete qubit2, 内存地址相同
    return 0;
}

输出结果:

0x54de70 0x54de70
0 0
1 1

理解波粒二象性

同理当我们观测光是粒子还是波的时候, 我们的观测就是在 “游戏” 中调用一次函数, 这就会改变指针的状态, 从而导致量子纠缠的改变或解除 (塌缩).

光既不是粒子也不是波, 拥有绝对速度所以可能呈现为粒子或波, 取决于我们怎么调用函数. 为了避免我们这个 “游戏” 吃过多的算力, 所以没有观测的时候就不需要加载, 观测了才加载.

Python

import random

class QuantumObject:
    def __init__(self):
        # 初始状态为 None，表示既是波也是粒子 (叠加态)
        self.state = None

    def observe(self):
        # 观测时随机决定对象表现为波或粒子
        self.state = random.choice(['wave', 'particle'])
        return self.state

# 创建一个量子对象
quantum_object = QuantumObject()

# 模拟观测过程
for _ in range(10):
    result = quantum_object.observe()
    print(result)

输出结果:

particle
wave
particle
wave
wave
particle
particle
particle
wave
wave

Java

import java.util.Random;

class QuantumObject {
    private String state;

    public QuantumObject() {
        // 初始状态为 null，表示既是波也是粒子 (叠加态)
        this.state = null;
    }

    public String observe() {
        // 观测时随机决定对象表现为波或粒子
        Random random = new Random();
        this.state = random.nextBoolean() ? "wave" : "particle";
        return this.state;
    }
}

public class Main {
    public static void main(String[] args) {
        QuantumObject quantumObject = new QuantumObject();

        // 模拟观测过程
        for (int i = 0; i < 10; i++) {
            String result = quantumObject.observe();
            System.out.println(result);
        }
    }
}

输出结果:

标准输出：particle
wave
particle
particle
wave
wave
wave
particle
wave
wave

C++

#include <iostream>
#include <cstdlib>
#include <ctime>

class QuantumObject {
    std::string state;

public:
    QuantumObject() : state("") {}

    std::string observe() {
        // 观测时随机决定对象表现为波或粒子
        state = (rand() % 2 == 0) ? "wave" : "particle";
        return state;
    }
};

int main() {
    srand(time(0));  // 初始化随机数生成器
    QuantumObject quantumObject;

    // 模拟观测过程
    for (int i = 0; i < 10; i++) {
        std::string result = quantumObject.observe();
        std::cout << result << std::endl;
    }

    return 0;
}

输出结果:

particle
wave
particle
wave
wave
particle
wave
particle
wave
particle

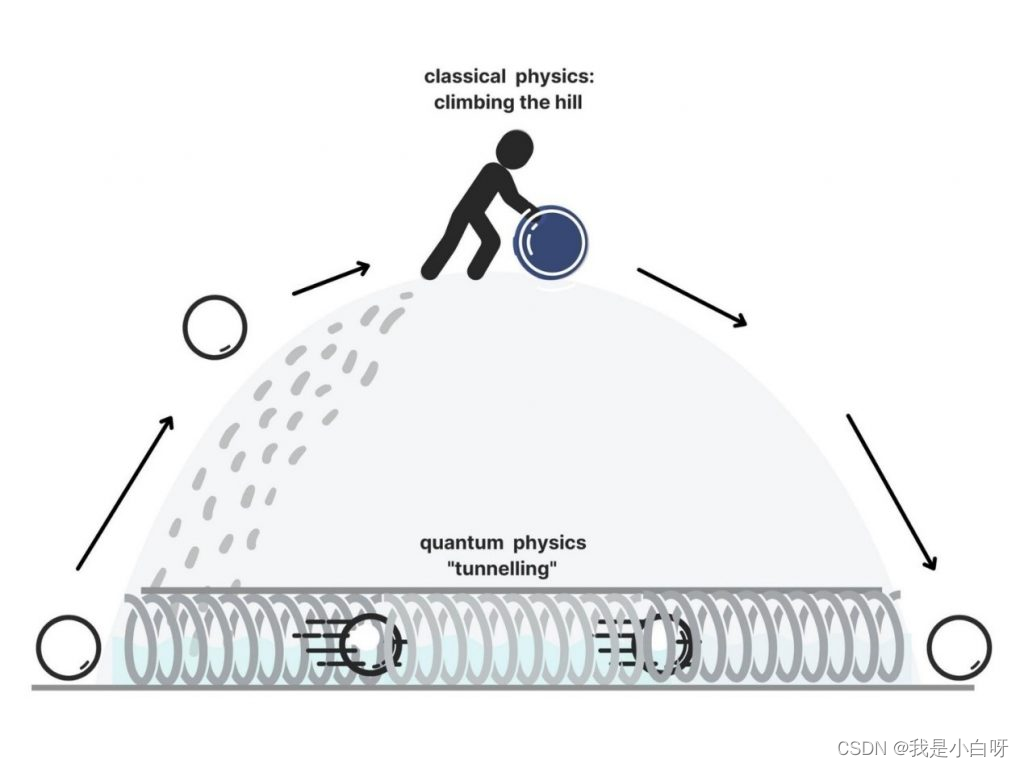
理解量子隧穿

当粒子通过量子势垒时, 正常来说是过不去的. 但是如果粒子是一个函数 (Function), 代表粒子的就是一个函数指针, 量子势垒是一个调度器. 之所以量子无法穿过势垒, 是应该进入势垒后指针发生了偏移. 当我们看到接触势垒被弹回来的粒子, 我们看到的是该粒子的指针, 但是不是原来的例子所指的函数对象了.

量子隧穿

import random

def particle_function():
    return "原始粒子"

def altered_function():
    return "改变后的粒子"

def quantum_barrier(particle):
    if random.random() < 0.5:  # 假设有 50% 概率粒子指针发生偏移
        return altered_function
    else:
        return particle


for _ in range(10):
    # 创建粒子函数指针
    particle_ptr = particle_function

    # 模拟粒子接触量子势垒
    particle_ptr = quantum_barrier(particle_ptr)

    # 输出粒子状态
    print(particle_ptr())

输出结果:

原始粒子
原始粒子
改变后的粒子
改变后的粒子
改变后的粒子
改变后的粒子
改变后的粒子
原始粒子
改变后的粒子
改变后的粒子

理解宇宙常量

为了避免我们这个 “游戏” 产生内存溢出或者消号过多算力, 所以我们需要一些常量 (Constant) 来进行限速.

速度越快时间越慢, 为了避免游戏崩溃, 对于消耗过多算力的函数, 游戏回尽可能少的调用, 放慢时钟. 在物理上就会导师时间间隔变长.

Python

# 光速, 单位: 米 / 秒
SPEED_OF_LIGHT = 299792458

# 普朗克常量, 单位: 焦耳·秒
PLANCK_CONSTANT = 6.62607015e-34

# 万有引力常数, 单位: 牛顿·平方米 / 平方千克
GRAVITATIONAL_CONSTANT = 6.67430e-11

# 玻尔兹曼常量, 单位: 焦耳 / 开尔文
BOLTZMANN_CONSTANT = 1.380649e-23

# 阿伏伽德罗常数, 单位: 1 / 摩尔
AVOGADRO_CONSTANT = 6.02214076e23

# 电子电荷, 单位: 库仑
ELEMENTARY_CHARGE = 1.602176634e-19

# 真空磁导率, 单位: 特斯拉·米 / 安培
VACUUM_PERMEABILITY = 4 * 3.14159265358979323846e-7

# 真空电容率, 单位: 法拉 / 米
VACUUM_PERMITTIVITY = 8.854187817e-12

# 标准大气压, 单位: 帕斯卡
STANDARD_ATMOSPHERE = 101325

# 斯特藩-玻尔兹曼常数, 单位: 瓦特 / 平方米·开尔文^4
STEFAN_BOLTZMANN_CONSTANT = 5.670374419e-8

Java

// 光速, 单位: 米 / 秒
    public static final double SPEED_OF_LIGHT = 299792458;

    // 普朗克常量, 单位: 焦耳·秒
    public static final double PLANCK_CONSTANT = 6.62607015e-34;

    // 万有引力常数, 单位: 牛顿·平方米 / 平方千克
    public static final double GRAVITATIONAL_CONSTANT = 6.67430e-11;

    // 玻尔兹曼常量, 单位: 焦耳 / 开尔文
    public static final double BOLTZMANN_CONSTANT = 1.380649e-23;

    // 阿伏伽德罗常数, 单位: 1 / 摩尔
    public static final double AVOGADRO_CONSTANT = 6.02214076e23;

    // 电子电荷, 单位: 库仑
    public static final double ELEMENTARY_CHARGE = 1.602176634e-19;

    // 真空磁导率, 单位: 特斯拉·米 / 安培
    public static final double VACUUM_PERMEABILITY = 4 * Math.PI * 1e-7;

    // 真空电容率, 单位: 法拉 / 米
    public static final double VACUUM_PERMITTIVITY = 8.854187817e-12;

    // 标准大气压, 单位: 帕斯卡
    public static final int STANDARD_ATMOSPHERE = 101325;

    // 斯特藩-玻尔兹曼常数, 单位: 瓦特 / 平方米·开尔文^4
    public static final double STEFAN_BOLTZMANN_CONSTANT = 5.670374419e-8;

C++

// 阿伏伽德罗常数, 单位: 1 / 摩尔
static constexpr double AVOGADRO_CONSTANT = 6.02214076e23;

// 电子电荷, 单位: 库仑
static constexpr double ELEMENTARY_CHARGE = 1.602176634e-19;

// 真空磁导率, 单位: 特斯拉·米 / 安培
static constexpr double VACUUM_PERMEABILITY = 4 * 3.14159265358979323846e-7;

// 真空电容率, 单位: 法拉 / 米
static constexpr double VACUUM_PERMITTIVITY = 8.854187817e-12;

// 标准大气压, 单位: 帕斯卡
static constexpr int STANDARD_ATMOSPHERE = 101325;

// 斯特藩-玻尔兹曼常数, 单位: 瓦特 / 平方米·开尔文^4
static constexpr double STEFAN_BOLTZMANN_CONSTANT = 5.670374419e-8;

原文地址:https://blog.csdn.net/weixin_46274168/article/details/135640753

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。

如若转载，请注明出处：http://www.7code.cn/show_58082.html

如若内容造成侵权/违法违规/事实不符，请联系代码007邮箱：suwngjj01@126.com进行投诉反馈，一经查实，立即删除！

上一篇 阿里云云原生弹性方案：用弹性解决集群资源利用率难题
下一篇 【音视频】基于NGINX如何播放rtmp视频流

相关文章

发表回复

您的邮箱地址不会被公开。 必填项已用 * 标注

插入图片
浏览器会保存昵称、邮箱和网站cookies信息，下次评论时使用。