本文介绍: 42. 接雨水1 方法一:我的方法2 方法二:动态规划3 方法三:双指针
目录
菜鸟做题第一周,语言是 C++
42. 接雨水
1 方法一:我的方法
Warning:这是我的智障做法,请勿模仿
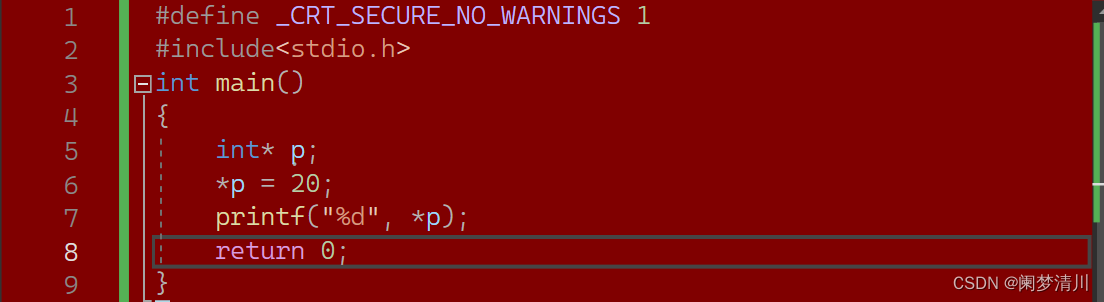
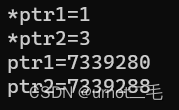
我只能说它教会了我 “&&” 是从左到右进行判断的,第一个不成立就不会看第二个了。当判断条件顺序写反时,即使我写了防止指针越界的约束条件,它也压根看不到。最后就会这样:
解题思路:
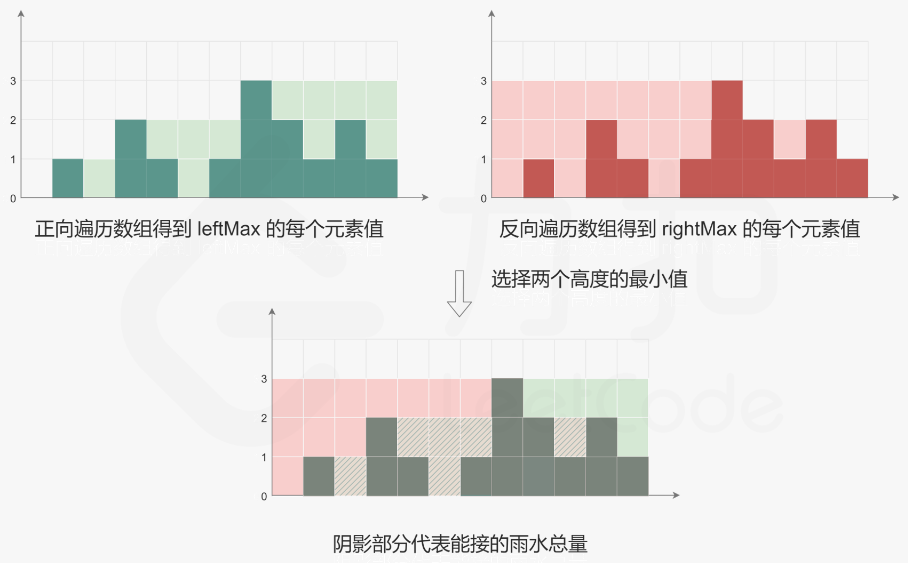
- 正向遍历,算每个下标的积水高度(绿色面积)
- 反向遍历,算每个下标的积水高度(红色面积)
- 取每个下标的积水高度的较小值即为真实积水高度(阴影面积)
力扣官方说明图:
class Solution {
public:
int trap(vector<int>& height) {
int left = 0, right = 0, rain = 0;
unordered_map<int, int> forward, backward;
// 正向遍历
while (left <= height.size() - 1) {
while (right <= height.size() - 1 && height[left] >= height[right])
++right;
if (left + 1 <= height.size() - 1 && height[left] > height[left + 1]) {
int temp = left + 1;
while (temp < right) {
forward[temp] = height[left] - height[temp];
++temp;
}
left = right - 1;
}
++left;
}
// 反向遍历
left = height.size() - 1, right = height.size() - 1;
while (right >= 0) {
while (left > 0 && height[left] <= height[right])
--left;
if (right - 1 >= 0 && height[right] > height[right - 1]) {
int temp = right - 1;
while (temp > left) {
backward[temp] = height[right] - height[temp];
--temp;
}
right = left + 1;
}
--right;
}
// 计算雨水
for (int i = 0; i < height.size() - 1; ++i) {
rain += min(forward[i], backward[i]);
}
return rain;
}
};2 方法二:动态规划
解题思路:
- 正向遍历,算每个区域的局部最大高度(绿色)
- 反向遍历,算每个区域的局部最大高度(红色)
- 取每个下标的最大高度的较小值再减该下标的高度
- 总和为 rain 积水量
事实证明是我没有彻底理解官方题解的思路,所以才搞出了方法一这种智障解法。
力扣官方说明图:

class Solution {
public:
int trap(vector<int>& height) {
int n = height.size();
vector<int> leftMax(n), rightMax(n);
if (n == 0) return 0;
// 正向遍历
leftMax[0] = height[0];
for (int i = 1; i < n; ++i) {
leftMax[i] = max(leftMax[i - 1], height[i]);
}
// 反向遍历
rightMax[n - 1] = height[n - 1];
for (int i = n - 2; i >= 0; --i) {
rightMax[i] = max(rightMax[i + 1], height[i]);
}
// 计算雨水
int rain = 0;
for (int i = 0; i < n; ++i) {
rain += min(leftMax[i], rightMax[i]) - height[i];
}
return rain;
}
};3 方法三:双指针
思路说明:
方法二是完成正向遍历和反向遍历后才来计算 rain 积水量,而方法三是利用双指针一左一右同时开始遍历,并且可以直接计算 rain 积水量。
由于每次移动前都立即计算了:
leftMax = max(leftMax, height[left]);
rightMax = max(rightMax, height[right]);所以下面的两个不等式成立:
- 若 height[left] < height[right],则必有 leftMax < rightMax
- 若 height[left] > height[right],则必有 leftMax > rightMax
那么就可以直接计算 rain 积水量了:
- 若 height[left] < height[right],则 rain += leftMax – height[left]
- 若 height[left] > height[right],则 rain += rightMax – height[right]
一开始我觉得很难理解,但是动动笔写一下,就知道不等式成立了。比如,对于第一个不等式,就可能存在 height[left] < leftMax < rightMax < height[right] 或者 leftMax < height[left] < rightMax < height[right] 等情形,它们都会使不等式成立。
class Solution {
public:
int trap(vector<int>& height) {
int n = height.size(), rain = 0;
if (n == 0) return 0;
int leftMax = 0, rightMax = 0;
int left = 0, right = n - 1;
while (left != right) {
leftMax = max(leftMax, height[left]);
rightMax = max(rightMax, height[right]);
if (height[left] < height[right]) {
rain += leftMax - height[left];
++left;
} else {
rain += rightMax - height[right];
--right;
}
}
return rain;
}
};原文地址:https://blog.csdn.net/m0_64140451/article/details/135707651
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_59380.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!
主题授权提示:请在后台主题设置-主题授权-激活主题的正版授权,授权购买:RiTheme官网
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。