【数学建模】图论模型

图的基础理论及networkx简介

图的基本概念

1. 无向图和有向图
2. 简单图和完全图：重边、环、孤立点
3. 赋权图/网络
4. 顶点的度
5. 子图与生成子图
6. 路与回路、迹、path、圈
7. 连通图与非连通图

图的表示及Networkx简介

图的表示

考虑简单图

1. 关联矩阵表示
   

2. 邻接矩阵表示
   
   对于赋权图而言，邻接矩阵中的数值改为对应边的权值就得到对应的无向/有向赋权图

NetworkX简介

python语言
图论与复杂网络建模工具
内置常用图与复杂网络分析算法

绘图布局
图形布局共五种

1. circular_layout：顶点在一个圆环上均匀分布；
2. random_layout：顶点随机分布；
3. shell_layout：顶点在同心圆上分布；
4. spring_layout： 用Fruchterman-Reingold算法排列顶点；
5. spectral_layout：根据图的拉普拉斯特征向量排列顶点

最短路算法及其Python实现

Dijkstra（迪克斯特拉）标号算法和Floyd（弗洛伊德）算法
Dijkstra标号算法只适用于边权是非负的情形
最短路问题也可以归结为一个0-1整数规划模型

固定起点到其余各点的最短路算法

Dijkstra（迪克斯特拉）标号算法
赋权图

G

(

V

,

E

,

W

)

G(V,E,W)

G(V,E,W)，其中顶点集

V

=

{

v

1

,

.

.

.

,

v

n

}

V={v_1, …, v_n}

V={v1​,…,vn​}， 边集

E

E

E，邻接矩阵

W

=

(

w

i

j

)

n

x

n

W=(w_{ij})_{n x n}

W=(wij​)nxn​，且

w

i

j

w_{ij}

wij​满足

记号确定

d

(

u

0

,

v

0

)

d(u_0, v_0)

d(u0​,v0​) ：顶点

u

0

u_0

u0​到顶点

v

0

v_0

v0​的最短距离

l

(

v

)

l(v)

l(v)：起点

u

0

u_0

u0​到

v

v

v的当前路长度

z

(

v

)

z(v)

z(v)：顶点

v

v

v的父顶点标号

S

i

S_i

Si​：具有永久标号的顶点集

每对顶点间的最短路算法

Floyd（弗洛伊德）算法
动态规划算法，递推产生矩阵序列

A

1

,

A

2

,

.

.

.

,

A

k

,

.

.

.

,

A

n

A_1, A_2, …, A_k, …, A_n

A1​,A2​,…,Ak​,…,An​，矩阵

A

k

=

(

a

k

(

i

,

j

)

)

n

x

n

A_k=(a_k(i,j))nxn

Ak​=(ak​(i,j))nxn，第

i

i

i行第

j

j

j列元素

a

k

(

i

,

j

)

a_k(i,j)

ak​(i,j)表示从顶点

v

i

v_i

vi​到顶点

v

j

v_j

vj​路径上顶点数不大于

k

k

k的最短路径长度
迭代公式

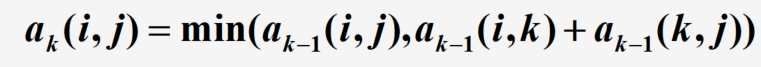
networkx求所有顶点对之间最短路径的函数为
shortest_path(G, source=None, target=None, weight=None, method='dijkstra')，返回值是可迭代类型，其中method可以取值dijkstra，bellman-ford

最短路应用

设备更新问题


转化为最短路问题
赋权有向图

D

=

(

V

,

A

,

W

)

D=(V, A, W)

D=(V,A,W)，顶点集

V

=

{

v

1

,

v

2

,

.

.

.

,

v

5

}

V={v_1, v_2, …, v_5}

V={v1​,v2​,…,v5​}，

v

i

v_i

vi​（

i

=

1

,

2

,

3

,

4

i=1, 2, 3, 4

i=1,2,3,4）表示第

i

i

i年年初，

v

5

v_5

v5​表示第4年年末，A为边集，W为邻接矩阵，

w

i

j

w_{ij}

wij​为第

i

i

i年年初到第

j

j

j年年初/第

j

−

1

j-1

j−1年年末所支付的费用，计算公式为

w

i

j

=

p

i

+

∑

i

j

−

1

a

k

−

r

j

w_{ij} = p_i+sum_i^{j-1}a_k-r_j

wij​=pi​+i∑j−1​ak​−rj​
说明：

p

i

p_i

pi​为第

i

i

i年年初机器的购置费用，

a

k

a_k

ak​为第

k

k

k年的机器维护费用，

r

i

r_i

ri​为第

i

i

i年末机器的出售价格
根据这个公式计算得到邻接矩阵

W

W

W，并且原问题转化为求解

v

1

v_1

v1​到

v

5

v_5

v5​的费用最短路

结果

重心问题/选址问题

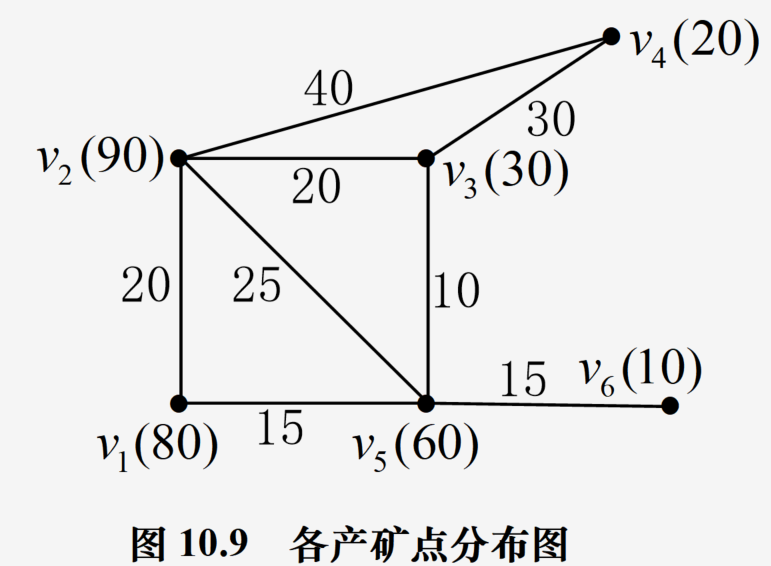
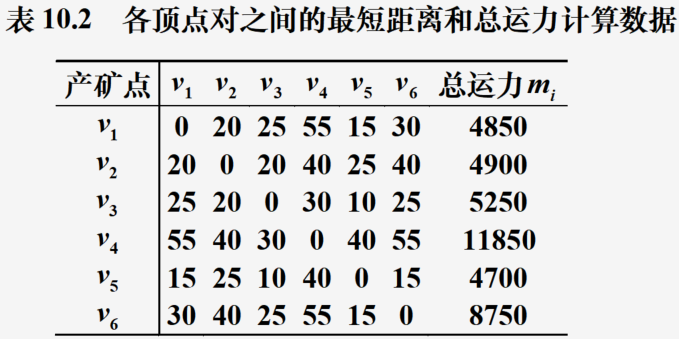
问题转化：求出各个顶点对之间的最短距离，然后得到某一顶点到其他各个顶点的（最短重量·距离）和最小，这个顶点即为所求

计算结果展示

最小生成树算法及其networkx实现

基本概念

1. 树：连通的五圈图
2. 树的判定定理：n个顶点m条边的图
3. 生成树、最小生成树

最小生成树算法

Kruskal算法和Prim算法
Kruskal算法
贪心，每次选择权值最小的边加入子图T，并保证不形成环，直到子图中包含

n

−

1

n-1

n−1条边为止
Prim算法
使用两个集合

P

P

P和

Q

Q

Q，从任意

p

∈

P

p in P

p∈P，

v

∈

V

−

P

v in V-P

v∈V−P，选择最小权值的边

p

v

pv

pv，将

v

v

v加入

P

P

P，

p

v

pv

pv加入Q，直到

P

=

V

P=V

P=V为止
说明：对比Kruskal算法和Prim算法，Kruskal算法是显式地说明了不能在生成子图中出现环，Prim算法则是通过设定选定新边的一个顶点在

P

P

P集合，一个顶点在

V

−

P

V-P

V−P集合这样隐式保证的

NetworkX提供接口
T=minimum_spanning_tree(G, weight='weight', algorithm='kruskal')
G为输入图
algorithm的取值有三种字符串：‘kruskal’，‘prim’，或’boruvka’，缺省值为’kruskal’
返回值T为所求得的最小生成树的可迭代对象

示例

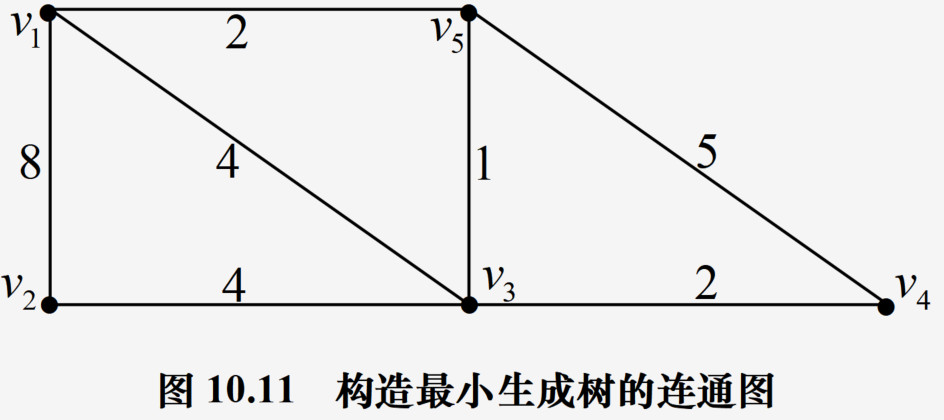
最小生成树应用

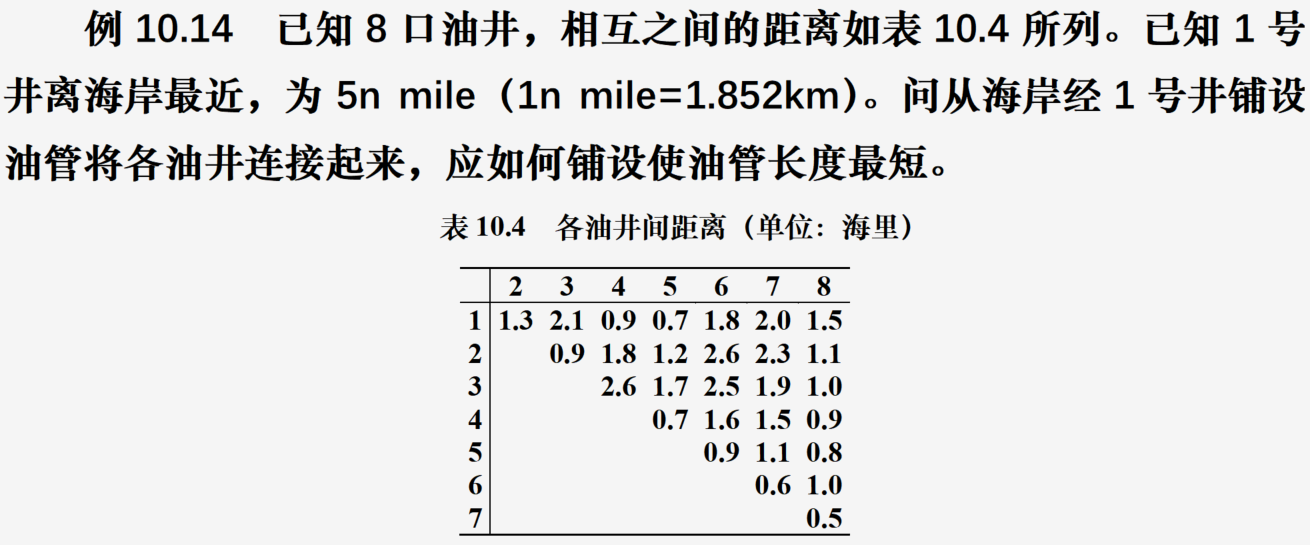
说明：从这个题看出最小生成树和最短路算法的区别，最短路在找的是各个节点到某个节点的最短，而最小生成树在找的是一条通过全部节点的最短路

结果

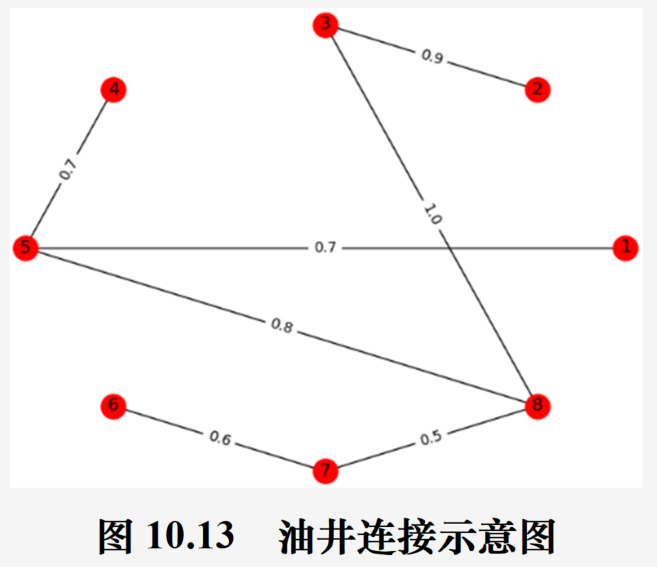
匹配问题

问题转化：赋权图

G

=

(

V

,

E

,

W

^

)

G=(V, E, hat{W})

G=(V,E,W^) ，顶点集

V

=

{

v

1

,

v

2

,

.

.

.

,

v

10

}

V={v_1, v_2, …, v_{10}}

V={v1​,v2​,…,v10​}，

v

1

,

v

2

,

.

.

.

,

v

5

v_1, v_2, …, v_5

v1​,v2​,…,v5​表示5个人，

v

6

,

v

7

,

v

8

,

v

9

,

v

10

v_6, v_7, v_8, v_9, v_{10}

v6​,v7​,v8​,v9​,v10​表示5项工作，邻接矩阵

W

^

hat{W}

W^满足

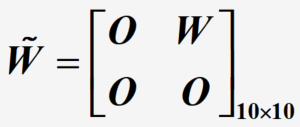
代码：

import numpy as np
import networkx as nx
from networkx.algorithms.matching import max_weight_matching
a=np.array([[3,5,5,4,1],[2,2,0,2,2],[2,4,4,1,0],
            [0,2,2,1,0],[1,2,1,3,3]])
b=np.zeros((10,10)); b[0:5,5:]=a; G=nx.Graph(b)
#返回值为（人员，工作）的集合
s0=max_weight_matching(G)  
s=[sorted(w) for w in s0]
L1=[x[0] for x in s]; L1=np.array(L1)+1  #人员编号
L2=[x[1] for x in s]; L2=np.array(L2)-4  #工作编号
c=a[L1-1,L2-1]  #提取对应的效益
d=c.sum()  #计算总的效益
print("工作分配对应关系为：n人员编号：",L1)
print("工作编号：", L2); print("总的效益为：",d)

最大流最小费用问题

网络流问题——如何安排使流量最大，即最大流问题，如公路系统中有车辆流、物资调配系统中有物资流、金融系统中有现金流等

基本概念

1. 有向图$D(V,A)$
2. 可行流的条件
3. 增广路

最大流问题可写为这样一个线性规划问题

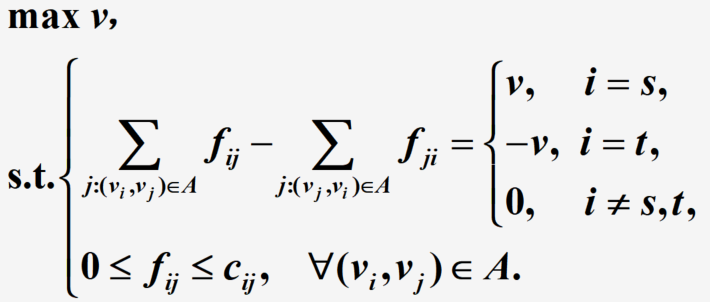
Ford-Fulkerson算法寻求最大流

使用NetworkX求解网络最大流

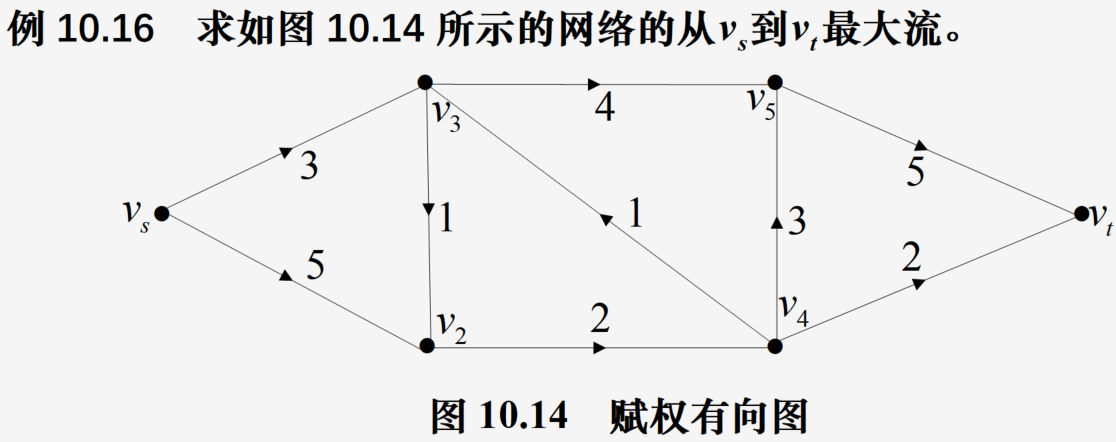
最小费用流问题

标号说明

f

i

j

f_{ij}

fij​为弧

(

v

i

,

v

j

)

(v_i, v_j)

(vi​,vj​)上的流量，

b

i

j

b_{ij}

bij​为弧

(

v

i

,

v

j

)

(v_i, v_j)

(vi​,vj​)上的单位费用，

c

i

j

c_{ij}

cij​为弧

(

v

i

,

v

j

)

(v_i, v_j)

(vi​,vj​)上的容量，问题转化为下面的线性规划问题

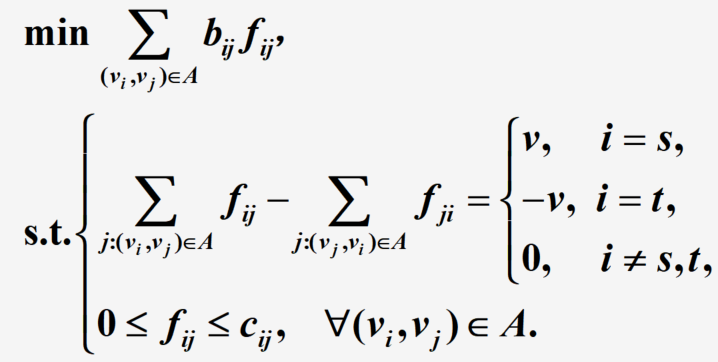
当

v

=

v

m

a

x

v=v_{max}

v=vmax​时，问题有解；当

v

>

v

m

a

x

v > v_{max}

v>vmax​时，问题无解

使用NetworkX求解问题

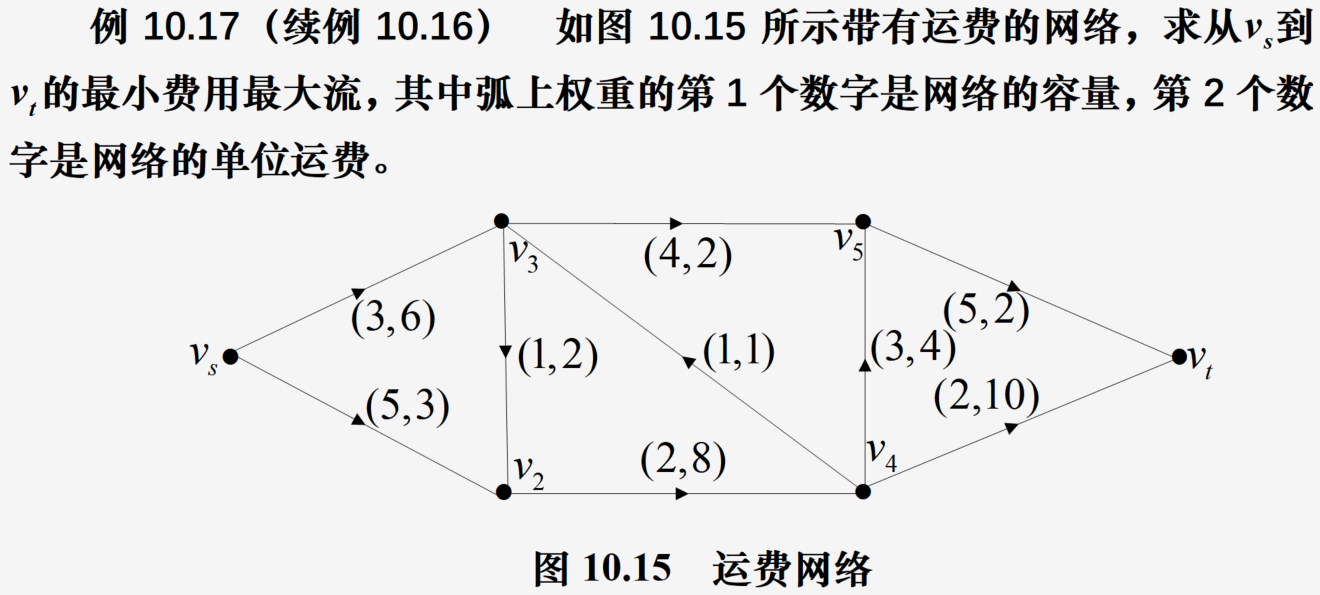
代码：

import numpy as np
import networkx as nx
L=[(1,2,5,3),(1,3,3,6),(2,4,2,8),(3,2,1,2),(3,5,4,2),
   (4,3,1,1),(4,5,3,4),(4,6,2,10),(5,6,5,2)]
G=nx.DiGraph()
for k in range(len(L)):
    G.add_edge(L[k][0]-1,L[k][1]-1, capacity=L[k][2], weight=L[k][3])
mincostFlow=nx.max_flow_min_cost(G,0,5)
print("所求流为：",mincostFlow)
mincost=nx.cost_of_flow(G, mincostFlow)
print("最小费用为：", mincost)
flow_mat=np.zeros((6,6),dtype=int)
for i,adj in mincostFlow.items():
    for j,f in adj.items():
        flow_mat[i,j]=f
print("最小费用最大流的邻接矩阵为：n",flow_mat)

PageRank算法

引文分析思想
当网页甲有一个链接指向网页乙，就认为乙获得了甲对它贡献的分值，该值的多少取决于网页甲本身的重要程度，即网页甲的重要性越大，网页乙获得的贡献值就越高。
由于网络中网页链接的相互指向，pagerank分值计算为一个迭代过程，最终网页根据所得分值进行排序

假设
我们在上网时浏览页面并选择下一个页面的过程，与过去浏览过哪些页面无关，而仅依赖于当前所在的页面。
这一选择过程可以认为是一个有限状态、离散时间的随机过程，其状态转移规律用Markov链描述

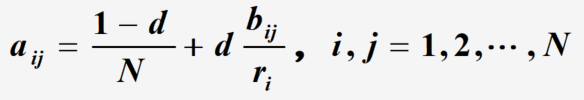
说明：

a

i

j

a_{ij}

aij​表示从页面

i

i

i转移到页面

j

j

j的概率，

1

−

d

N

frac{1-d}{N}

N1−d​为随机跳转时到页面

j

j

j的概率，

d

b

i

j

r

i

d frac{b_{ij}}{r_i}

dri​bij​​为根据连接进行跳转到页面

j

j

j的概率

再根据正则Markov的平稳分布，得到各个网页被访问的概率分布，这个概率就被定义为各个网页的PageRank值

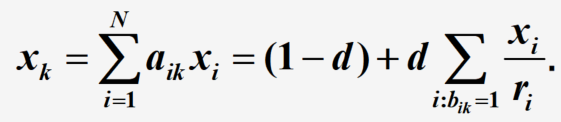
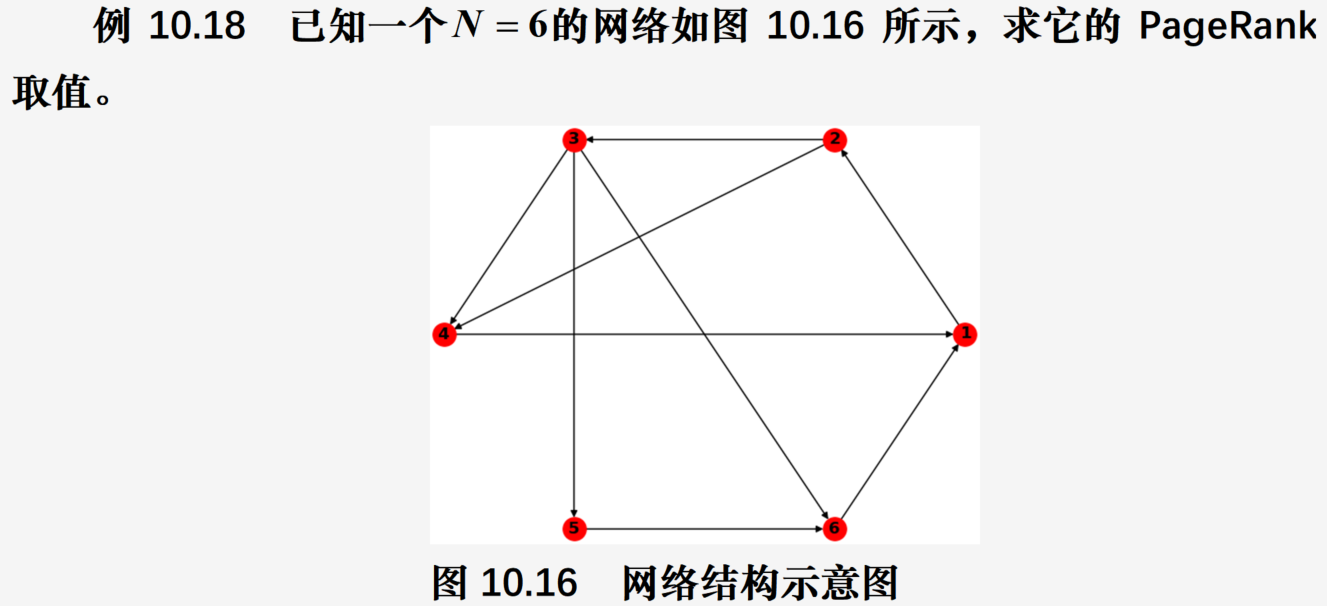
使用NetworkX求解

复杂网络简介

重点关注复杂网络的统计性质，并使用NetworkX计算

复杂网络概况

复杂网络：具有自组织、自相似、吸引子、小世界、无标度中部分或全部性质的网络
特征：结构复杂、网络进化、连接多样性、动力学复杂性、节点多样性
研究内容：网络的几何性质，网络的形成机制，网络演化的统计规律，网络上的模型性质，以及网络的结构稳定性，网络的演化动力学机制等问题
基本测度：度（degree）及其分布特征，度的相关性，集聚程度及其分布特征，最短距离及其分布特征，介数(betweenness)及其分布特征，连通集团的规模分布

1. 节点的度和度分布：度分布一般用直方图展示，$A^2$
2. 平均路径长度，网络直径
3. 聚类系数

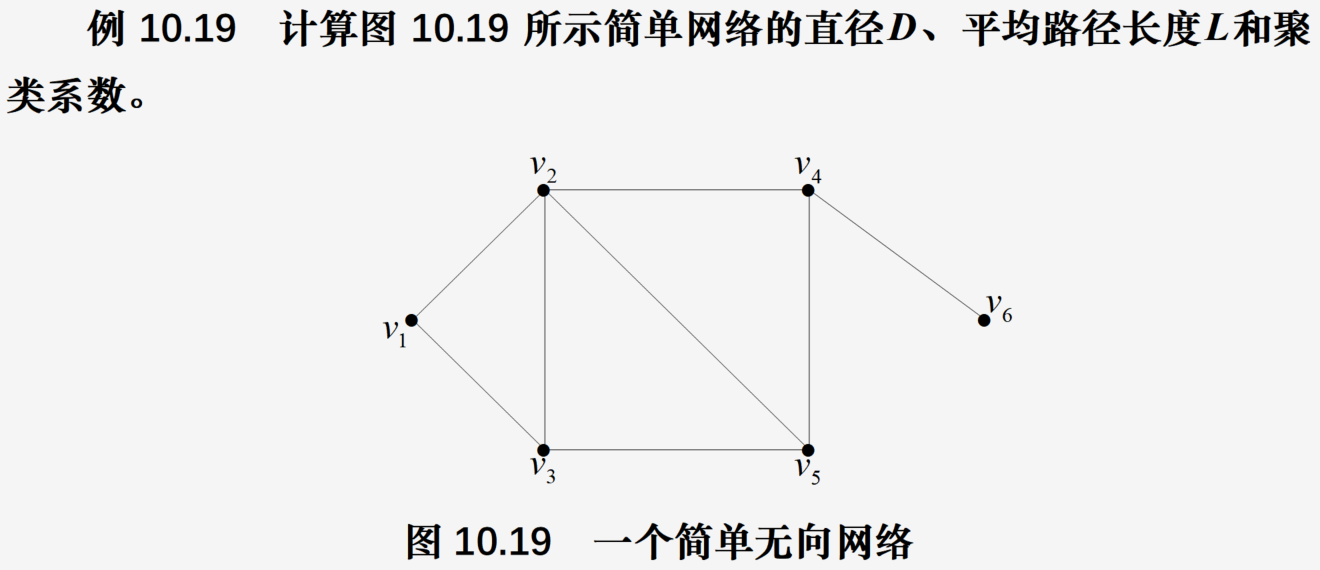
代码：

import numpy as np
import networkx as nx
L=[(1,2),(1,3),(2,3),(2,4),(2,5),(3,5),
   (4,5),(4,6)]
G=nx.Graph()   #构造无向图
G.add_nodes_from(range(1,7))  #添加顶点集
G.add_edges_from(L)
D=nx.diameter(G)  #求网络直径
LH=nx.average_shortest_path_length(G) #求平均路径长度
Ci=nx.clustering(G)   #求各顶点的聚类系数
C=nx.average_clustering(G)  #求整个网络的聚类系数
print("网络直径为：",D,"n平均路径长度为：",LH)
print("各顶点的聚类系数为：")
for index,value in enumerate(Ci.values()):
    print("(顶点v{:d}: {:.4f})；".format(index+1,value),end=' ')
print("n整个网络的聚类系数为：{:.4f}".format(C))