树的一些经典 Oj题讲解

本文介绍: 树的OJ题讲解

关于树的遍历

先序遍历

我们知道树的遍历有前序遍历中序遍历后序遍历然后我们如果用递归的方式去解决，对我们来说应该是轻而易举的吧！那我们今天要讲用迭代（非递归）实现树的相关遍历
首先呢我们得知道迭代解法本质上也是在模拟递归，因为递归的过程中使用了系统栈，所以我们在迭代的时候也要用Stack来模拟系统栈。
我们要一开始就要创建一个顺序表接收打印的值最终程序结束输出出来。
首先我们要创建一个栈来存放结点，首先我们就要打印根节点的值，此时栈中的内容为null，所以我们优先将头结点puth进去栈，然后打印。其实就很好理解如果树为空直接就返回了。

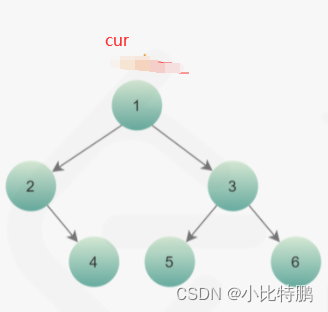
在这里插入图片描述
我们首先从根节点开始遍历只要节点不为空就进入循环就push 进栈再打印再去遍历左子树，直到左子树为空，就进不来循环了我们就要从栈中弹出元素，去遍历他的右子树但是现在只有一层循环不能够继续进入回到上面再进入左子树的循环那怎么办呢我们就可以再加一层循环在最外面包着他们判断条件依然是节点不为空，但是这样就解决了吗当然还没有你去遍历右子树肯定会最后右孩子结点为空又怎么返回循环呢此时已经节点为空了进不去循环了但是还没遍历结束，该怎么办呢现在栈还没空也是一个判断条件我们就可以再外层循环加一个条件栈不为空。

最终的实现你们可以参考代码：

public List<Integer> preorderTraversal(TreeNode root) {
        //先定义一个顺序表去接收
        List<Integer> list = new ArrayList<>();
        if(root == null){
            return list;
        }

        //用链表去实现一个栈
        Deque<TreeNode> stack = new LinkedList<TreeNode>();
        TreeNode cur = root;
        while(cur != null || !stack.isEmpty()){
        while(cur != null){
            list.add(cur.val);
            stack.push(cur);
            cur = cur.left;
        }
        cur = stack.pop();
        cur = cur.right;
        }
        return list;
    }

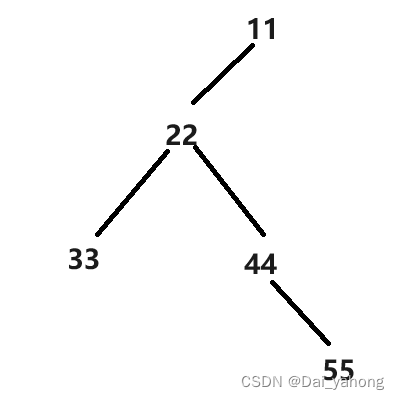
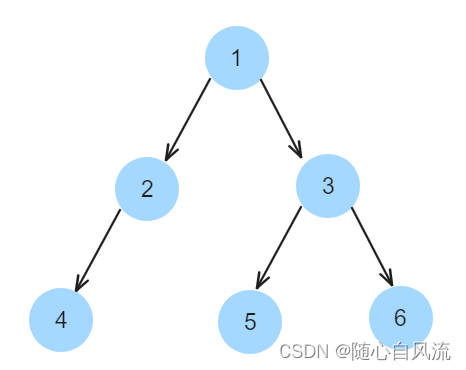
根据代码去分析上面那棵二叉树我们就可以输出他的二叉树遍历序列。

中序遍历

通过上面的先序遍历，我们可以知道大概的思路。其实中序遍历迭代（非递归）实现和先序遍历的实现其实差不太多就输出的位置换一下因为是 左根右 ，所以我们先去遍历完左子树，push进栈。左子树为空的时候再从栈中弹出元素打印元素。
具体代码实现如下：

 public List<Integer> inorderTraversal(TreeNode root) {
 //先定义一个顺序表去接收
        List<Integer> list = new ArrayList<>();
        if(root == null){
            return list;
        }

        //用链表去实现一个栈
        Deque<TreeNode> stack = new LinkedList<TreeNode>();
        TreeNode cur = root;
        while(cur != null || !stack.isEmpty()){
        while(cur != null){
            
            stack.push(cur);
            cur = cur.left;
        }
        cur = stack.pop();
        list.add(cur.val);
        cur = cur.right;
        }
        return list;
    }

写到这里大家是不是觉得 so easy 后序遍历想直接开敲，但是这里提醒大家后序遍历没有前序和中序那样简单了后序会涉及到一个记录结点。下面我们来分析一下

后序遍历

大体思路和前面两种一样还是利用栈来实现因为后序遍历是 左右根。
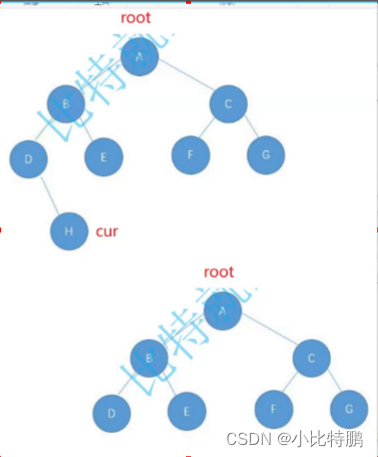
在这里插入图片描述
首先我们先用cur遍历左子树，只要左子树不为空，就push进栈如果左子树为空的话怎么办呢？我们要从栈中弹出元素吗那肯定不行啊因为你还得判断后面有没有右子树，所以你只能peek出来看一下。如果有右子树我们则让cur = peek出来的节点的右子树，如果右子树为空呢我们是不是可以pop出栈并且打印出来。然后现在cur是为空的进不去循环然后我们又peek一下栈顶元素判断他右子树为不为空但是你会发现现在代码死循环了他还是会打印刚才的打印过的节点的值那怎么办呢？很简单我们定义一个节点prev 来记录一下打印过的结点。只要peek出来的元素的右孩子是prev 说明打印过就直接将他弹出来打印所以现在我们有两个条件可以直接弹出来打印然后记录一下，就是当右孩子为空或者右孩子是已经打印过的结点就可以弹出栈顶的元素打印因为该元素已经是最后一次用了。
下面我们直接上代码：

 public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        if(root == null){
            return list;
        }
        //创建一个栈
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        TreeNode prev = null;//用来记录打印过的结点
        while(cur != null || !stack.isEmpty()){
            while(cur != null){
                stack.push(cur);
                cur = cur.left;
            }
            //只能拿出来看一下 不能弹出来
            TreeNode top = stack.peek();
            if(top.right == null ||top.right == prev ){ 
    //这里代码会出现死循环  因为会一直在那个结点 所以我们要记录的节点 加一个判断条件
                stack.pop();
                list.add(top.val);
                prev = top;
            }else{
                cur = top.right;
            }
        }
        return list;
    }

二叉树转字符串

题目是这样描述的给你二叉树的根节点 root ，请你采用前序遍历的方式，将二叉树转化为一个由括号和整数组成的字符串，返回构造成的字符串。

空节点用一对空括号“（）”表示，转化后可以省略所有不影响字符串与原始的二叉树直接的一对一关系的空括号对。

相信大家读完题目会觉得很懵，其实题目的情况分为4种：
1.左右子树都有则需要这样加括号：root((left),(right));
2、只有右子树：root((), (right));
3、只有左子树：root((right));
4、叶子节点：root；

总的来说不管有没有左子树，只要有右子树左子树都要加括号。
下面来看几个示例：
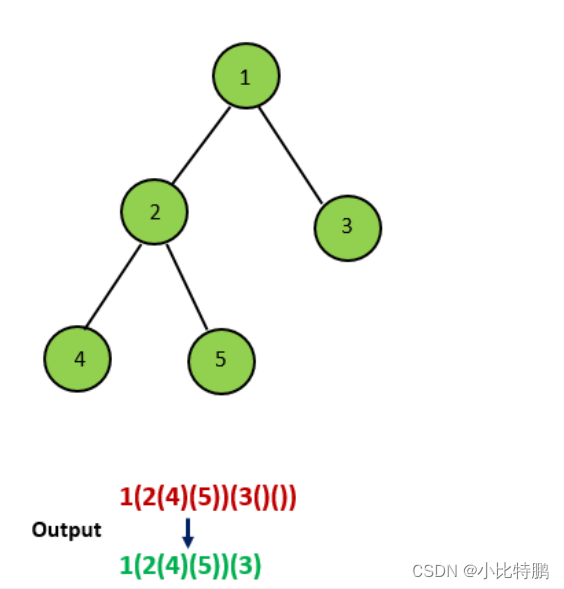
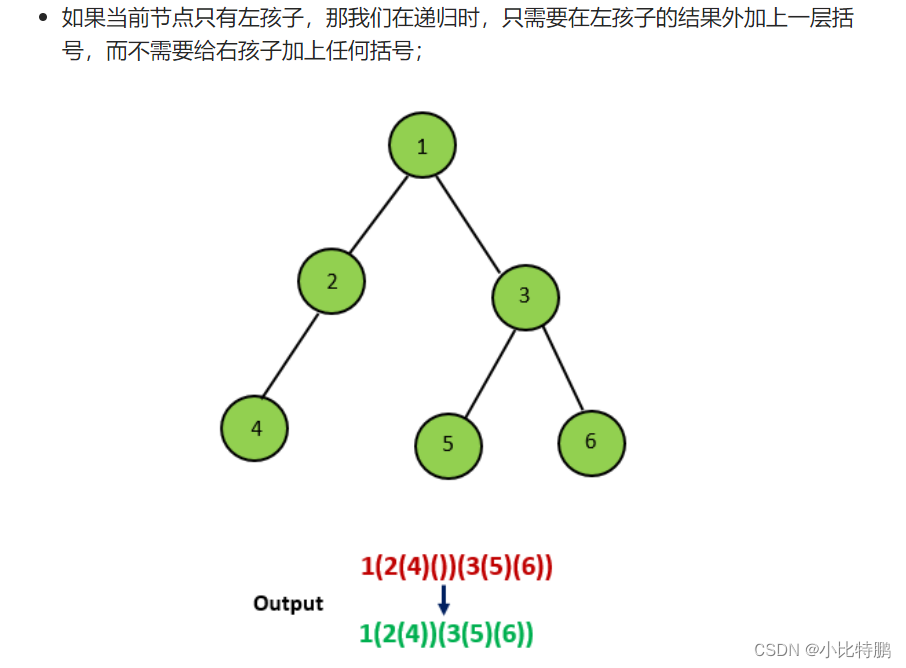
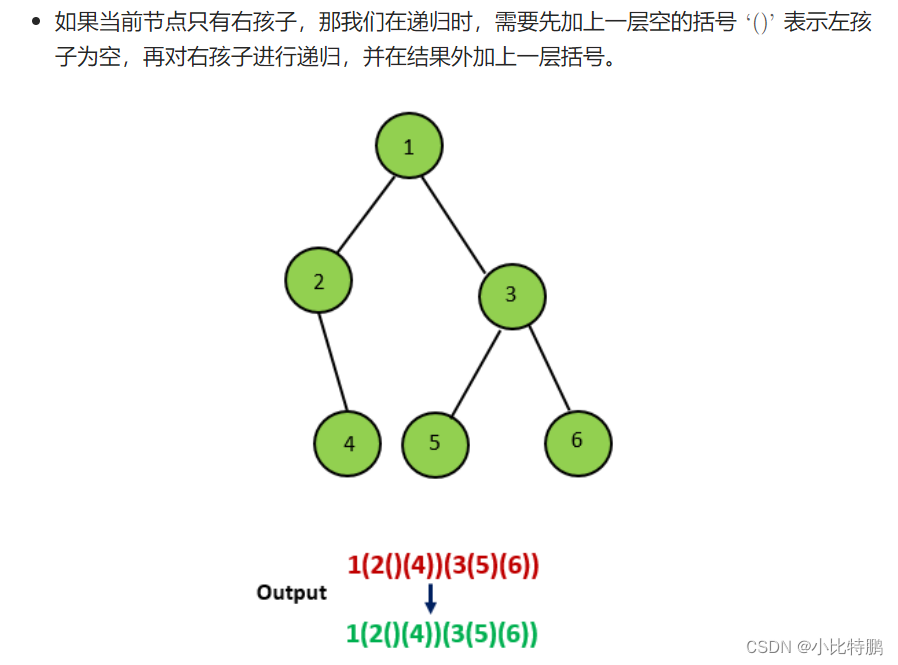
在这里插入图片描述

看完示例相信大家已经知道思路了我们直接上代码：

 StringBuilder sb = new StringBuilder();
    public String tree2str(TreeNode root) {
        preoderTraveral(root);
        return sb.toString();
    }
    private void preoderTraveral(TreeNode root){
        if(root == null){
            return;
        }
        sb.append(root.val);
        if(root.left != null || root.right != null){
            sb.append("(");
            preoderTraveral(root.left);
            sb.append(")");
            if(root.right != null){
                sb.append("(");
                preoderTraveral(root.right);
                sb.append(")");
            }
        }
    }