647.回文子串 516.最长回文子序列

本文介绍: 给定一个字符串，你的任务是计算这个字符串中有多少个回文子串。具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。提示：输入的字符串长度不会超过 1000。

647.回文子串 516.最长回文子序列

647.回文子串

力扣题目链接(opens new window)

给定一个字符串，你的任务是计算这个字符串中有多少个回文子串。

具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。

示例 1：

输入：“abc”
输出：3
解释：三个回文子串: “a”, “b”, “c”

示例 2：

输入：“aaa”
输出：6
解释：6个回文子串: “a”, “a”, “a”, “aa”, “aa”, “aaa”

提示：输入的字符串长度不会超过 1000 。

思路

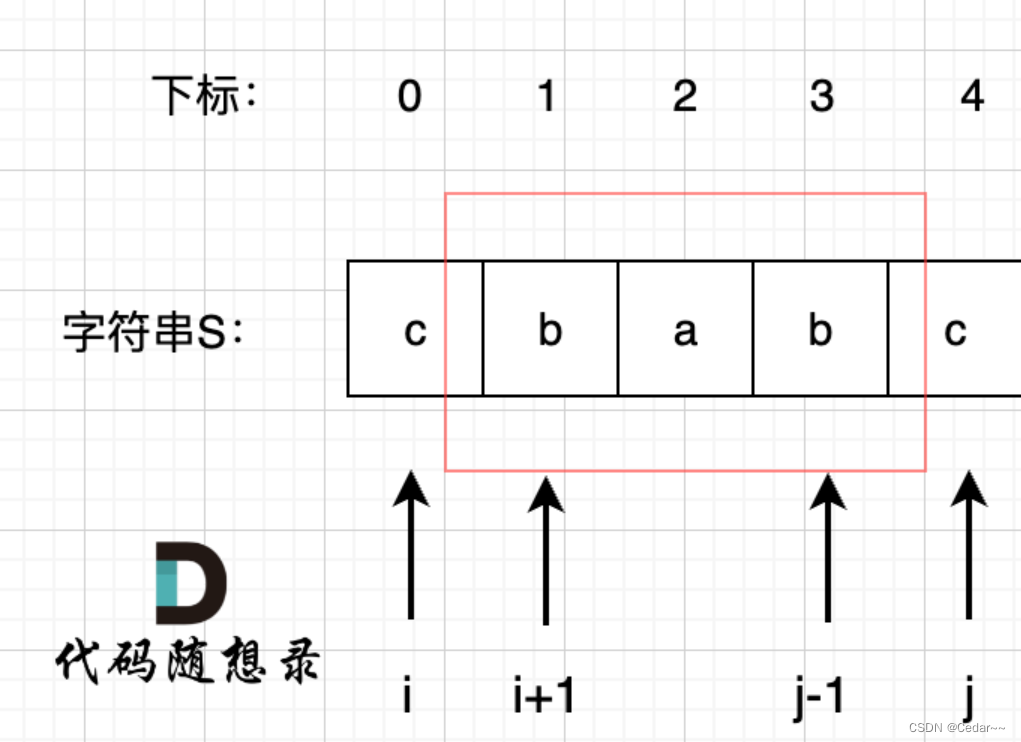
思路：动态规划
动态规划五部曲
1.定义dp数组以及下标含义
做了很多动态规划的题目。定义Dp数组很容易想到，题目要求什么，我们就定义什么
但对于【回文子串】题目来说。若定义dp[i]为以字符s.chat(i)为结尾字符串中，有多少个回文子串。
dp[i-1]和dp[i],dp[i+1] 其实没关联。需要换一种定义方式
需要看回文字符串性质来定义dp数组。如下图所示：

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

在确定s[1],s[2],s[3]为回文字符串，只需要判断s[0]是否等于s[4]。如果相同，那么s就是回文字符串
可以得到一种递推关系。即判断字符串是否回文（字符串范围【i,j]),要看【i+1,j-1]是否回文
所以定义二维Dp数组。dp[i][j].true表示闭区间【i，j]是回文字符串，false表示【i，j]不是回文字符串
2.定义递推公式
当s[i]与s[j]不相等，那没啥好说的了，dp[i][j]一定是false。
当s[i]与s[j]相等时，这就复杂一些了，有如下三种情况

情况一：下标i 与 j相同，同一个字符例如a，当然是回文子串
情况二：下标i 与 j相差为1，例如aa，也是回文子串
情况三：下标：i 与 j相差大于1的时候，例如cabac，此时s[i]与s[j]已经相同了，我们看i到j区间是不是回文子串就看aba是不是回文就可以了，那么aba的区间就是 i+1 与 j-1区间，这个区间是不是回文就看dp[i + 1][j - 1]是否为true。
3.dp数组初始化
dp数组初始化为false即可。
4.确定遍历顺序
有递推公式可得dp[i][j] 可由dp[i+1][j-1]得到
可以得出。先有 i+1,再有i.先有j-1,再有j
所以i需要从大到小遍历，j需要从小到大遍历。但因为【i,j]是闭区间，j一定是大于等于i的
所以对j遍历时，要以i为起始位置
5.举例推导dp数组
时间复杂度：O(n^2)
空间复杂度：O(n^2)

代码如下

public int countSubstrings(String s) {
    if (s == null)// 边缘条件判断
        return 0;
    if (s.equals("") || s.length() == 1)
        return 1;

    boolean[][] dp = new boolean[s.length()][s.length()];// 定义dp数组并初始化，默认值为false
    int result = 0;// 回文字符串数量
    for (int i = s.length() - 1; i >= 0; i--) {
        for (int j = i; j < s.length(); j++) {
            if (s.charAt(i) == s.charAt(j)) {
                if (i == j) {// i,j表示同一个字符
                    result++;
                    dp[i][j] = true;
                } else if (i + 1 == j) {//i,j紧挨
                    dp[i][j] = true;
                    result++;
                } else {//i,j不紧挨
                    dp[i][j] = dp[i + 1][j - 1];
                    if (dp[i][j])
                        result++;
                }
            }

        }
    }

    return result;
}

516.最长回文子序列

力扣题目链接(opens new window)

给定一个字符串 s ，找到其中最长的回文子序列，并返回该序列的长度。可以假设 s 的最大长度为 1000 。

示例 1: 输入: “bbbab” 输出: 4 一个可能的最长回文子序列为 “bbbb”。

示例 2: 输入:“cbbd” 输出: 2 一个可能的最长回文子序列为 “bb”。

提示：

1 <= s.length <= 1000
s 只包含小写英文字母

思路

思路：动态规划
1.定义dp数组以及下标含义
定义二维Dp数组。dp[i][j].表示闭区间[i,j]范围内，最长回文子序列长度
2.定义递推公式加入
当s[i]与s[j]不相等
分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。
加入s[j]的回文子序列长度为dp[i + 1][j]。
加入s[i]的回文子序列长度为dp[i][j - 1]。
那么dp[i][j]一定是取最大的，即：dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
举例如下。   s = bbbba
当i = 0 s[0] = b ,j = 4 s[4] = a
 dp[i+1][j-1] = dp[1][3] = bbb = 3;
此时分别加入s[0]和s[4]，看看哪一个可以组成最长的回文子序列。
很显然加入s[0]可以组成最长的回文子序列，长度为4

当s[i]与s[j]相等时
【i，j】闭区间内最长回文子串的长度 == dp[i+1][j-1] + 2
即dp[i][j] = dp[i+1][j-1] + 2
3.dp数组初始化
首先要考虑当i 和j 相同的情况，从递推公式：dp[i][j] = dp[i + 1][j - 1] + 2; 可以看出 递推公式是计算不到 i 和j相同时候的情况。
所以需要手动初始化一下，当i与j相同，那么dp[i][j]一定是等于1的，即：一个字符的回文子序列长度就是1。
其他情况dp[i][j]初始为0就行，这样递推公式：dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]); 中dp[i][j]才不会被初始值覆盖
4.确定遍历顺序
有递推公式可得dp[i][j] 可由dp[i+1][j-1]得到
可以得出。先有 i+1,再有i.先有j-1,再有j
所以i需要从大到小遍历，j需要从小到大遍历。但因为【i,j]是闭区间，j一定是大于等于i的
所以对j遍历时，要以i为起始位置
5.举例推导dp数组
时间复杂度：O(n^2)
空间复杂度：O(n^2)

代码如下

public static void main(String args[]) {
    longestPalindromeSubseq("bbbab");
}

public static int longestPalindromeSubseq(String s) {
    if (s.equals("")) {
        return 0;
    }
    int[][] dp = new int[s.length()][s.length()];// dp数组默认值false
    for (int i = s.length() - 1; i >= 0; i--) {
        for (int j = i; j < s.length(); j++) {
            if (s.charAt(i) == s.charAt(j)) {
                if (i == j)
                    dp[i][j] = 1;// 对dp数组的初始化。遍历过程中初始化即可
                else if (i == (j - 1))
                    dp[i][j] = 2;
                else
                    dp[i][j] = dp[i + 1][j - 1] + 2;
            } else {
                dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);
            }
        }
    }
    return dp[0][s.length() - 1];
}

问题

问题
使用52.回文子串的思路，只能求出最长连续的回文子序列
无法求出不连续的回文子序列
错误代码

public int longestPalindromeSubseq(String s) {
    if (s.equals("")) {
        return 0;
    }
    boolean[][] dp = new boolean[s.length()][s.length()];// dp数组默认值false
    int strMaxLength = 0;

    for (int i = s.length() - 1; i >= 0; i--) {
        for (int j = i; j < s.length(); j++) {
            if (s.charAt(i) == s.charAt(j)) {
                if (i == j) {
                    dp[i][j] = true;
                    if (dp[i][j]  && (j - i + 1) > strMaxLength)
                        strMaxLength = 1;
                } else if (i == j - 1) {
                    dp[i][j] = true;
                    if (dp[i][j]  && (j - i + 1) > strMaxLength)
                        strMaxLength = 2;
                } else {
                    dp[i][j] = dp[i + 1][j - 1];
                    if (dp[i][j]  && (j - i + 1) > strMaxLength)
                        strMaxLength = (j - i + 1);
                }

            }
        }
    }
    return strMaxLength;
}