数据结构与算法：图

本文介绍: 图是由顶点（vertex）和边（edge）组成的数据结构，例如fill:#333;color:#333;color:#333;fill:none;ABCD该图有四个顶点：A、B、C、D 以及四条有向边，有向图中，边是单向的。

public class FloydWarshall {
    public static void main(String[] args) {
        Vertex v1 = new Vertex("v1");
        Vertex v2 = new Vertex("v2");
        Vertex v3 = new Vertex("v3");
        Vertex v4 = new Vertex("v4");

        v1.edges = List.of(new Edge(v3, -2));
        v2.edges = List.of(new Edge(v1, 4), new Edge(v3, 3));
        v3.edges = List.of(new Edge(v4, 2));
        v4.edges = List.of(new Edge(v2, -1));
        List<Vertex> graph = List.of(v1, v2, v3, v4);

        /*
                直接连通
                v1  v2  v3  v4
            v1  0   ∞   -2  ∞
            v2  4   0   3   ∞
            v3  ∞   ∞   0   2
            v4  ∞   -1  ∞   0

                k=0 借助v1到达其它顶点
                v1  v2  v3  v4
            v1  0   ∞   -2  ∞
            v2  4   0   2   ∞
            v3  ∞   ∞   0   2
            v4  ∞   -1  ∞   0

                k=1 借助v2到达其它顶点
                v1  v2  v3  v4
            v1  0   ∞   -2  ∞
            v2  4   0   2   ∞
            v3  ∞   ∞   0   2
            v4  3   -1  1   0

                k=2 借助v3到达其它顶点
                v1  v2  v3  v4
            v1  0   ∞   -2  0
            v2  4   0   2   4
            v3  ∞   ∞   0   2
            v4  3   -1  1   0

                k=3 借助v4到达其它顶点
                v1  v2  v3  v4
            v1  0   -1   -2  0
            v2  4   0   2   4
            v3  5   1   0   2
            v4  3   -1  1   0
         */
        floydWarshall(graph);
    }

    private static void floydWarshall(List<Vertex> graph){
        int size = graph.size();
        int[][] dist = new int[size][size];
        for (int i = 0; i < size; i++) {  // 初始化
            Vertex vertex = graph.get(i);
            Map<Vertex, Integer> collect = vertex.edges.stream().collect(Collectors.toMap(v -> v.linked, v -> v.weight));
            for (int i1 = 0; i1 < size; i1++) {
                if(i == i1){
                    dist[i][i1] = 0;
                    continue;
            }
                dist[i][i1] = collect.getOrDefault(graph.get(i1),Integer.MAX_VALUE);
        }
        }
        for (int k = 0; k < size; k++) {
            for (int j = 0; j < size; j++) {
                int dist1;
                if((dist1 = dist[j][k]) < Integer.MAX_VALUE){
                    for (int i = 0; i < size; i++) {
                        int dist2;
                        if((dist2 = dist[k][i]) != Integer.MAX_VALUE)
                            dist[j][i] = Integer.min(dist1 + dist2,dist[j][i]);
                    }
                }
            }
        }

        for (int[] ints : dist) {
            for (int anInt : ints) {
                System.out.print(anInt + " ");
            }
            System.out.println();
        }
    }
}

负环

如果在 3 层循环结束后，在 dist 数组的对角线处（i==j 处）发现了负数，表示出现了负环

8) 最小生成树

图的最小生成树是一个子图，它是连通的，包含图中所有的顶点，并且所有边的权重之和最小。在最小生成树中，没有任何一条边可以被其他边替换而使得总权重变小。也就是说，最小生成树是图的所有生成树中，边的权值总和最小的生成树。

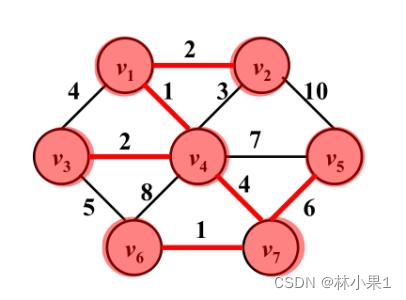
请添加图片描述

解决最小生成树问题的常用算法有Prim算法和Kruskal算法。Prim算法从一个顶点开始，每次都添加一条与当前子图连接的权重最小的边，直到所有顶点都被包含在子图中。Kruskal算法则是从所有的边开始，每次都添加一条当前所有边中权重最小的边，但需要保证添加的边不会形成环，直到所有顶点都被连接。

Prim

public class Prim {
    public static void main(String[] args) {
        Vertex v1 = new Vertex("v1");
        Vertex v2 = new Vertex("v2");
        Vertex v3 = new Vertex("v3");
        Vertex v4 = new Vertex("v4");
        Vertex v5 = new Vertex("v5");
        Vertex v6 = new Vertex("v6");
        Vertex v7 = new Vertex("v7");

        v1.edges = List.of(new Edge(v2, 2), new Edge(v3, 4), new Edge(v4, 1));
        v2.edges = List.of(new Edge(v1, 2), new Edge(v4, 3), new Edge(v5, 10));
        v3.edges = List.of(new Edge(v1, 4), new Edge(v4, 2), new Edge(v6, 5));
        v4.edges = List.of(new Edge(v1, 1), new Edge(v2, 3), new Edge(v3, 2),
                new Edge(v5, 7), new Edge(v6, 8), new Edge(v7, 4));
        v5.edges = List.of(new Edge(v2, 10), new Edge(v4, 7), new Edge(v7, 6));
        v6.edges = List.of(new Edge(v3, 5), new Edge(v4, 8), new Edge(v7, 1));
        v7.edges = List.of(new Edge(v4, 4), new Edge(v5, 6), new Edge(v6, 1));

        List<Vertex> graph = List.of(v1, v2, v3, v4, v5, v6, v7);

        prim(graph, v1);

    }

    static void prim(List<Vertex> graph, Vertex source) {
        ArrayList<Vertex> list = new ArrayList<>(graph);
        source.dist = 0;

        while (!list.isEmpty()) {
            Vertex min = chooseMinDistVertex(list);
            updateNeighboursDist(min);
            list.remove(min);
            min.visited = true;
            System.out.println("---------------");
            for (Vertex v : graph) {
                System.out.println(v);
            }
        }


    }

    private static void updateNeighboursDist(Vertex curr) {
        for (Edge edge : curr.edges) {
            Vertex n = edge.linked;
            if (!n.visited) {
                int dist = edge.weight;
                if (dist < n.dist) {
                    n.dist = dist;
                    n.prev = curr;
                }
            }
        }
    }

    private static Vertex chooseMinDistVertex(ArrayList<Vertex> list) {
        Vertex min = list.get(0);
        for (int i = 1; i < list.size(); i++) {
            if (list.get(i).dist < min.dist) {
                min = list.get(i);
            }
        }
        return min;
    }
}

Kruskal

  private static void kruskal(List<Vertex> graph,Vertex v1){
    List<Edge> edges = new ArrayList<>();
    List<Vertex> pre = new ArrayList<>();
    for (Vertex vertex : graph) {
        for (Edge edge : vertex.edges) {
            edges.add(edge);
            pre.add(vertex);
        }
    }
    for (int i = 0; i < edges.size(); i++) {
        Edge minEdge = edges.get(i);
        int min = minEdge.weight;
        for (int j = i + 1 ; j < edges.size(); j++) {
            Edge e = edges.get(j);
            if(minEdge.weight > e.weight){
                edges.set(j,minEdge);
                minEdge = e;
                edges.set(i,e);
                Vertex v = pre.get(i);
                pre.set(i,pre.get(j));
                pre.set(j,v);
            }
        }
    }
    List<Vertex> used = new ArrayList<>();
    for (int i = 0; i < edges.size(); i++) {
        Vertex v = pre.get(i);
        Vertex e = edges.get(i).linked;
        if(!used.contains(v) || !used.contains(e)){
            System.out.println(v.name + " -> " + e.name);
            used.add(v);
            used.add(e);
        }
    }
}