【Leetcode】74. 搜索二维矩阵

本文介绍: 向量的开始迭代器和结束迭代器，定义了一个范围，这个范围包含了。假设范围内的元素是已排序的。是 C++ 标准库中的一个算法，用于在排序的范围中。如果所有向量的第一个元素都不大于。如果所有向量的第一个元素都不大于。中的元素（在这里是一个向量）。是一个迭代器（iterator），它指向。小于向量的第一个元素，否则返回。中的“过去最后一个”元素的位置。所以，这行代码的效果就是找到。，这是一个特殊的迭代器，表示。中第一个其第一个元素大于。中第一个其第一个元素大于。函数返回的就是这样一个。的结果将是未定义的。

You are given an m x n integer matrix matrix with the following two properties:

Each row is sorted in non-decreasing order.
The first integer of each row is greater than the last integer of the previous row.
Given an integer target, return true if target is in matrix or false otherwise.

You must write a solution in O(log(m * n))time complexity.

Example 1:

Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
Output: true

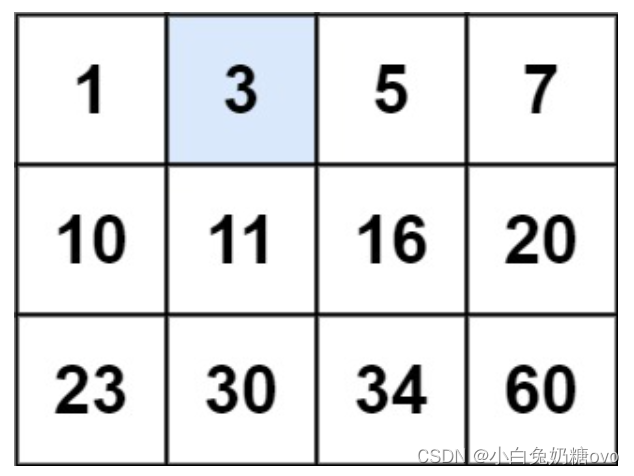
Example 2:

Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
Output: false

Constraints:

m == matrix.length
n == matrix[i].length
1 <= m, n <= 100
-104 <= matrix[i][j], target <= 104

/*
 * @lc app=leetcode.cn id=74 lang=cpp
 *
 * [74] 搜索二维矩阵
 */

// @lc code=start
class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        auto row = upper_bound(matrix.begin(), matrix.end(), target, [](const int b, const vector<int>& a) {
            return b < a[0];
        });
        if(row == matrix.begin()) {
            return false;
        }
        --row;
        return binary_search(row->begin(), row->end(), target);
    }
};
// @lc code=end

The binary_search function is a built-in function in C++ that is used to check if a particular element exists in a sorted range or not. It uses the binary search algorithm internally to perform this operation.

bool found = binary_search(startIterator, endIterator, value);

In your code, binary_search is used to check if the target exists in the row of the matrix that could potentially contain the target.

return binary_search(row->begin(), row->end(), target);

Here, row->begin() and row->end() define the range (i.e., the row in the matrix), and target is the value you’re looking for. The function will return true if the target is found in the specified row, false otherwise.

std::upper_bound() 是 C++ 标准库中的一个算法，用于在排序的范围中查找第一个大于给定值的元素的位置。

在你给出的代码中，upper_bound() 函数的使用如下：

auto row = upper_bound(matrix.begin(), matrix.end(), target, [](const int b, const vector<int>& a) {
    return b < a[0];
});

这里的 matrix.begin() 和 matrix.end() 分别返回 matrix 向量的开始迭代器和结束迭代器，定义了一个范围，这个范围包含了 matrix 向量中的所有元素。

target 是我们要查找的值。

最后一个参数是一个比较函数，它接受两个参数：一个是 target，另一个是 matrix 中的元素（在这里是一个向量）。这个函数返回 true 如果 target 小于向量的第一个元素，否则返回 false。

所以，这行代码的效果就是找到 matrix 中第一个其第一个元素大于 target 的向量的位置。如果所有向量的第一个元素都不大于 target，那么 upper_bound() 将返回 matrix.end()。

注意，upper_bound() 假设范围内的元素是已排序的。如果元素没有排序，那么 upper_bound() 的结果将是未定义的。

在这段代码中，row 是一个迭代器（iterator），它指向 matrix 中的一个元素。因为 matrix 是一个二维向量（vector<vector<int>>），所以 matrix 中的一个元素是一个 vector<int>。因此，row 的类型是 vector<vector<int>>::iterator，或者等价地，vector<int>::iterator。

upper_bound() 函数返回的就是这样一个迭代器，它指向 matrix 中第一个其第一个元素大于 target 的向量的位置。如果所有向量的第一个元素都不大于 target，那么 upper_bound() 将返回 matrix.end()，这是一个特殊的迭代器，表示 matrix 的末尾，即 matrix 中的“过去最后一个”元素的位置。