本文介绍: 腐烂的橘子
腐烂的橘子
在给定的 m x n 网格 grid 中,每个单元格可以有以下三个值之一:
- 值
0代表空单元格; - 值
1代表新鲜橘子; - 值
2代表腐烂的橘子。
每分钟,腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。
返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回 -1 。
示例 1:
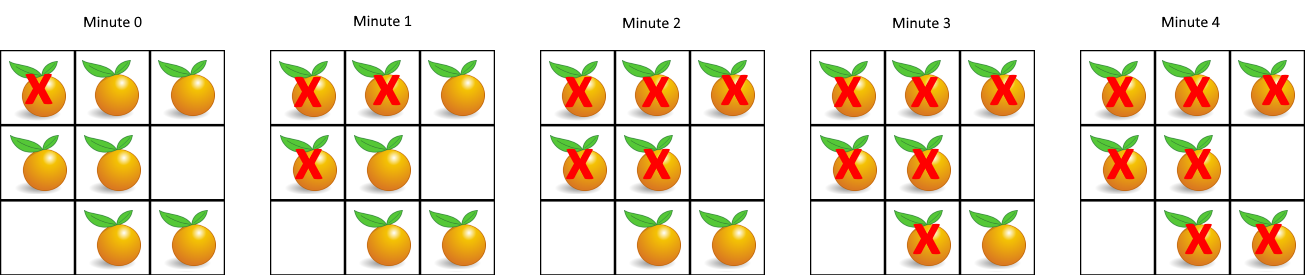
输入:grid = [[2,1,1],[1,1,0],[0,1,1]] 输出:4
方法:
广度优先遍历(BFS)
思路:
- 找出所有腐烂的橘子,将他们放入队列,作为第0层的节点
- 然后进行广度优先遍历BFS,每个节点的相邻节点可能是上下左右四个方向的节点(此处需要判断节点是否超出网格的边界)
- 由于可能存在无法被污染的橘子,需要记录新鲜橘子的数量,每遍历(污染)一个橘子,就将新鲜的橘子数量减一,如果BFS结束后,仍然存在新鲜橘子,就返回-1,否则,返回污染橘子的轮数(时间)
代码一:
class Solution {
public int orangesRotting(int[][] grid) {
// 获取数组的行数和列数
int rows = grid.length;
int cols = grid[0].length;
// 创建一个队列 用于存储橘子的信息
Queue<int[]> queue = new LinkedList<>();
// 初始化新鲜橘子的数量 0
int count = 0;
for(int row = 0; row < rows; row++){
for(int col = 0; col < cols; col++){
// 若为新鲜橘子 count++
if(grid[row][col] == 1){
count++;
}else if(grid[row][col] == 2){
// 若为腐烂橘子 将其坐标信息入队
queue.add(new int[]{row, col});
}
}
}
// 初始化腐烂的轮数(分钟数)
int sumMin = 0;
// 当还有新鲜橘子或者队列不为空时,继续腐烂橘子
while(count > 0 && ! queue.isEmpty()){
sumMin ++; // 每经过一轮循环,分钟数加一
// 获取队列的长度
int queLen = queue.size();
for(int i = 0; i < queLen; i++){
// 出队一个腐烂橘子的信息 并获取其坐标
int[] orange = queue.poll();
int r = orange[0];
int c = orange[1];
// 检查该腐烂橘子的上下左右橘子 若为新鲜橘子 对其进行腐烂处理 并入队
// 上
if(r-1 >= 0 && grid[r-1][c] == 1){
// 标记为腐烂并且入队
grid[r-1][c] = 2;
count--;
queue.add(new int[]{r-1, c});
}
// 下
if(r+1 < rows && grid[r+1][c] == 1){
// 标记为腐烂并且入队
grid[r+1][c] = 2;
count--;
queue.add(new int[]{r+1, c});
}
// 左
if(c-1 >= 0 && grid[r][c-1] == 1){
// 标记为腐烂并且入队
grid[r][c-1] = 2;
count--;
queue.add(new int[]{r, c-1});
}
// 右
if(c+1 < cols && grid[r][c+1] == 1){
// 标记为腐烂并且入队
grid[r][c+1] = 2;
count--;
queue.add(new int[]{r, c+1});
}
}
}
// 若遍历完还存在新鲜橘子 返回-1
if(count > 0){
return -1;
}else{
return sumMin; // 返回腐烂所有橘子需要的时间
}
}
}代码二:
简化之后的代码
class Solution {
public int orangesRotting(int[][] grid) {
// 获取数组的行数和列数
int rows = grid.length;
int cols = grid[0].length;
// 创建一个队列 用于存储橘子的信息
Queue<int[]> queue = new LinkedList<>();
// 初始化新鲜橘子的数量 0
int count = 0;
// 定义方向数组 分别表示向右、左、下、上移动
int[][] directions = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
for(int row = 0; row < rows; row++){
for(int col = 0; col < cols; col++){
// 若为新鲜橘子 count++
if(grid[row][col] == 1){
count++;
}else if(grid[row][col] == 2){
// 若为腐烂橘子 将其坐标信息入队
queue.add(new int[]{row, col});
}
}
}
// 初始化腐烂的轮数(分钟数)
int sumMin = 0;
// 当还有新鲜橘子或者队列不为空时,继续腐烂橘子
while(count > 0 && ! queue.isEmpty()){
sumMin ++; // 每经过一轮循环,分钟数加一
// 获取队列的长度
int queLen = queue.size();
for(int i = 0; i < queLen; i++){
// 出队一个腐烂橘子的信息 并获取其坐标
int[] orange = queue.poll();
int r = orange[0];
int c = orange[1];
// 检查该腐烂橘子的上下左右橘子 若为新鲜橘子 对其进行腐烂处理 并入队
for(int[] dir : directions){
int newRow = r + dir[0];
int newCol = c + dir[1];
if(newRow >= 0 && newRow < rows && newCol >= 0 && newCol < cols
&& grid[newRow][newCol] == 1){
count --;
grid[newRow][newCol] = 2;
queue.add(new int[]{newRow, newCol});
}
}
}
}
// 若遍历完还存在新鲜橘子 返回-1
if(count > 0){
return -1;
}else{
return sumMin; // 返回腐烂所有橘子需要的时间
}
}
}分析:
时间复杂度:O(nm)
即进行一次广度优先搜索的时间,其中 n=grid.lengthn=grid.lengthn=grid.length, m=grid[0].lengthm=grid[0].lengthm=grid[0].length 。
空间复杂度:O(nm)
需要额外的 disdisdis 数组记录每个新鲜橘子被腐烂的最短时间,大小为 O(nm)O(nm)O(nm),且广度优先搜索中队列里存放的状态最多不会超过 nmnmnm 个,最多需要 O(nm)O(nm)O(nm) 的空间,所以最后的空间复杂度为 O(nm)O(nm)O(nm)。
原文地址:https://blog.csdn.net/m0_67281369/article/details/135779617
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_61945.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!
主题授权提示:请在后台主题设置-主题授权-激活主题的正版授权,授权购买:RiTheme官网
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。