一、引言
逻辑回归中的损失函数通常采用的是交叉熵损失函数（cross-entropy loss function）。在逻辑回归中，我们通常使用sigmoid函数将线性模型的输出转换为概率值，然后将这些概率值与实际标签进行比较，从而计算损失。
二、交叉熵损失函数
在逻辑回归解决二分类问题的学习中，我们认识到逻辑回归的输出结果可以看成输入时输出为正例（
)的概率。
分解如下：
于是我们便想到可以通过比较模型预测的概率分布和实际标签之间的差异来衡量模型的准确性。在信息论中，交叉熵用来比较两个概率分布之间的差异。
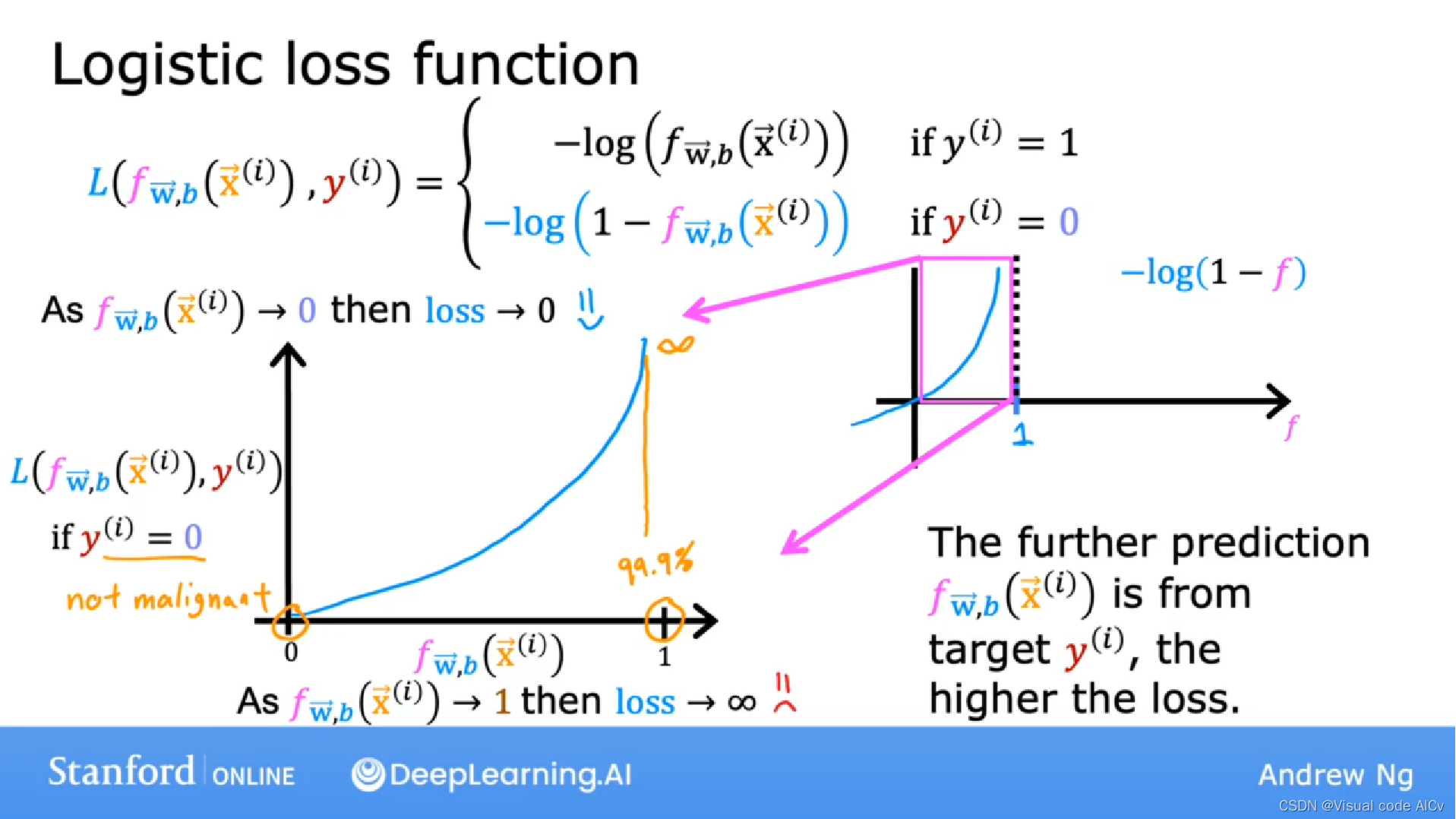
定义：交叉熵损失函数（Cross-entropy loss function）是一种用于衡量模型输出与实际标签之间差异的损失函数。在机器学习中，交叉熵损失函数通常用于分类问题中，特别是在逻辑回归和神经网络等模型中。
对于一个逻辑回归函数：
损失函数公式：
简化后的公式：
（整体）损失函数：
根据损失函数的定义，当的值与目标值
越接近，损失函数值越小，预测越准确。
所以：
以预测肿瘤的例子说明，如果模型预测患者的肿瘤极大概率（如99.9%）是恶性，而实际却不是恶性，我们会得到一个极大的损失函数值。简单来说，模型的预测值距离y的真实值越远，损失越大。
三、为什么不使用均方差损失函数
非凸性：均方差损失函数在逻辑回归中会导致损失函数变成非凸函数，这会导致优化过程变得非常困难。因为非凸函数有多个局部最小值， 而均方差损失函数可能会陷入局部最小值而无法到达全局最小值，这回影响模型的训练效果。
输出范围不同：逻辑回归的输出是概率值，范围在0到1之间，而均方差损失函数对于这种概率输出不敏感，它对于离群值（outliers）非常敏感。这意味着即使是一个很小的偏离，也会导致损失函数变得非常大，从而使得模型对于异常值非常敏感。
四、梯度下降实现
在线性回归中，我们引入了一种用于求解模型的方法——梯度下降法。对于逻辑回归模型，我们也可以采用相同的方法。
对于(整体)损失函数：
进行以下操作：
repeat{
}simultaneous updates
我们不难发现，逻辑回归的梯度下降和之前线性回归中的梯度下降基本一致，唯一不同的是发生了变化。 所以在逻辑回归中也可以使用特征缩放的方法加快梯度下降法的收敛速度。
原文地址:https://blog.csdn.net/m0_65995252/article/details/135675959
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
如若转载，请注明出处：http://www.7code.cn/show_62035.html
如若内容造成侵权/违法违规/事实不符，请联系代码007邮箱：suwngjj01@126.com进行投诉反馈，一经查实，立即删除！
