坚持刷题 ｜ 平衡二叉树

坚持刷题，老年痴呆追不上我，今天继续二叉树：平衡二叉树

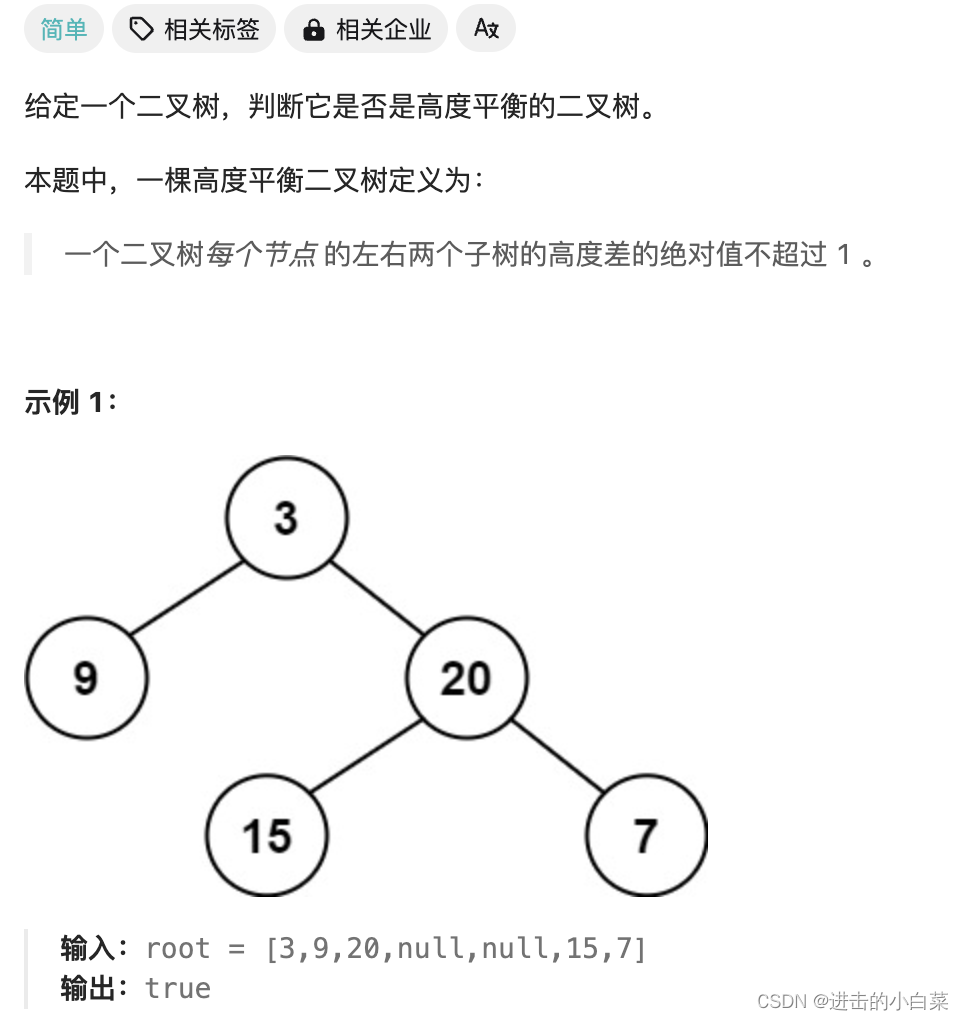
题目

110.平衡二叉树

考察点

• 递归能力： 能否使用递归来解决问题。
• 树的基本操作：能否正确地访问节点的值，左子树，右子树等。
• 理解平衡二叉树：能够理解平衡二叉树的定义。
• 边界条件处理： 能否正确处理空树的情况。
• 时间和空间复杂度： 解决问题的方法是否具有合理的时间和空间复杂度。

代码实现

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode(int x) {
        val = x;
    }
}

public class BinaryTreeBalance {

    public boolean isBalanced(TreeNode root) {
        if (root == null) {
            return true;
        }

        int leftHeight = getHeight(root.left);
        int rightHeight = getHeight(root.right);

        // 检查当前节点是否平衡，并递归检查左右子树
        return Math.abs(leftHeight - rightHeight) <= 1
                && isBalanced(root.left)
                && isBalanced(root.right);
    }

    private int getHeight(TreeNode node) {
        if (node == null) {
            return 0;
        }

        // 递归计算左右子树的高度，取最大值加上当前节点的高度（1）
        return 1 + Math.max(getHeight(node.left), getHeight(node.right));
    }

    public static void main(String[] args) {
        BinaryTreeBalance solution = new BinaryTreeBalance();

        // 在这里构建你的二叉树
        TreeNode root = new TreeNode(1);
        root.left = new TreeNode(2);
        root.right = new TreeNode(3);
        root.left.left = new TreeNode(4);
        root.left.right = new TreeNode(5);

        // 调用isBalanced方法判断是否为平衡二叉树
        boolean result = solution.isBalanced(root);

        // 输出结果
        System.out.println("Is the binary tree balanced? " + result);
    }
}

实现总结

• 递归：使用递归来计算每个节点的高度，参考 坚持刷题｜二叉树的最大深度，检查左右子树的高度差是否超过1，若超过1，则说明不是平衡二叉树
• 时间复杂度： O(n log n)。因为对于每个节点，都需要计算其左右子树的高度，而计算高度的时间复杂度是 O(log n)
• 空间复杂度： O(log n)，递归调用栈的深度等于该节点的高度。在平衡二叉树的情况下，树的高度是 O(log n) 级别的。因此，递归调用的空间复杂度是 O(log n)。需要注意的是，这里的空间复杂度并不仅仅是由递归调用所使用的空间构成，还包括了递归过程中的临时变量、参数传递等所占用的空间。

对实现进一步改进

避免重复计算节点的高度： 在上面的实现中，对每个节点都调用了getHeight方法来计算高度。这可能导致重复计算，尤其是对于同一个节点。为了避免这种情况，可以修改算法，使得在计算高度的同时判断平衡条件。
一边计算高度一边判断平衡条件： 可以在递归调用的过程中，一边计算左右子树的高度，一边判断当前节点是否满足平衡条件。这样可以避免递归两次计算相同节点的高度。

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode(int x) {
        val = x;
    }
}

public class BalancedBinaryTree {

    public boolean isBalanced(TreeNode root) {
        return checkHeightAndBalance(root) != -1;
    }

    private int checkHeightAndBalance(TreeNode node) {
        if (node == null) {
            return 0;  // 空树是平衡的，高度为0
        }

        int leftHeight = checkHeightAndBalance(node.left);
        if (leftHeight == -1) {
            return -1;  // 左子树不平衡，直接返回-1
        }

        int rightHeight = checkHeightAndBalance(node.right);
        if (rightHeight == -1) {
            return -1;  // 右子树不平衡，直接返回-1
        }

        // 判断当前节点是否平衡，如果不平衡则返回-1，否则返回当前节点的高度
        if (Math.abs(leftHeight - rightHeight) > 1) {
            return -1;
        } else {
            return Math.max(leftHeight, rightHeight) + 1;  // 返回当前节点的高度
        }
    }

    public static void main(String[] args) {
        BalancedBinaryTree solution = new BalancedBinaryTree();

        // 在这里构建你的二叉树
        TreeNode root = new TreeNode(1);
        root.left = new TreeNode(2);
        root.right = new TreeNode(3);
        root.left.left = new TreeNode(4);
        root.left.right = new TreeNode(5);

        // 调用isBalanced方法判断是否为平衡二叉树
        boolean result = solution.isBalanced(root);

        // 输出结果
        System.out.println("Is the binary tree balanced? " + result);
    }
}

在这个改进的实现中，checkHeightAndBalance方法返回-1表示不平衡，否则返回当前节点的高度。这样可以在计算高度的同时判断平衡条件，避免了重复计算。

扩展提问

可以用非递归的方式实现吗？时间复杂度和空间复杂度又会如何呢？

代码007普通

打赏 收藏 海报 链接