C/C++ LeetCode:跳跃问题_代码007(未授权)

本文介绍: 区间覆盖，我们可以每次移动一位的时候就进行一次区间覆盖的估计，然后将区间覆盖最大的来更新旧的，如果区间将数组的最后一个元素覆盖了之后，就证明我们肯定能保证能存在一个最短的路径，使得步数最小。数组的第一个元素是2，那我们是不是要往后移动2个元素，才能保证步数最短呢？显然不是，如果我们直接往后移了2位，是比只移了1位的距离远（从下标为 0 跳到下标为 1 的位置，跳 1步，然后跳 3 步到达数组的最后一个位置。可是每一步都尽可能的大，这句话可能会有一些歧义。题目让我们来解答如何才能在最短的步数内到达终点。

题目链接：45. 跳跃游戏 II – 力扣（LeetCode）

给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。

每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说，如果你在 nums[i] 处，你可以跳转到任意 nums[i + j] 处:

0 <= j <= nums[i]

i + j < n

返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。

示例 1:
输入: nums = [2,3,1,1,4]
输出: 2
解释:    跳到最后一个位置的最小跳跃数是 2。
        从下标为 0 跳到下标为 1 的位置，跳 1步，然后跳 3 步到达数组的最后一个位置。
示例 2:
输入: nums = [2,3,0,1,4]
输出: 2
提示:

1 <= nums.length <= 104

0 <= nums[i] <= 1000

题目保证可以到达 nums[n-1]

`二、理解`

题目让我们来解答如何才能在最短的步数内到达终点。我们都知道要每一步都尽可能的大，才能以最少的步数到达终点。可是每一步都尽可能的大，这句话可能会有一些歧义。

就比如说这个数组，如何才叫尽可能的大呢？

数组的第一个元素是2，那我们是不是要往后移动2个元素，才能保证步数最短呢？显然不是，如果我们直接往后移了2位，是比只移了1位的距离远（在这步上体现）。但是如果你移动了1位之后，接下来就可以移3位；而移动了2位之后，接下来只能移动1位。那如何解决呢？

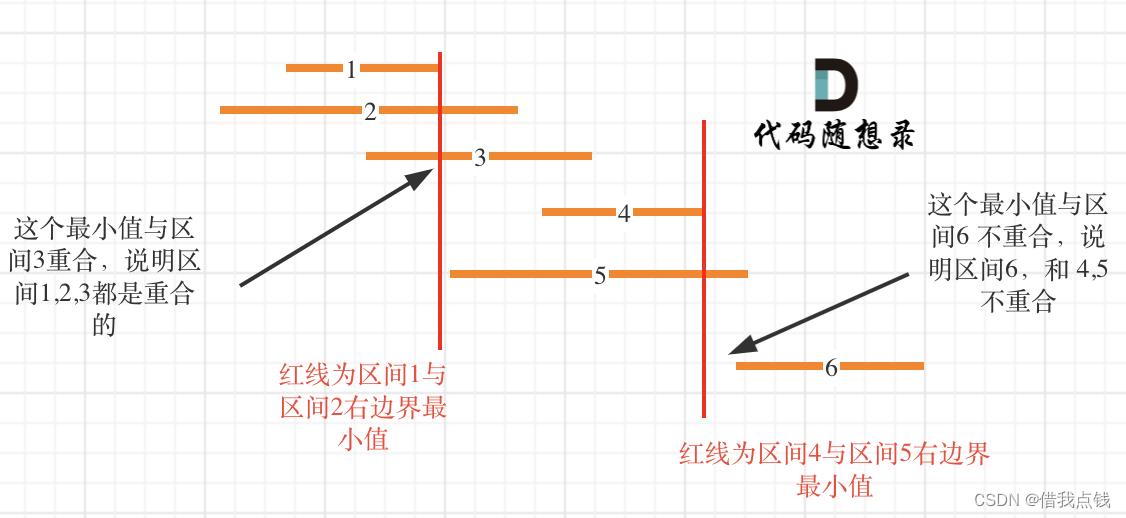
区间覆盖，我们可以每次移动一位的时候就进行一次区间覆盖的估计，然后将区间覆盖最大的来更新旧的，如果区间将数组的最后一个元素覆盖了之后，就证明我们肯定能保证能存在一个最短的路径，使得步数最小。

class Solution {
public:
    int jump(vector<int>& nums) {
        // 区间覆盖
        if (nums.size() == 1) return 0; 
        int cur = 0;// 当前覆盖区间
        int next = 0;// 下个状态的覆盖区间
        int step = 0;// 步数
        // 循环遍历每个数
        for (int i = 0; i < nums.size(); i ++ )
        {
            next = max(next, i + nums[i]);// 更新最大的区间
            if (cur == i)// 如果i 和覆盖区间的右端点相等的时候，代表该覆盖区间遍历完毕，需要更新新的区间
            {
                cur = next;
                step ++;// 每次区间更新相当于一次步数的跳跃
                if (cur == nums.size() - 1)// 如果区间包含最后一个元素的时候，就得到最短的步数，跳出循环
                {
                    break;
                }
            }
        }
        return step;
    }
};

显示所有内容

声明：本站所有文章，如无特殊说明或标注，均为本站原创发布。任何个人或组织，在未征得本站同意时，禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益，可联系我们进行处理。