【算法小记】——机器学习中的概率论和线性代数，附线性回归matlab例程

=[1x1​​1x2​​……​1xn​​]T

使用matlab计算解析解

%% 使用最小二乘法计算数据的线性回归最优解

clear all;
clc;

x = [75, 71, 83, 74, 73, 67, 79, 73, 88, 80, 81, 78, 73, 68, 71]';
y = [183, 175, 187, 185, 176, 176, 185, 191, 195 ,185, 174, 180, 178, 170, 184]';

X =[ones(15, 1), x]; %生成x的转置扩充数据

X_T = transpose(X);  %转置
a_start = inv(X_T * X)*X_T*y; % inv计算矩阵的拟，得到线性估计的参数a和b，这里是解析解

x_draw = 65:0.1:90;
scatter(X(:, 2), y, 80, "r");   % 原始数据的散点图
hold on;
plot(x_draw, a_start(2)*x_draw+a_start(1)); % 解析解的线性回归结果
grid on;

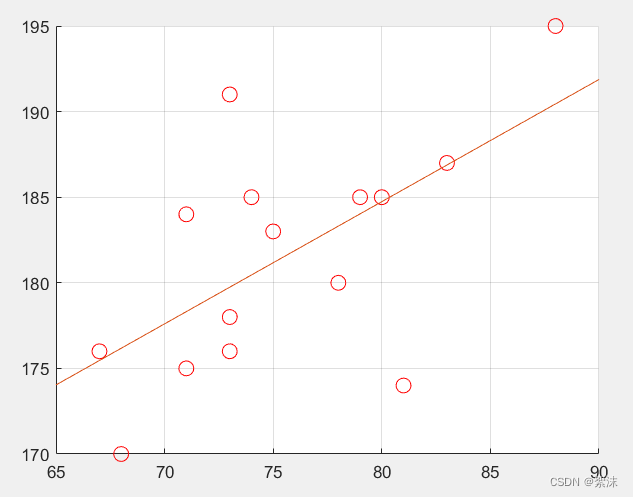
上图是最小二乘法的最优计算结果。

使用matlab通过梯度下降迭代计算解

%% 使用ML的梯度下降法迭代计算参数
clear all;
clc;

x = [75, 71, 83, 74, 73, 67, 79, 73, 88, 80, 81, 78, 73, 68, 71]';
y = [183, 175, 187, 185, 176, 176, 185, 191, 195 ,185, 174, 180, 178, 170, 184]';

%% 解析解
X =[ones(15, 1), x]; %生成x的转置扩充数据

X_T = transpose(X);  %转置
a_start = inv(X_T * X)*X_T*y; % inv计算矩阵的拟，得到线性估计的参数a和b，这里是解析解

x_draw = 65:0.1:90;
scatter(X(:, 2), y, 80, "r");   % 原始数据的散点图
hold on;
plot(x_draw, a_start(2)*x_draw+a_start(1)); % 解析解的线性回归结果
grid on;

%% 梯度下降回归解
%     1、定义参数，初始化矩阵
 %    2、while 循环 y = y - lr * x'
 ab_start = [100 ; 2];   % 设置一个初始值
 
 % 学习率
 learning_reate = 0.00002; 
 %learning_reate = [0.001 0; 0 0.00001]; % 使用二阶学习率适应原始数据的倍率
    
 % 迭代
 for i = 1:100000
       ab_start = ab_start - learning_reate * X_T *( -y +X* ab_start);  % 计算代价函数对参数矩阵的梯度，用原参数减学习率乘梯度
 end

此时可以看出ab_start 作为迭代计算得到的结果已经拟合于解析解算的结果了。

代码007普通

打赏 收藏 海报 链接