本文介绍: 今天同样是01背包问题,今天详细学习了背包问题在各种场景下的应用。今天一道也没做出来,有点废。好难啊!就是思路不太清晰,不知道如何去做,看了题解后感觉原来如此,但是想不出来。今天做的时候有几道题思路基本差不多,但是想着想着就懵了,直接把自己绕进去了。本题与昨天的最后一题有点相像,基本思路一致。只不过昨天那题是求两子集相等的时候,本题可以看作求两子集的相差最小同样动态规划五部曲:1.确定dp数组的含义dp[j] 表示容量(这里说容量更形象,其实就是重量)为j的背包,最多可以背最大重量为dp[j]。
前言:
今天同样是01背包问题,今天详细学习了背包问题在各种场景下的应用。今天一道也没做出来,有点废。好难啊!就是思路不太清晰,不知道如何去做,看了题解后感觉原来如此,但是想不出来。今天做的时候有几道题思路基本差不多,但是想着想着就懵了,直接把自己绕进去了。
第一题:

简介:
本题与昨天的最后一题有点相像,基本思路一致。只不过昨天那题是求两子集相等的时候,本题可以看作求两子集的相差最小
同样动态规划五部曲:
1.确定dp数组的含义
dp[j] 表示容量(这里说容量更形象,其实就是重量)为j的背包,最多可以背最大重量为dp[j]。
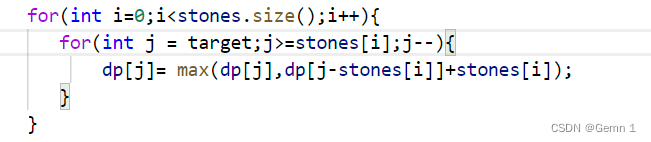
代码实现:
第二题:
简介:
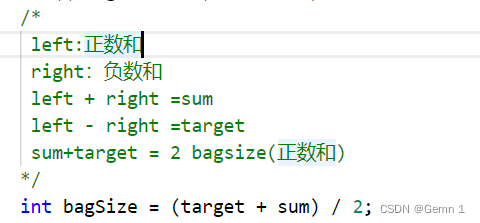
代码实现:
第三题:
简介:
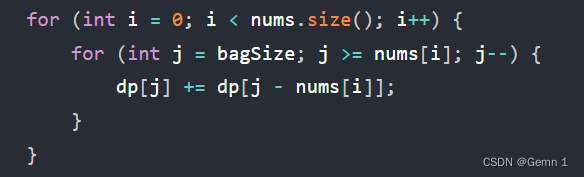
代码实现:
总结:
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。




![C++ [NOIP2007 提高组] 矩阵取数游戏](http://www.7code.cn/wp-content/uploads/2023/11/ee6748cbc735e6105405f8a984d954c804b93f34bc916-Z0IqTf_fw1200.png)