【蓝桥杯冲冲冲】动态规划学习 [NOIP2003 提高组] 加分二叉树

【蓝桥杯冲冲冲】动态规划学习 [NOIP2003 提高组] 加分二叉树

蓝桥杯备赛 | 洛谷做题打卡day24

• [NOIP2003 提高组] 加分二叉树

  题目描述

  设一个

  n

  n

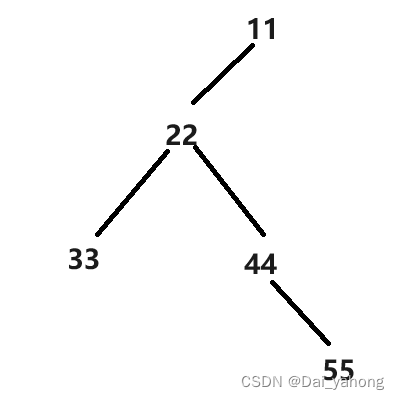
  n 个节点的二叉树

  tree

  text{tree}

  tree 的中序遍历为

  (

  1

  ,

  2

  ,

  3

  ,

  …

  ,

  n

  )

  (1,2,3,ldots,n)

  (1,2,3,…,n)，其中数字

  1

  ,

  2

  ,

  3

  ,

  …

  ,

  n

  1,2,3,ldots,n

  1,2,3,…,n 为节点编号。每个节点都有一个分数（均为正整数），记第

  i

  i

  i 个节点的分数为

  d

  i

  d_i

  di​，

  tree

  text{tree}

  tree 及它的每个子树都有一个加分，任一棵子树

  subtree

  text{subtree}

  subtree（也包含

  tree

  text{tree}

  tree 本身）的加分计算方法如下：

  subtree

  text{subtree}

  subtree 的左子树的加分

  ×

  times

  ×

  subtree

  text{subtree}

  subtree 的右子树的加分

  +

  +

  +

  subtree

  text{subtree}

  subtree 的根的分数。

  若某个子树为空，规定其加分为

  1

  1

  1，叶子的加分就是叶节点本身的分数。不考虑它的空子树。

  试求一棵符合中序遍历为

  (

  1

  ,

  2

  ,

  3

  ,

  …

  ,

  n

  )

  (1,2,3,ldots,n)

  (1,2,3,…,n) 且加分最高的二叉树

  tree

  text{tree}

  tree。要求输出

  1. tree

     text{tree}

     tree 的最高加分。

  2. tree

     text{tree}

     tree 的前序遍历。

  输入格式

  第

  1

  1

  1 行

  1

  1

  1 个整数

  n

  n

  n，为节点个数。

  第

  2

  2

  2 行

  n

  n

  n 个用空格隔开的整数，为每个节点的分数

  输出格式

  第

  1

  1

  1 行

  1

  1

  1 个整数，为最高加分（$ Ans le 4,000,000,000$）。

  第

  2

  2

  2 行

  n

  n

  n 个用空格隔开的整数，为该树的前序遍历。

  样例 #1

  样例输入 #1

  5
  5 7 1 2 10
  

  样例输出 #1

  145
  3 1 2 4 5
  

  提示

  数据规模与约定

  对于全部的测试点，保证

  1

  ≤

  n

  <

  30

  1 leq n< 30

  1≤n<30，节点的分数是小于

  100

  100

  100 的正整数，答案不超过

  4

  ×

  1

  0

  9

  4 times 10^9

  4×109。

  

思路

一道入门的区间dp，当然，根据写法不同你还可以把它归类为树形dp或者记忆化搜索，其实都无所谓啦。
作为一道入门题，我们完全可以“显然”地做出来，但是在这里还是想和大家回顾下动态规划以及区间动规。

Q：dp特点是什么？
A：dp把原问题视作若干个重叠的子问题的逐层递进，每个子问题的求解过程都会构成一个“阶段”，在完成一个阶段后，才会执行下一个阶段。
Q：dp要满足无后效性，什么叫无后效性？
A：已经求解的子问题不受后续阶段的影响。

有人觉得dp很抽象，那是因为没有一步一步来想，直接听别人的结论，我们在这里以这道题为例，一步一步来推导。

首先，我们要做的就是设计状态，其实就是设计dp数组的含义，它要满足无后效性。
关注这个 左子树*右子树+根 我只要知道左子树分数和右子树分数和根的分数（已给出），不就可以了吗？管他子树长什么样！
所以，我们f数组存的就是最大分数，怎么存呢？
我们发现：子树是一个或多个节点的集合。

题解代码

学会利用新知，自己多试试并尝试积攒一些固定解答方案，debug，以下是题解代码 ~

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int MAXN = 50;
typedef long long ll;
ll n;
ll f[MAXN][MAXN], root[MAXN][MAXN];

void print(ll l, ll r) {
	if (l > r)return;
	printf("%lld ", root[l][r]);
	if (l == r)return;
	print(l, root[l][r] - 1);
	print(root[l][r]+1,r);
}

int main() {
	scanf("%lld", &n);
	for (int i = 1; i <= n; i++)scanf("%lld", &f[i][i]),f[i][i-1]=1, root[i][i] = i;
	for (int len = 1; len < n; ++len) {
		for (int i = 1; i + len <= n; ++i) {
			int j = i + len;
			f[i][j] = f[i + 1][j] + f[i][i];//默认它的左子树为空，如果有的话，这肯定不是最优解
			root[i][j] = i;//默认从起点选根
			for (int k = i + 1; k < j; ++k) {
				if (f[i][j] < f[i][k - 1] * f[k + 1][j] + f[k][k]) {
					f[i][j] = f[i][k - 1] * f[k + 1][j] + f[k][k];
					root[i][j] = k;
				}
			}
		}
	}
	cout << f[1][n] << endl;
	print(1, n);
	return 0;
}

我的一些话

• 今天学习动态规划，dp属于比较难的部分，需要多动脑，多思考思路还是很好掌握的，虽然一次性AC有一定难度，需要通盘的考虑和理解，以及扎实的数据结构基础才能独立写出AC代码。但无论难易，大家都要持续做题，保持题感喔！一起坚持(o´ω`o)

• 如果有非计算机专业的uu自学的话，关于数据结构的网课推荐看b站上青岛大学王卓老师的课，讲的很细致，有不懂都可以私信我喔

• 总结来说思路很重要，多想想，多在草稿纸上画画，用测试数据多调试，debug后成功编译并运行出正确结果真的会感到很幸福！

• 关于之前蓝桥杯备赛的路线和基本方法、要掌握的知识，之前的博文我都有写，欢迎大家关注我，翻阅自取哦~

• 不管什么都要坚持吧，三天打鱼两天晒网无法形成肌肉记忆和做题思维，该思考的时候一定不要懈怠，今天就说这么多啦，欢迎评论留言，一起成长：）

代码007普通

打赏 收藏 海报 链接