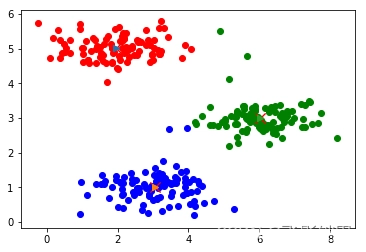
本文介绍: K-均值聚类(K-means clustering)是一种常用的无监督学习算法,用于将数据集划分成 K 个不重叠的簇(cluster)。该算法通过迭代的方式将样本点划分到 K 个簇中,使得同一簇内的样本点相似度较高,而不同簇之间的样本点相似度较低。为了克服这些缺点,有很多改进的K-均值聚类算法被提出,如谱聚类、层次聚类等。
K-均值聚类(K-means clustering)是一种常用的无监督学习算法,用于将数据集划分成 K 个不重叠的簇(cluster)。该算法通过迭代的方式将样本点划分到 K 个簇中,使得同一簇内的样本点相似度较高,而不同簇之间的样本点相似度较低。
算法步骤:
优点:
缺点:
为了克服这些缺点,有很多改进的K-均值聚类算法被提出,如谱聚类、层次聚类等。
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。