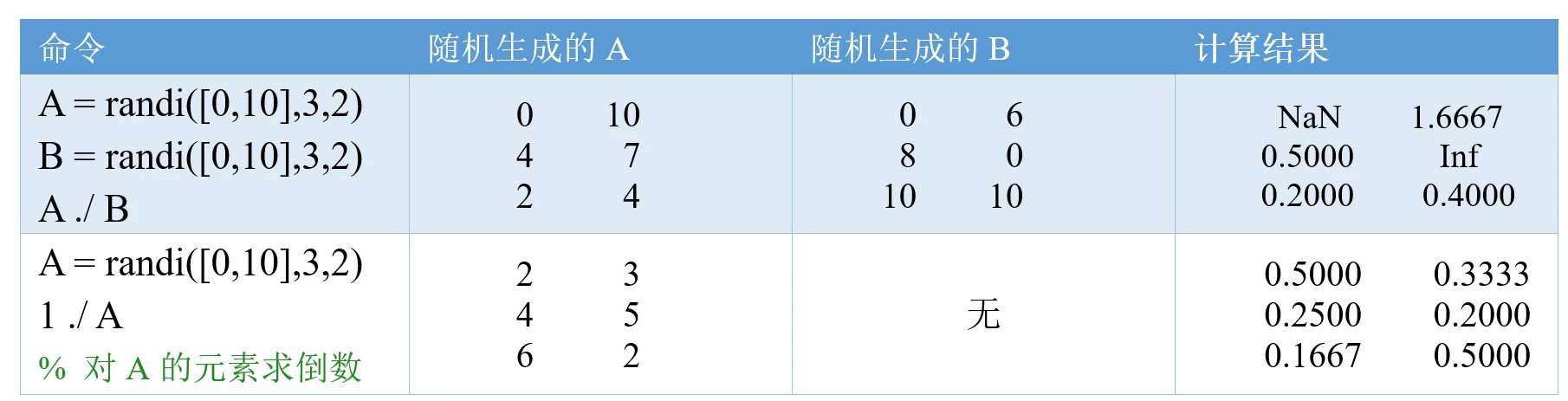
本文介绍: 六—二次型二—矩阵逆矩阵抽象矩阵求逆数字型矩阵求逆二阶矩阵求逆秒杀解矩阵方程方阵伴随矩阵三—向量组的线性相关性线性表示数字型向量组 线性相关性判断抽象型向量组 线性相关性判断向量组的秩与极大无关组四—线性方程组齐次方程组基础解系通解非齐次方程组通解带参数方程组的求解五—矩阵的特征值与特征向量数字形特征值与特征向量求法抽象形特征值与特征向量求法矩阵的相似对角化对称矩阵的相似对角化 与正交矩阵。
二—矩阵
逆矩阵

抽象矩阵求逆

数字型矩阵求逆

二阶矩阵求逆秒杀

解矩阵方程


方阵


伴随矩阵



三—向量组的线性相关性
线性表示

数字型向量组 线性相关性判断


抽象型向量组 线性相关性判断


向量组的秩与极大无关组

四—线性方程组
齐次方程组

基础解系

通解

非齐次方程组

通解
带参数方程组的求解

五—矩阵的特征值与特征向量
数字形
特征值与特征向量求法





抽象形
特征值与特征向量求法


矩阵的相似对角化



对称矩阵的相似对角化 与正交矩阵


正交矩阵

施密特正交化简化为叉乘
同一个特征值求出的两个特征向量 需要正交化
与秩的第一行求法向量 即为第二个正交向量
再分别单位化即可
整理一些名词
极大无关组:阶梯型拐弯处
基础解系=特征向量:阶梯型非拐弯处
六—二次型
二次型的矩阵表示

化二次型为标准型
配方法


正交变化法


正定二次型/正定矩阵


原文地址:https://blog.csdn.net/m0_71819030/article/details/135773000
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_65457.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。