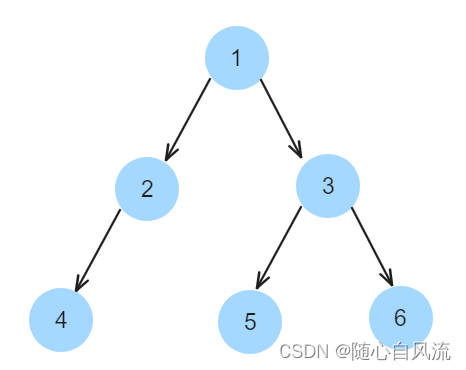
669. 修剪二叉搜索树
这道题目比较难,比 添加增加和删除节点难的多,建议先看视频理解。
题目链接/文章讲解: 代码随想录
视频讲解: 你修剪的方式不对,我来给你纠正一下!| LeetCode:669. 修剪二叉搜索树_哔哩哔哩_bilibili
递归的做法是将首先确定当前节点的值是否小于左边界,如果小于左边界,那么就给它的祖先节点返回当前节点的右孩子(注意不是直接返回右孩子,而是它的返回递归函数),同理如果它的值大于右边界,就返回当前节点的左孩子,如果恰好在边界内部,那就将它的左右孩子处理一下,处理成在边界内部的,然后返回当前节点——
TreeNode* trimBST(TreeNode* root, int low, int high) {
if(root==NULL) return root;
TreeNode* tmp=root;
if(root->val<low){
return trimBST(root->right,low,high);
}
if(root->val>high){
return trimBST(root->left,low,high);
}
root->left=trimBST(root->left,low,high);
root->right=trimBST(root->right,low,high);
return root;
}文章给出的迭代做法主要分成三部分:
- 处理根节点,使得根节点符合要求,如果不符合就一直移动根节点,直至指向符合要求的节点
- 处理剩下的节点,使得满足大于左边界
- 处理剩下的节点,使得满足小于右边界
这道题首先处理根节点,是因为一旦根节点符合要求了,那么在处理剩下的两个步骤的时候就会简单很多,因为小于左边界的节点只能是在根节点的左边,而大于右边界的节点只能在根节点的右边。
在处理剩下两个步骤的时候,比如第二步,要使得指针一直向着左孩子移动,因为这样才能找到最小的;
由于要改变节点的指向,所以指针不能直接指向要处理的节点(也就是当前节点),而是要指向它的父母节点;
如果遇到某个节点的左孩子的值小于左边界,那就要一直执行将左孩子的右孩子赋值给当前节点的左孩子,直到使得当前节点满足要求为止,这样就能保证,当前节点以及它的右孩子一定是大于左边界的,这样再移动到当前节点的左孩子——
TreeNode* trimBST(TreeNode* root, int L, int R) {
if (!root) return nullptr;
// 处理头结点,让root移动到[L, R] 范围内,注意是左闭右闭
while (root != nullptr && (root->val < L || root->val > R)) {
if (root->val < L) root = root->right; // 小于L往右走
else root = root->left; // 大于R往左走
}
TreeNode *cur = root;
// 此时root已经在[L, R] 范围内,处理左孩子元素小于L的情况
while (cur != nullptr) {
while (cur->left && cur->left->val < L) {
cur->left = cur->left->right;
}
cur = cur->left;
}
cur = root;
// 此时root已经在[L, R] 范围内,处理右孩子大于R的情况
while (cur != nullptr) {
while (cur->right && cur->right->val > R) {
cur->right = cur->right->left;
}
cur = cur->right;
}
return root;
}这是我自己写的迭代,和文章里面有异曲同工之处,我并没有首先处理根节点,而是直接将过程分成保证左边界符合要求和保证右边界符合要求,故而在这过程中,必然有可能存在根节点的变化,所以要及时更新根节点。
对于如何保证边界,比如保证左边界,首先判断当前节点是否越界,如果已经越界,那就需要进一步判断当前节点的父母节点是否为空,如果pre为空,就证明当前节点一定是根节点,根节点不符合要求,那就要直接更新根节点(更新为之前根节点的右孩子),而且不需要对pre进行更新,是因为修改的是根节点,而根节点的父母节点固定是NULL;
如果pre不为空,就证明不是根节点,那就要让当前节点的父母节点的左孩子指向更新为当前节点的右孩子(一定是更新的父母节点的左孩子,是因为全程都是将节点在向左移动,不会涉及到右孩子);
无论pre是否为空,也就是无论是否根节点出现问题,都要将当前节点移动到它的右孩子(不用管它的左孩子,因为左孩子一定更小,更不符合要求),因为当前节点和它的左孩子都已经被舍弃;
而如果当前节点符合要求,那么就要更新pre节点,将节点移动到当前节点的左孩子——
TreeNode* trimBST(TreeNode* root, int low, int high) {
if(root==NULL) return root;
TreeNode* pre=NULL;
TreeNode* newRoot=root;
while(root){
if(root->val<low){
if(!pre) {
newRoot=root->right;
}else pre->left=root->right;
root=root->right;
}else{
pre=root;
root=root->left;
}
}
root=newRoot;
pre=NULL;
while(root){
if(root->val>high){
if(!pre) {
newRoot=root->left;
}else {
pre->right=root->left;
}
root=root->left;
}else {
pre=root;
root=root->right;
}
}
return newRoot;
}108.将有序数组转换为二叉搜索树
本题就简单一些,可以尝试先自己做做。
这道题平衡是最不需要注意的点,几乎能创建就会创建一个平衡的二叉搜索树,所以重点再利用有序数组创建搜索二叉树。
这道题使用递归很好解决,主要是注意:去两个下标的中点的话是(left+right)/2,而不是(right-left)/2——
TreeNode* buildBST(vector<int>& nums,int left,int right){
if(right-left==0) return NULL;
TreeNode* node=new TreeNode(nums[(right+left)/2]);
if(right-left==1) return node;
node->left=buildBST(nums,left,(right+left)/2);
node->right=buildBST(nums,(right+left)/2+1,right);
return node;
}
TreeNode* sortedArrayToBST(vector<int>& nums) {
return buildBST(nums,0,nums.size());
}迭代法。注意文章里面这次使用的不是左闭右开区间而是左闭右闭区间。这道题无关出队的先后顺序,只要每次三个容器的对应位置的内容是相互匹配的就行,所以也可以用三个栈来实现,大差不差。用容器来储存左右区间下标,因为左右区间下标不能实现同时更新,而且更新的顺序不固定,所以需要使用两个容器来储存。
每次取出要遍历的一个节点,给它赋值(通过它的左右区间下标来确定它的值,它的值一定是区间中点处的值),然后考虑当前节点是否存在左右孩子(通过左右区间下标和中点下标来判断),如果存在左右孩子,那就先将一个无效节点储存进去(这时候的值是没有意义的,需要在弹出的时候重新赋值),然后更新相应的区间下标——
TreeNode* sortedArrayToBST(vector<int>& nums) {
if (nums.size() == 0) return nullptr;
TreeNode* root = new TreeNode(0); // 初始根节点
queue<TreeNode*> nodeQue; // 放遍历的节点
queue<int> leftQue; // 保存左区间下标
queue<int> rightQue; // 保存右区间下标
nodeQue.push(root); // 根节点入队列
leftQue.push(0); // 0为左区间下标初始位置
rightQue.push(nums.size() - 1); // nums.size() - 1为右区间下标初始位置
while (!nodeQue.empty()) {
TreeNode* curNode = nodeQue.front();
nodeQue.pop();
int left = leftQue.front(); leftQue.pop();
int right = rightQue.front(); rightQue.pop();
int mid = left + ((right - left) / 2);
curNode->val = nums[mid]; // 将mid对应的元素给中间节点
if (left <= mid - 1) { // 处理左区间
curNode->left = new TreeNode(0);
nodeQue.push(curNode->left);
leftQue.push(left);
rightQue.push(mid - 1);
}
if (right >= mid + 1) { // 处理右区间
curNode->right = new TreeNode(0);
nodeQue.push(curNode->right);
leftQue.push(mid + 1);
rightQue.push(right);
}
}
return root;
}538.把二叉搜索树转换为累加树
本题也不难,在 求二叉搜索树的最小绝对差 和 众数 那两道题目 都讲过了 双指针法,思路是一样的。
视频讲解:
这道题其实就是中序遍历(不过是改成了右中左)的时候修改一下遍历节点的值,所以只需要在遍历模板的基础上修改一下即可,迭代法也是同理——
class Solution {
private:
int pre = 0; // 记录前一个节点的数值
void traversal(TreeNode* cur) { // 右中左遍历
if (cur == NULL) return;
traversal(cur->right);
cur->val += pre;
pre = cur->val;
traversal(cur->left);
}
public:
TreeNode* convertBST(TreeNode* root) {
pre = 0;
traversal(root);
return root;
}
};总结篇
好了,二叉树大家就这样刷完了,做一个总结吧
注意——
-
涉及到二叉树的构造,无论普通二叉树还是二叉搜索树一定前序,都是先构造中节点。
-
求普通二叉树的属性,一般是后序,一般要通过递归函数的返回值做计算。
-
求二叉搜索树的属性,一定是中序了,要不白瞎了有序性了。
原文地址:https://blog.csdn.net/mrmobi/article/details/136009119
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_65897.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!