刷题日记
3.1 简单模拟
此类题型根据题目描述进行代码的编写,考察代码能力,刷题记录如下:
- B1001
- B1032
- B1016
- B1026
- B1046
- B1008
- B1012
- B1018
- A1042
- A1046
- A1065
- B1010
- A1002
- A1009
错题记录
B1008 数组元素循环右移问题
一个数组_A_中存有_N_(>0)个整数,在不允许使用另外数组的前提下,将每个整数循环向右移_M_(≥0)个位置,即将_A_中的数据由(_A_0_A_1⋯_AN_−1)变换为(_AN_−_M_⋯_AN_−1_A_0_A_1⋯_AN_−_M_−1)(最后_M_个数循环移至最前面的_M_个位置)。如果需要考虑程序移动数据的次数尽量少,要如何设计移动的方法?
输入格式:
每个输入包含一个测试用例,第1行输入_N_(1≤_N_≤100)和_M_(≥0);第2行输入_N_个整数,之间用空格分隔。
输出格式:
在一行中输出循环右移_M_位以后的整数序列,之间用空格分隔,序列结尾不能有多余空格。
思路分析:
1.出错点:需要注意题目中未说明m<n,m可能大于n
#include <bits/stdc++.h>
using namespace std;
int arr[110];
int main(){
int n,m;
scanf("%d %d",&n,&m);
m=m%n;
for(int i=1;i<=n;i++){
scanf("%d",&arr[i]);
}
for(int i=m-1;i>=0;i--){
printf("%d ",arr[n-i]);
}
for(int i=1;i<n-m;i++){
printf("%d ",arr[i]);
}
printf("%d",arr[n-m]);
return 0;
}
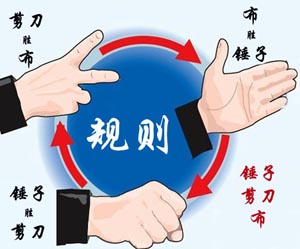
B1018 锤子剪刀布
大家应该都会玩“锤子剪刀布”的游戏:两人同时给出手势,胜负规则如图所示:
现给出两人的交锋记录,请统计双方的胜、平、负次数,并且给出双方分别出什么手势的胜算最大。
输入格式:
输入第 1 行给出正整数 N(≤105),即双方交锋的次数。随后 N 行,每行给出一次交锋的信息,即甲、乙双方同时给出的的手势。C 代表“锤子”、J 代表“剪刀”、B 代表“布”,第 1 个字母代表甲方,第 2 个代表乙方,中间有 1 个空格。
输出格式:
输出第 1、2 行分别给出甲、乙的胜、平、负次数,数字间以 1 个空格分隔。第 3 行给出两个字母,分别代表甲、乙获胜次数最多的手势,中间有 1 个空格。如果解不唯一,则输出按字母序最小的解。
输入样例:
10
C J
J B
C B
B B
B C
C C
C B
J B
B C
J J
输出样例:
5 3 2
2 3 5
B B
思路分析:
1.本题容易出错的关键在于使用scanf("%c")的时候,%c会读入空格和换行,需要使用getchar()读入多余的换行符n,我是在打印读入的符号的时候发现的,当时想到这一方面的原因是因为我一开始使用了函数帮助我判断谁赢了,但是函数传回的参很奇怪,所以才往这一方向尝试,后来才想到这一点。
2.优化的点:
- 本题是循环相克的顺序,因此存在
(k1+1)%3==k2这一方式判断输赢 - 可以把字母转化为数字,会简单很多
#include <bits/stdc++.h>
using namespace std;
int jia[3],yi[3];
int l1[128],l2[128];
int main(){
int n;
char a,b;
scanf("%d",&n);
getchar();
while(n--){
scanf("%c %c",&a,&b);
getchar();
if(a=='C'&&b=='J'||a=='J'&&b=='B'||a=='B'&&b=='C'){
jia[0]++;
yi[2]++;
l1[a]++;
}else if(a=='C'&&b=='C'||a=='J'&&b=='J'||a=='B'&&b=='B'){
jia[1]++;
yi[1]++;
}else if(a=='C'&&b=='B'||a=='J'&&b=='C'||a=='B'&&b=='J'){
jia[2]++;
yi[0]++;
l2[b]++;
}
}
printf("%d %d %dn",jia[0],jia[1],jia[2]);
printf("%d %d %dn",yi[0],yi[1],yi[2]);
char list[3]={'B','C','J'};
int max1=0,max2=0;
for(int i=0;i<3;i++){
char temp=list[i];
if(l1[temp]>max1){
a=temp;
max1=l1[temp];
}
if(l2[temp]>max2){
b=temp;
max2=l2[temp];
}
}
printf("%c %c",a,b);
return 0;
}
#include <bits/stdc++.h>
using namespace std;
int change(char x){
if(x=='B')
return 0;
if(x=='C')
return 1;
if(x=='J')
return 2;
}
int jia[3],yi[3];
int m1[3],m2[3];
int main(){
char list[3]={'B','C','J'};
int n;
scanf("%d",&n);
getchar();
char a,b;
int a_,b_;
while(n--){
scanf("%c %c",&a,&b);
getchar();
a_=change(a);
b_=change(b);
if((a_+1)%3==b_){
jia[0]++;
yi[2]++;
m1[a_]++;
}
if(a_==b_){
jia[1]++;
yi[1]++;
}
if((a_+2)%3==b_){
yi[0]++;
jia[2]++;
m2[b_]++;
}
}
printf("%d %d %dn",jia[0],jia[1],jia[2]);
printf("%d %d %dn",yi[0],yi[1],yi[2]);
int i1=0,i2=0;
for(int i=0;i<3;i++){
if(m1[i]>i1){
i1=m1[i];
a=list[i];
}
if(m2[i]>i2){
i2=m2[i];
b=list[i];
}
}
printf("%c %c",a,b);
return 0;
}
A1042 Shuffling Machine
前言:本题我虽然做出来了,但是在做的过程中我有参考答案,因此这道题的思路也记录一下。
#include <bits/stdc++.h>
using namespace std;
int main(){
int order[55];
int list1[55];
int list2[55];
char list_[5]={'S','H','C','D','J'};
int k;
scanf("%d",&k);
for(int i=1;i<=54;i++){
scanf("%d",&order[i]);
list1[i]=i;
}
while(k--){
for(int i=1;i<=54;i++){
list2[order[i]]=list1[i];
}
for(int i=1;i<=54;i++){
list1[i]=list2[i];
}
}
for(int i=1;i<=54;i++){
if(i!=1) printf(" ");
list1[i]--;
printf("%c%d",list_[list1[i]/13],list1[i]%13+1);
}
return 0;
}
思路分析:
1.这题与B1018 锤子剪刀布有一些类似,它们都有以下特点:存在一定顺序(B1018是循环相克顺序,本题是字母与序号存在顺序关系)->可以将字母统一转换为数字,方便计算
A1065 A+B and C (64bit)
前言:这题的解法我真是一点思路木有,属于是计组和数据结构的完美结合了,在下佩服;但如果要我硬写的话,我可能会用大数加减来解决这道题,但对这题来说有属于是稍微的杀鸡用牛刀了一些。
Given three integers A, B and C in (−263,263), you are supposed to tell whether A+B>C.
Input Specification:
The first line of the input gives the positive number of test cases, T (≤10). Then T test cases follow, each consists of a single line containing three integers A, B and C, separated by single spaces.
Output Specification:
For each test case, output in one line Case #X: true if A+B>C, or Case #X: false otherwise, where X is the case number (starting from 1). Each line should ends with ‘n’.
思路分析:
1.本题A B C的数据范围为[-2^63,2^63),需要用long long数据类型存储,但涉及到加法操作,一定会存在溢出的情况,即两个正数之和等于负数或两个负数之和等于正数。
2.溢出情况的分析,A+B的最大值是2^64-2,对应在long long数据类型变量中存储的值是(2^64-2)%2^64=-2,而A+B正溢出的取值范围易得[-2^63,-2],所以当A>0 B>0 A+B<0为正溢出,为true;反之,A+B的最小值是-2^64,存储值是-2^64%2^64=0,所以当A<0 B<0 C>=0为负溢出,为false。
3.值得注意的是,A+B溢出情况下,属于程序的未定义行为,此时的结果不一定是long long类型的,因此为了能够和C比较,我们需要把它存储在res中。
#include <bits/stdc++.h>
using namespace std;
int main(){
int t;
scanf("%d",&t);
for(int i=1;i<=t;i++){
long long a,b,c;
scanf("%lld %lld %lld",&a,&b,&c);
long long res=a+b;
bool flag;
if(a>0&&b>0&&res<0) flag=true;
else if(a<0&&b<0&&res>=0) flag=false;
else if(res>c) flag=true;
else if(res<=c) flag=false;
if(flag) printf("Case #%d: truen",i);
else printf("Case #%d: falsen",i);
}
return 0;
}
坑题记录
B1010 一元多项式求导
前言:本题虽然不难,但是我卡了许久,或许是因为太久没有接触数学微分了,求导都没意识到常数求导结果是0,以及一些意想不到的bug,故此记录一下本题。
设计函数求一元多项式的导数。(注:xn(_n_为整数)的一阶导数为_nxn_−1。)
输入格式:
以指数递降方式输入多项式非零项系数和指数(绝对值均为不超过 1000 的整数)。数字间以空格分隔。
输出格式:
以与输入相同的格式输出导数多项式非零项的系数和指数。数字间以空格分隔,但结尾不能有多余空格。注意“零多项式”的指数和系数都是 0,但是表示为 0 0。
#include <bits/stdc++.h>
using namespace std;
int arr[1005];
int main(){
int a,b;
int num=0;
while(scanf("%d %d",&arr[2*num+1],&arr[2*num+2])!=EOF){
num++;
}
int out=0;
for(int i=0;i<num;i++){
if(arr[2*i+2]==0&&num==1){
printf("0 0");
}else if(arr[2*i+2]==0&&num!=1){
continue;
}else{
if(out!=0) printf(" ");
out++;
printf("%d %d",arr[2*i+1]*arr[2*i+2],arr[2*i+2]-1);
}
}
return 0;
}
思路分析:
1.常数的导数是0,故对应的系数项和指数项都是0
2.特殊情况当无非零多项式的时候,需要输出0 0
3.当有非零多项式和常数项同时存在的时候,常数项不需要输出
扩展:指数乘法需要考虑数组长度变化
A1002 A+B for Polynomials
前言:本题思路正确,然鹅,坑点竟然是我之前看过但又没有仔细考虑的浮点数加减问题,所以特此记录一下浮点数坑点的相关知识。
浮点数加减:eps=1e-8== fabs(a-b)<eps 需要注意的是,fabs取绝对值非常重要,这也是我踩坑的原因> (a-b)>eps< (a-b)<-(eps)>= (a-b)>-(eps)<= (a-b)<(eps)
3.1 简单模拟 刷题总结 易错点分析
1.int long long类型变量的数据范围
int的数据范围是[-2^31,2^31-1],数量级范围为[-2*10^9,2*10^9]
long long的数据范围是[-2^63,2^63-1],数量级范围为[-9*10^18,9*10^18]
2.输出变量名错误,手误,复制粘贴的时候尤其容易犯这错误
3.边界情况的考虑B1008
4.字母与数字的转换,A1042和B1018的总结,如果涉及到字母和数字的结合处理,同时字母存在一定的规律,可以考虑把字母转换为数字,统一运算。
5.空格读入,在读入数字的时候其实不用考虑这一问题,但是当题目的输入有字符的时候,需要格外注意:
%c可以读入空格和换行符getchar()可以读入空格和换行符,常用于读取换行符,常见应用如下
输入样例
2
A B
scanf("%d",&n);
getchar();
scanf("%c %c",&a,&b);
getchar();
6.A1065题溢出情况
溢出的判定:正数相加得到负数,发生正溢出;负数相加得到正数,发生负溢出
溢出范围的确定:2^64-2(最大值)%
原文地址:https://blog.csdn.net/wawa_is_studying/article/details/136034041
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_66139.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!