船员投保的数学模型(MATLAB求解)

1.问题描述

劳动工伤事故，即我们平时所说的“工伤事故”，也称职业伤害，是指劳动者在生产岗位上，从事与生产劳动有关的工作中发生的人身伤害事故、急性中毒事故或职业病。船员劳动工伤事故是指船员在船舶生产岗位上，从事与船舶生产有关的作业(操作)中发生的可以认定为工伤的人身伤害事故，以及上、下船途中发生的人身伤害事故等.船员是船舶的核心和第一资源，船舶的各项工作都要依靠船员来完成。安全是船舶永恒的主题，人身安全更是各项安全工作的“第一要务”。船员的工伤事故一直萦绕着船舶的安全，且时有发生，不但影响船员的个人利益和船员的家庭幸福，而且影响船舶和企业的品牌和社会的声誉. 船员的工作具有较高的危险性, 因此研究船员工伤（劳工）、意外、医疗保险方案具有重要意义.

2.模型的假设

2.1船员的工伤损失模型

(1)不同岗位,不同年龄的船员发生各类工伤的概率不同

(2)各岗位各年龄的工资不同

(3)各类工伤的治疗费用和补偿费用不同

2.2保险公司的保费模型

(4)法规执行前后工作费用和利润不变

(5)法规执行后投保人数增加

(6)法规执行后增加的投保人中发生各类工伤的概率不大于法规执行前

MATLAB代码如下:

%% 保险模型的建立
clc;close all;clear all;%清除变量
% 年龄    在船人数    工伤人数    千人伤亡率
% <20    420    3    7.14
% 2l～25    4560    50    10.97
% 26～30    3720    34    9.14
% 3l～35    2940    48    16.33
% 36～40    2520    54    21.43
% 4l～45    2340    42    17.95
% 46～50    2220    61    27.48
% 51～55    1980    95    47.98
% 56～60    180    7    38.89
%% 伤亡的年龄段
CasualtyAge={‘<20′,’2l～25′,’26～30′,’3l～35′,’36～40′,’4l～45′,’46～50′,’51～55′,’56～60’};
CasualtyAgeValue=[18,20;
    21,25;
    26,30;
    31,35;
    36,40;
    41,45;
    46,50;
    51,55;
    56,60];
%% 伤亡的年龄均值
CasualtyAgeValue=mean(CasualtyAgeValue,2);
%% 各个年龄段的伤亡比例
CasualtyRateForAge=[7.14
    10.97
    9.14
    16.33
    21.43
    17.95
    27.48
    47.98
    38.89]/1000;

CasualtyRateForAge
%% 各种类型的伤亡比例
CasualtiesType={‘轻伤’,’重伤’,’死亡和失踪’};
CasualtiesRateForType=[178
    4
    36];
CasualtiesRateForType=CasualtiesRateForType./sum(CasualtiesRateForType)

%% 各种伤亡的损失
long1=length(CasualtyRateForAge);
long2=length(CasualtiesRateForType);
P=15;%单位万
LostForAgeDie=(60-CasualtyAgeValue)*P;%年龄段的损失
LostForAgeAndType=zeros(long1,long2);
W=[1,10];%受伤医疗费用,单位万元
n=[1,2];%受伤年限
PForAgeAndType=zeros(long1,long2);%概率
for i=1:long1%年龄段
    for j=1:long2%类型
        switch j
            case {1,2}%轻伤和重伤
                LostForAgeAndType(i,j)=W(j)+n(j)*P;
            case 3%死亡和失踪
                LostForAgeAndType(i,j)=(60-CasualtyAgeValue(i))*P;%年龄段的损失=工资损失
        end
        PForAgeAndType(i,j)=CasualtyRateForAge(i)*CasualtiesRateForType(j);
    end
end
LostForAgeAndType
PForAgeAndType
% PForAgeAndType=PForAgeAndType./sum(sum(PForAgeAndType))

%% 员工侧的总损失的数学期望如下
LostAll=sum(sum(LostForAgeAndType.*PForAgeAndType))

%% 保险公司赔偿标准
DisposableIncome=2.9547;% 2013年度全国城镇居民人均可支配收入,单位万
Reparation=[27,0.9;%1
    25,0.85;%2
    23,0.8;%3
    21,0.75;%4
    18,0.7;
    16,0.6;
    15,0;
    13,0;
    11,0;
    9,0];%10级  第一列是直接补偿,第二列是间接补偿=伤残津贴 ,以月工资为基数
DeathCompensation=20;%死亡和失踪的赔偿年数
%% 计算保险公司支付的费用的数学期望
%% 简化:1-4级为重伤,5-10级为轻伤,且各级均等
PForAgeDegree=zeros(long1,11);%每一级工伤对应的概率
CompensationValue=zeros(long1,11);%每一年龄每一级工伤的赔偿期望
for i=1:long1%年龄段
    for j=1:11%类型
        switch j
            case {1,2,3,4}%重伤
                PForAgeDegree(i,j)=PForAgeAndType(i,2)/4;%对应概率
                CompensationValue(i,j)=((60-CasualtyAgeValue(i))*Reparation(j,2)*P+Reparation(j,1)*P/12)*PForAgeDegree(i,j);%赔偿
            case {5,6,7,8,9,10}%轻伤
                PForAgeDegree(i,j)=PForAgeAndType(i,1)/6;%对应概率
                CompensationValue(i,j)=((60-CasualtyAgeValue(i))*Reparation(j,2)*P+Reparation(j,1)*P/12)*PForAgeDegree(i,j);%赔偿
            case {11}%死亡和失踪
                PForAgeDegree(i,j)=PForAgeAndType(i,3)/1;%对应概率
                CompensationValue(i,j)=((DisposableIncome*DeathCompensation)+6*P/12)*PForAgeDegree(i,j);%赔偿
        end
    end
end

PForAgeDegree
CompensationValue

t1=[‘船员侧损失的数学期望=’,num2str(LostAll),’万元’];
disp(t1);

t1=[‘保险公司侧理赔的数学期望=’,num2str(sum(sum(CompensationValue))),’万元’];
disp(t1);
 

MATLAB计算过程

各个年龄段的死亡比例 :

    0.0071

    0.0110

    0.0091

    0.0163

    0.0214

    0.0180

    0.0275

    0.0480

    0.0389

各个工伤种类占工伤的比例

    0.8165

    0.0183

    0.1651

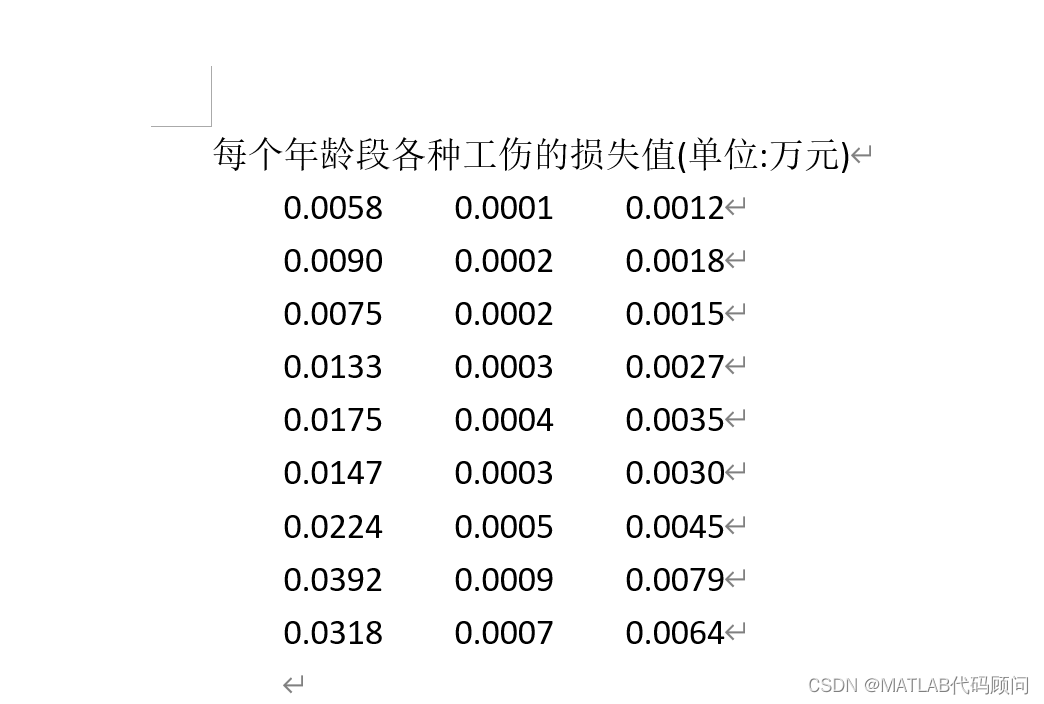
每个年龄段各种工伤的损失值(单位:万元)

    16    40   615

    16    40   555

    16    40   480

    16    40   405

    16    40   330

    16    40   255

    16    40   180

    16    40   105

    16    40    30

每个年龄段各种工伤的损失值(单位:万元)

    0.0058    0.0001    0.0012

    0.0090    0.0002    0.0018

    0.0075    0.0002    0.0015

    0.0133    0.0003    0.0027

    0.0175    0.0004    0.0035

    0.0147    0.0003    0.0030

    0.0224    0.0005    0.0045

    0.0392    0.0009    0.0079

0.0318    0.0007    0.0064

代码007普通

打赏 收藏 海报 链接