1.题目
输入一个
n
n
n 行
m
m
m列的整数矩阵,再输入
q
q
q 个操作,每个操作包含五个整数
x
1
,
y
1
,
x
2
,
y
2
,
c
x1,y1,x2,y2,c
x1,y1,x2,y2,c,其中
(
x
1
,
y
1
)
(x1,y1)
(x1,y1) 和
(
x
2
,
y
2
)
(x2,y2)
(x2,y2)表示一个子矩阵的左上角坐
标和右下角坐标。
每个操作都要将选中的子矩阵中的每个元素的值加上
c
c
c。
请你将进行完所有操作后的矩阵输出。
输入格式
第一行包含两个整数
n
n
n 和
m
m
m。
第二行包含
n
n
n 个整数,表示整数序列。
接下来
m
m
m 行,每行包含三个整数
l
,
r
,
c
l,r,c
l,r,c,表示一个操作。
输出格式
共 n 行,每行 m个整数,表示所有操作进行完毕后的最终矩阵。
数据范围
1
≤
n
,
m
≤
1000
,
1≤n,m≤1000,
1≤n,m≤1000,
1
≤
q
≤
100000
,
1≤q≤100000,
1≤q≤100000,
1
≤
x
1
≤
x
2
≤
n
,
1≤x1≤x2≤n,
1≤x1≤x2≤n,
1
≤
y
1
≤
y
2
≤
m
,
1≤y1≤y2≤m,
1≤y1≤y2≤m,
−
1000
≤
c
≤
1000
,
−1000≤c≤1000,
−1000≤c≤1000,
−
1000
≤
矩阵内元素的值
≤
1000
−1000≤矩阵内元素的值≤1000
−1000≤矩阵内元素的值≤1000
输入样例:
3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1
输出样例:
2 3 4 1
4 3 4 1
2 2 2 2
2.基本思想
前缀和的逆运算
如果扩展到二维,我们需要让二维数组被选中的子矩阵中的每个元素的值加上
c
c
c,是否也可以达到
O
(
1
)
O(1)
O(1)的时间复杂度。答案是可以的,考虑二维差分。
a
[
]
[
]
a[][]
a[][]数组是
b
[
]
[
]
b[][]
b[][]数组的前缀和数组,那么
b
[
]
[
]
b[][]
b[][]是
a
[
]
[
]
a[][]
a[][]的差分数组
原数组:
a
[
i
]
[
j
]
a[i][j]
a[i][j]
我们去构造差分数组:
b
[
i
]
[
j
]
b[i][j]
b[i][j]
使得
a
a
a数组中
a
[
i
]
[
j
]
a[i][j]
a[i][j]是
b
b
b数组左上角
(
1
,
1
)
(1,1)
(1,1)到右下角
(
i
,
j
)
(i,j)
(i,j)所包围矩形元素的和。
如何构造
b
b
b数组呢?
我们去逆向思考。
同一维差分,我们构造二维差分数组目的是为了 让原二维数组
a
a
a中所选中子矩阵中的每一个元素加上
c
c
c的操作,可以由
O
(
n
∗
n
)
O(n*n)
O(n∗n)的时间复杂度优化成
O
(
1
)
O(1)
O(1)
已知原数组
a
a
a中被选中的子矩阵为 以
(
x
1
,
y
1
)
(x1,y1)
(x1,y1)为左上角,以
(
x
2
,
y
2
)
(x2,y2)
(x2,y2)为右下角所围成的矩形区域;
始终要记得,
a
a
a数组是
b
b
b数组的前缀和数组,比如对
b
b
b数组的
b
[
i
]
[
j
]
b[i][j]
b[i][j]的修改,会影响到
a
a
a数组中从
a
[
i
]
[
j
]
a[i][j]
a[i][j]及往后的每一个数。
假定我们已经构造好了
b
b
b数组,类比一维差分,我们执行以下操作
来使被选中的子矩阵中的每个元素的值加上
c
c
c
b[x1][y1] += c;
b[x1,][y2+1] -= c;
b[x2+1][y1] -= c;
b[x2+1][y2+1] += c;
每次对b数组执行以上操作,等价于:
for(int i=x1;i<=x2;i++)
for(int j=y1;j<=y2;j++)
a[i][j]+=c;
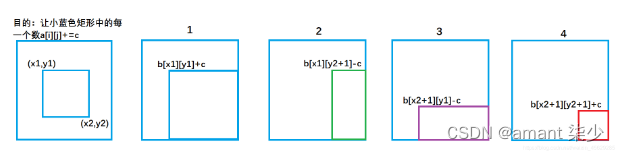
我们画个图去理解一下这个过程:

b[x1][ y1 ] +=c ; 对应图1 ,让整个a数组中蓝色矩形面积的元素都加上了c。
b[x1,][y2+1]-=c ; 对应图2 ,让整个a数组中绿色矩形面积的元素再减去c,使其内元素不发生改变。
b[x2+1][y1]- =c ; 对应图3 ,让整个a数组中紫色矩形面积的元素再减去c,使其内元素不发生改变。
b[x2+1][y2+1]+=c; 对应图4,让整个a数组中红色矩形面积的元素再加上c,红色内的相当于被减了两次,再加上一次c,才能使其恢复。
我们将上述操作封装成一个插入函数:
void insert(int x1,int y1,int x2,int y2,int c)
{ //对b数组执行插入操作,等价于对a数组中的(x1,y1)到(x2,y2)之间的元素都加上了c
b[x1][y1]+=c;
b[x2+1][y1]-=c;
b[x1][y2+1]-=c;
b[x2+1][y2+1]+=c;
}
我们可以先假想a数组为空,那么b数组一开始也为空,但是实际上a数组并不为空,因此我们每次让b数组以(i,j)为左上角到以(i,j)为右下角面积内元素(其实就是一个小方格的面积)去插入 c=a[i][j],等价于原数组a中(i,j) 到(i,j)范围内 加上了 a[i][j] ,因此执行n*m次插入操作,就成功构建了差分b数组.
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
insert(i,j,i,j,a[i][j]); //构建差分数组
}
}
总结

3.代码实现
import java.util.Scanner;
public class Main {
static int N = 1010;
static int[][] a = new int[N][N], b = new int[N][N];
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(), m = sc.nextInt(), q = sc.nextInt();
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
a[i][j] = sc.nextInt();
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
insert(i, j, i, j, a[i][j]);
while (q-- > 0) {
int x1 = sc.nextInt(), y1 = sc.nextInt(), x2 = sc.nextInt(), y2 = sc.nextInt(), c = sc.nextInt();
insert(x1, y1, x2, y2, c);
}
//二维前缀和
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
b[i][j] += b[i][j - 1] + b[i - 1][j] - b[i - 1][j - 1];
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
System.out.print(b[i][j] + " ");
}
System.out.println();
}
}
private static void insert(int x1, int y1, int x2, int y2, int c) {
b[x1][y1] += c;
b[x2 + 1][y1] -= c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y2 + 1] += c;
}
}
原文地址:https://blog.csdn.net/qq_51251599/article/details/135974010
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_66563.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!