1-3 动手学深度学习v2-线性回归的从零开始实现-笔记

手动创建训练数据集

根据带有噪声的线性模型构造一个人造数据集。我们使用线性模型参数

w

=

[

2

,

−

3.4

]

T

pmb{w} = [2,-3.4]^{T}

w=[2,−3.4]T、

b

=

4.2

b = 4.2

b=4.2和噪声项

ϵ

epsilon

ϵ生成数据集及其标签：

y

=

X

w

+

b

+

ϵ

pmb{y} = pmb{Xw}+b+epsilon

y=Xw+b+ϵ

%matplotlib inline # 在plot的时候，默认嵌入到notebook里面
import random # 随机梯度下降/随机初始权重 会用到
import torch
from d2l import torch as d2l # torch的一些模版

# 生成 y = Xw + b + 噪声
def synthetic_data(w, b, num_examples):     
    X = torch.normal(0, 1, (num_examples, len(w)))
    # 均值为0，标准差为1的随机数，样本数（行数）为num_examples，列数为列向量w的行数
    y = torch.matmul(X, w) + b 
    # y = Xw + b
    y += torch.normal(0, 0.01, y.shape)
    # 为了让问题难一点，我们引入了随机噪声，均值为0，标准差为0.01，矩阵形状长的和y一样，效果也就是在y现有基础上，每个位置上的元素加上随机初始化的噪声值
    return X, y.reshape((-1, 1))
    #返回数据样本矩阵X，标签向量y

true_w = torch.tensor([2, -3.4]) # 这个人造数据集真实的w
# 创建一个列向量
true_b = 4.2 # 这个人造数据集真实的b
features, labels = synthetic_data(true_w, true_b, 1000)
# 相当于是创建了1000个样本，每个样本有两个特征，这些所有的样本的真实w和b为上述，同时也引入了随机噪声

print('feature:', features[0], 'nlabel:', labels[0])
# 输出第0个样本的特征和标签，即具体样本值长什么样，就是X，即对应的标签是多少，即y

y.reshape((-1, 1))这行代码在Python中通常用于NumPy数组或类似的数据结构，其目的是改变数组y的形状（shape）。这里的reshape方法用于给数组一个新的形状，而不改变其数据。

• -1在reshape方法中被用作一个特殊值，它表示该维度的大小应该被自动计算，以便保持数组中元素的总数不变。换句话说，-1可以被理解为“自动推断出的大小”。相当于我最后只要得到一个列向量就可以，具体有多少行，我一开始并不关心，直接先用-1替代，自动帮我算好就行。
• (1)表示新的形状应该有一个列，这意味着你想将数组y转换成一个列向量。
• 总结一下，y.reshape((-1, 1))的作用是将y转换为一个列向量。如果y原本是一个一维数组，这个操作会使其变成一个二维数组，其中有多行但只有一列。

上述代码输出结果：

feature: tensor([-1.3127, -1.2715]) # 第0个样本的两个特征 （列向量）
label: tensor([5.8931]) # 它对应的标签值

plot出来看一下：

d2l.set_figsize()
d2l.plt.scatter(features[:,1].detach().numpy(),labels.detach().numpy(),1);
# 把特征的第一列（所有样本的第二个特征）拿出来     把标签拿出来，即y
# detach是指在python的一些版本中需要把它从pytorch的计算图中detach分离出来（但仍指向原始数据），才能通过.numpy()转成numpy数组，这是为了避免绘图操作影响梯度计算。
# scatter 绘制散点图
# x坐标：特征的第一列（所有样本的第二个特征） 
# y坐标：标签值，即y
# 最后的参数1可能指的是散点的大小。在matplotlib的scatter函数中，可以通过s参数指定点的大小。如果这里的1确实意在控制点的大小，那么它指的是使用很小的点来绘图。

# 这行代码的作用是：使用features的第二个特征和labels作为坐标，绘制一个散点图，其中每个点的大小为1。这可以帮助可视化特征与标签之间的关系，是数据分析和机器学习中常用的一种方法。

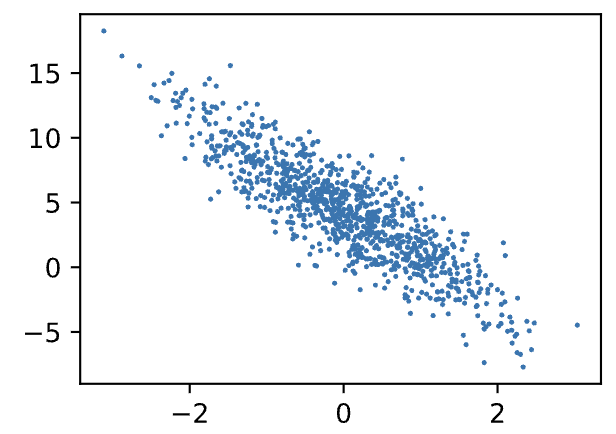
我们可以看出，人造的数据集是具有线性相关性的。

实现随机抽取指定批量大小的样本的方法

定义一个data_iter函数，该函数接受批量大小、特征矩阵和标签向量作为输入，生成大小为batch_size的小批量。

def data_iter(batch_size, features, labels):
    num_examples = len(features) # 从特征矩阵的行数中得到样本数
    indices = list(range(num_examples)) # 生成每个样本的索引 0-n-1 再转成python list
    # 这些样本是随机读取的，没有特定的顺序
    random.shuffle(indices) # 把生成的索引list（即indices）的元素顺序完全打乱 这样我后面就可以用一个随机的顺序去访问样本
    for i in range(0, num_examples, batch_size): # 从0开始，到num_examples结束，步长为batch_size
        batch_indices = torch.tensor(indices[i:min(i + batch_size,num_examples)])
        # 从i开始，到min(i + batch_size,num_examples)结束，
        # 一般情况下就是i～i + batch_size，只有i + batch_size超出样本总数了，才会用到num_examples
        yield features[batch_indices], labels[batch_indices] # yield 返回

batch_size = 10

for X, y in data_iter(batch_size, features, labels):
    print(X, 'n', y)
    break

在这段代码中，yield关键字的作用是把data_iter函数变成一个生成器（generator）。
生成器是一种特殊的迭代器，它允许你逐步产生（生成）值，而不是一次性返回所有值。使用yield的好处是它可以在每次产生一批数据时，暂停函数的执行，等到下一次迭代请求时再继续，从而节省内存并允许实时处理数据。
运行一下，输出是：

tensor([[-2.7191e-01,  4.7745e-01],
        [ 9.1430e-01,  1.3391e+00],
        [ 1.1257e+00,  1.4340e+00],
        [ 4.5012e-01, -7.8356e-01],
        [ 6.7112e-01,  1.1518e-03],
        [ 1.2587e+00, -4.4198e-01],
        [ 5.3823e-01,  1.7816e-01],
        [ 5.5030e-01,  2.0622e-01],
        [-4.2540e-01,  8.0550e-01],
        [ 7.9017e-01, -1.3217e+00]]) 
 tensor([[ 2.0360],
        [ 1.4640],
        [ 1.5675],
        [ 7.7668],
        [ 5.5319],
        [ 8.2097],
        [ 4.6658],
        [ 4.6141],
        [ 0.6039],
        [10.2707]])

由输出结果可知，我们成功实现了从总样本特征矩阵中随机抽取一个指定batch_size大小的小批量样本及其标签。

定义初始化模型参数

# 将w随机初始化为一个均值为0，标准差为0.01的，大小为2行1列，requires_grad=True表示我们需要计算梯度
w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True)
# 将偏差b初始化为0，requires_grad=True表示我们需要计算梯度
b = torch.zeros(1, requires_grad=True) 

定义模型

def linreg(X, w, b):
    # 线性回归模型
    return torch.matmul(X, w) + b

定义损失函数

def squared_loss(y_hat, y):
    # 均方损失
    return (y_hat - y.reshape(y_hat.shape))**2 / 2
    # 虽然按理来说，y_hat和y应该元素个数一样，但是可能一个是行向量，一个是列向量，这里把他们统一成一样的，
    # 这样就可以直接在y和y_hat之间进行元素对元素的操作了，比如计算差值或者逐元素的乘法。
    
    # 这里没有作均值 没有除以样本总数
    # 我自己理解这里为什么没有除以样本总数，总结来说有几点：
    # 1. 作者不想让这个函数多一个样本数量这一传入参数
    # 2. 这里是将y_hat和y按位相减，然后再把差值平方，再除以二分之一，仔细看看，这里算出来的其实是一个列向量，而不是一个标量，
    # 其实就是算出来y的每一位的平方，还没有求和的操作，这是放到最后‘训练过程’中完成。
    # 3. 损失值后面是要求导用的，我们思考一下，被求导的这个数，它乘或除一个常数，这个常数是会一直跟着它的，不会丢掉。
    # 所以，这里少了一个除法算平均的过程，但是放到算导数（即梯度）的时候，记得除一下，也不迟，这里不除，还能让函数显得更简洁。

定义优化算法

def sgd(params, lr, batch_size):
# params 参数的list，包括w和b
# lr 学习率
    # 小批量随机梯度下降
    with torch.no_grad():     # 不需要计算梯度（更新的时候不要参与梯度计算）
        for param in params:  # 对参数里的每一个参数
            param -= lr * param.grad / batch_size  # 这里写batch_size其实是在算均值  param.grad参数的梯度
            param.grad.zero_() # 手动把梯度设置成0，下一次计算梯度的时候就不会和这次相关了

为什么更新的时候不要参与梯度计算？

在参数更新时不参与梯度计算的原因是为了避免更新过程中对参数梯度的计算。当我们使用梯度下降法更新参数时，我们的目的是根据当前梯度来调整参数值，以最小化损失函数。这一过程应该是一个简单的数学操作，不应该被视为模型的一部分或影响模型的梯度计算图。

如果在参数更新时允许计算梯度，那么更新操作本身（如param -= lr * param.grad / batch_size）会被认为是模型的一部分，并且会影响后续梯度的计算，这显然是我们不希望的。因此，使用torch.no_grad()上下文管理器暂时禁用梯度计算，确保这一更新操作不会影响到计算图和后续梯度的计算。

为什么需要手动地把梯度设置成0？

在PyTorch中，梯度是累加的。这意味着每次调用.backward()时，计算得到的梯度会被加到已存在的梯度上。这样设计是出于计算效率和便利性的考虑，特别是在需要计算复杂表达式导数时。然而，这也意味着在每次进行参数更新之前，我们需要手动将梯度清零，以防止梯度信息在不同批次之间相互干扰。（这里是在参数更新之后清零，其实也是一个意思）

如果不将梯度归零，则每次执行.backward()时，梯度会在原有的基础上累加，导致每一批数据的梯度不是基于其自身的损失计算的，而是包含了前面所有批次的梯度信息，这将导致参数更新方向错误，严重影响模型训练的效果。

如何理解“在PyTorch中，梯度是累加的。这意味着每次调用.backward()时，计算得到的梯度会被加到已存在的梯度上”？

在PyTorch中，梯度累加的机制是指，当你对一个计算图中的张量调用.backward()方法时，得到的梯度不会替换掉张量当前的.grad属性值，而是会加上去。这个设计主要是为了方便在一些特定的场景下，比如在RNN（递归神经网络）的训练中，或者当你想要在一个批次中累加多个子批次（mini-batches）的梯度时。

这里是一个简单的例子来说明这个概念：

假设有一个参数张量param，其初始梯度（如果有的话）是0。当你第一次对某个损失函数loss1调用loss1.backward()时，param的梯度会根据loss1对param的导数被计算并存储在param.grad中。现在，如果你再次对另一个损失函数loss2调用loss2.backward()而没有在这两次调用之间手动清零param.grad，那么loss2对param的导数就会加到param.grad上，而不是替换它。

为什么需要梯度累加？

梯度累加提供了一种灵活的方式来处理不同的训练需求，比如：

• 内存限制：对于非常大的模型或非常大的输入数据，可能没有足够的内存一次性处理整个批次的数据。在这种情况下，可以将一个大的批次分成几个小批次，分别计算每个小批次的梯度，并让它们累加起来，最后进行一次参数更新。
• 不同来源的梯度：在一些复杂的模型训练中，可能希望从不同的损失函数或数据集中累积梯度，然后基于累积的梯度进行一次参数更新。

训练过程

lr = 0.03
num_epochs = 3  # 把整个数据扫三遍
net = linreg    # 模型
loss = squared_loss # 均方损失

for epoch in range(num_epochs): # 遍历轮次
    for X, y in data_iter(batch_size, features, labels): # 拿出一个批量大小的X和y
        l = loss(net(X, w, b), y)  # 把X，w，b放进模型做预测，然后和标签值y算出损失
        # l的行数为批量大小，列数为1，l是向量，不是标量
        l.sum().backward() # l中的所有元素被加到一起求和，然后求梯度 l.sum()这才是损失函数的值，也即损失值的平方和
        sgd([w,b], lr,batch_size) # 利用梯度对w和b进行更新。
        # 这里的batch_size不是特别对的 因为万一样本数不能整除batch_size，最后一块可能不足batch_size的大小
    # 对数据扫完一遍后，我们来评估一下进度，而且评估的操作是不需要计算梯度的，所以我们把它放在no_grad里面
    with torch.no_grad():
        train_l = loss(net(features, w, b), labels) # 用完整的特征矩阵评估损失
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}') 
        # 把损失print出来，因为上面定义的损失函数计算中没有算平均数，所以这里要手动调用mean算一下

控制台输出结果：

epoch 1, loss 0.031483
epoch 2, loss 0.000118
epoch 3, loss 0.000053

我们可以看到，随着轮次的增大，损失在越来越小。

比较真实参数和通过训练学到的参数来评估训练的成功程度：

print(f'w的估计误差：{true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差：{true_b - b}')

控制台输出结果：

w的估计误差：tensor([-9.6321e-05, -6.9380e-05], grad_fn=<SubBackward0>)
b的估计误差：tensor([0.0006], grad_fn=<RsubBackward1>)

可以看到真实参数和通过训练学到的参数的差距已经越来越小了。

调整超参数的取值，看看效果如何

将学习率从0.03调整为0.001

（需要重新初始化

w

pmb{w}

w和

b

b

b，这样就可以不会跟着上一次的梯度结果来了，因为如果

w

pmb{w}

w和

b

b

b没变，那么梯度会一直累加）

控制台输出：

epoch 1, loss 13.930480
epoch 2, loss 11.320221
epoch 3, loss 9.199821

我们发现，当学习率特别小的时候，过了3轮epoch，损失值还是特别大。

我们可以增大轮次再看看，将epoch改为10，重新初始化

w

pmb{w}

w和

b

b

b，再跑一遍。
控制台输出：

epoch 1, loss 13.925218
epoch 2, loss 11.315891
epoch 3, loss 9.196276
epoch 4, loss 7.474352
epoch 5, loss 6.075387
epoch 6, loss 4.938728
epoch 7, loss 4.015125
epoch 8, loss 3.264555
epoch 9, loss 2.654557
epoch 10, loss 2.158751

我们可以看到，跑了10个epoch之后，损失还是很大，不如我们之前正常学习率的效果。

将学习率从0.03调整为10

（需要重新初始化

w

pmb{w}

w和

b

b

b，这样就可以不会跟着上一次的梯度结果来了，因为如果

w

pmb{w}

w和

b

b

b没变，那么梯度会一直累加）
控制台输出如下：

epoch 1, loss nan
epoch 2, loss nan
epoch 3, loss nan
epoch 4, loss nan
epoch 5, loss nan
epoch 6, loss nan
epoch 7, loss nan
epoch 8, loss nan
epoch 9, loss nan
epoch 10, loss nan

我们发现，当学习率太大的时候，求导的时候可能会除0，或者有无限的值出现，会让loss变成not a number。

备注

该模型计算损失的时候是这样的：

def squared_loss(y_hat, y):
    # 均方损失
    return (y_hat - y.reshape(y_hat.shape))**2 / 2
    # 虽然按理来说，y_hat和y应该元素个数一样，但是可能一个是行向量，一个是列向量，这里把他们统一成一样的，
    # 这样就可以直接在y和y_hat之间进行元素对元素的操作了，比如计算差值或者逐元素的乘法。
    
    # 这里没有作均值 没有除以样本总数

并没有算平均损失，即没有除去样本总数，在这里其实是没有影响的，因为它在后面计算梯度的时候，是这样的：

def sgd(params, lr, batch_size):
# params 参数的list，包括w和b
# lr 学习率
    # 小批量随机梯度下降
    with torch.no_grad():     # 不需要计算梯度（更新的时候不要参与梯度计算）
        for param in params:  # 对参数里的每一个参数
            param -= lr * param.grad / batch_size  # 这里写batch_size其实是在算均值  param.grad参数的梯度
            param.grad.zero_() # 手动把梯度设置成0，下一次计算梯度的时候就不会和这次相关了

而且这里的方法，其实不是对线性回归模型的忠实实现，更多的是对小批量随机梯度下降法的忠实实现。

也可以这么解释：乘除常数的效果，是会伴随着梯度的计算的，不会因为梯度的计算而消失。所以我当初计算损失的时候忘记除了，在梯度下降的时候记得除一下，也是一样的（前面忘了，后面补上），而且，其实这里李沐老师是刻意让自己写的损失函数，不受到样本数量的影响，从而他刻意不在前面除，留到后面除。
而且损失函数那边也除了也“不对”，因为损失函数那边始终算出来的是一个向量，并没有去计算平方和，而是放到训练的过程中去计算损失的平方和，然后再合理的在优化算法里面去补一下前面漏的除法操作。

代码007普通

打赏 收藏 海报 链接