本文介绍: Redis集合简介。集合基本命令saddsmemberssismemberscardspopsrandmembersmovesrem集合间操作sintersinterstoresunionsdiffsdiifstore
挑战自己,每天进步一点点,成就将属于不停止脚步的你。
目录
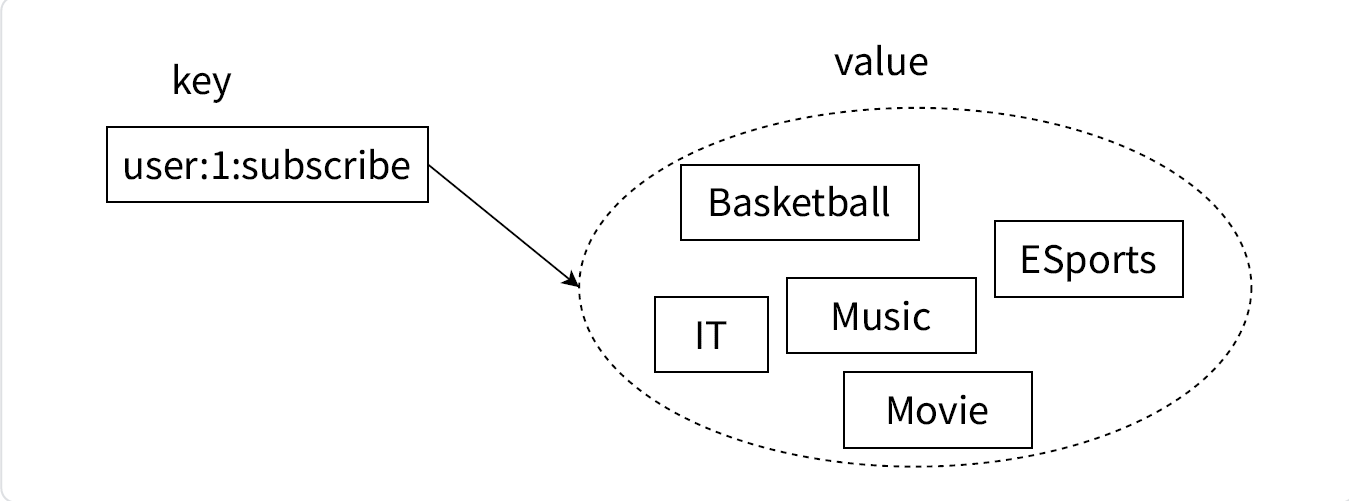
Redis集合?
集合基本命令
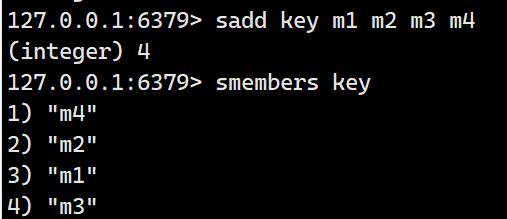
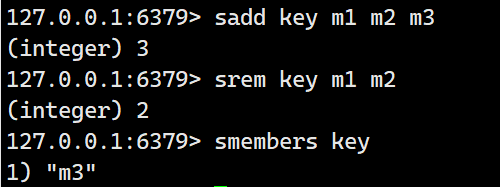
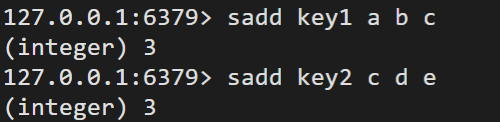
sadd
smembers
sismember
scard
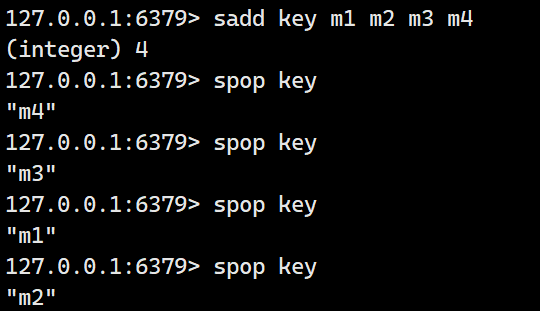
spop
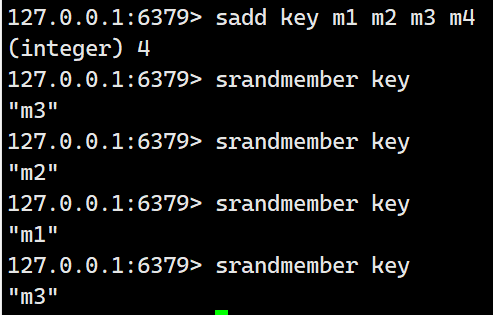
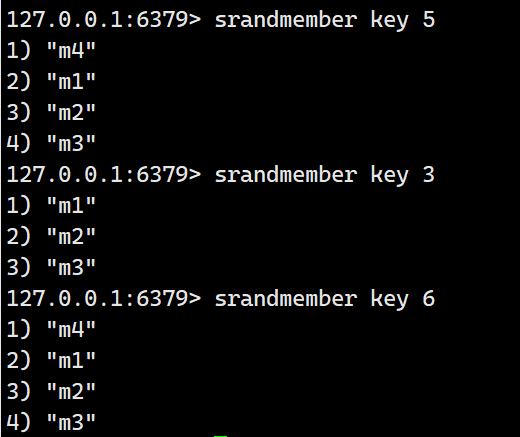
srandmember
smove
srem
集合间操作
sinter
sinterstore
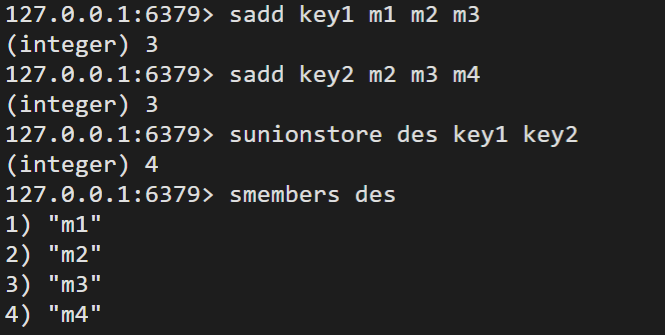
sunion
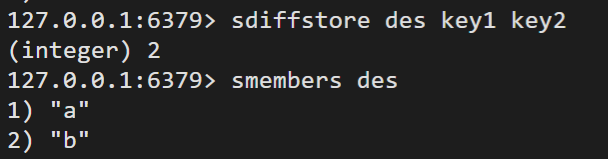
sdiff
sdiifstore
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。